前言

本文为GAMES101现代计算机图形学入门 的学习笔记系列。

我们的系列笔记将分为两部分：

1. 课堂笔记
2. 作业

原课程为2020年2月闫令琪所教授的 GAMES101 现代计算机图形学入门。

课程主页：https://sites.cs.ucsb.edu/~lingqi/teaching/games101.html
（幻灯片和课程录像均在此处）

课程共计22节。作业共计8次。

针对人群：计算机图形学入门新手

教材：
Steve Marschner and Peter Shirley的"Fundamentals of Computer Graphics"
第三版或更新版本。目前无官方中文版。
民间翻译：https://www.stubbornhuang.com/1812/

笔记目录

---

2022-6-6

本节阅读：第 8 章（The Graphics Pipeline）, 第 8.2.3 节；第 9 章（Signal Processing）

注：本文没有按照课堂所讲的顺序，而是按照我理解的逻辑顺序。

正文

本节内容：

• 抗锯齿
  – 采样

锯齿（Jaggies）

在上节光栅化中，我们定义了一个inside函数，只要在三角形内部，我们就认定其为1，即涂成红色，否则就认为是0，不涂成红色。

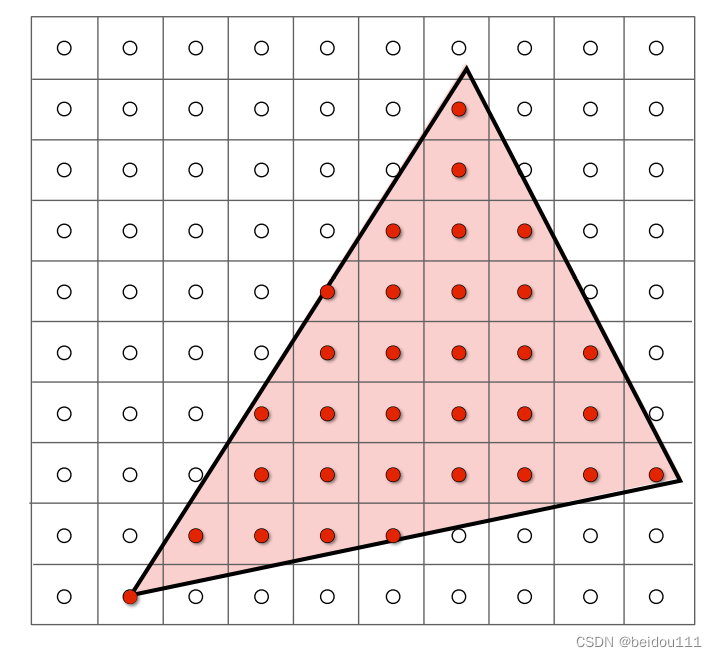
这样会造成一个问题：

• 在三角形边缘处，会出现锯齿（jaggies）

所谓锯齿，就是下图这种，如同阶梯状的小格子

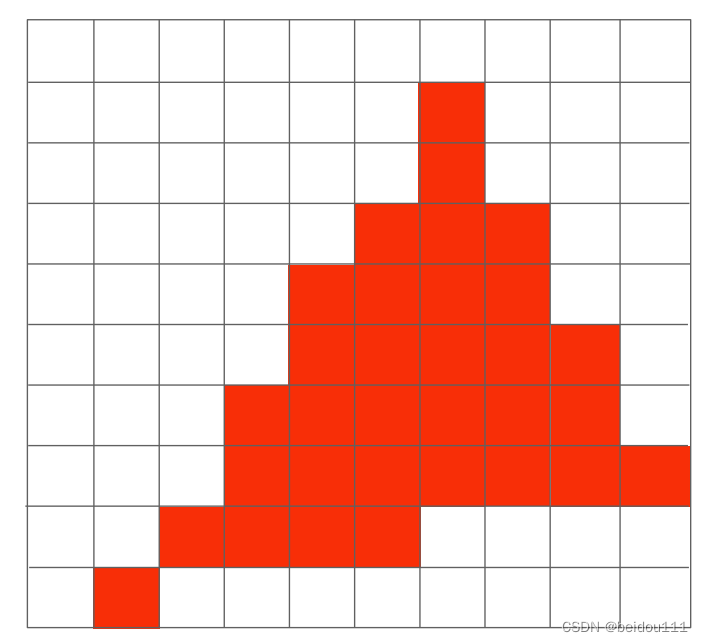
一种显而易见的抗锯齿的方法，就是增加分辨率。

显然，我们像素约密约多，锯齿就约难以察觉。

然而这就意味着我们要更换我们的显示器。比如原本你是1080P的显示器，现在升级成4K的，当然锯齿就会少很多了。然而这种更换硬件的办法，是要加钱的。我们能不能再不升级硬件的条件下，减少锯齿呢？

有的！那就是增加模糊。

如图，虽然三角形的边缘模糊了，但是边缘上的锯齿也看不见了。

对我们的人眼来说，模糊有时会比锯齿感觉好一些。

这当然不是免费的午餐，它有两个缺点：

• 变模糊了
• 需要额外的计算量

我们本节就讲：如何将其变模糊从而达到抗锯齿？

在此之前，我们先认识一下走样。

走样(Aliasing)

上面说到的锯齿其实只是走样的一种，也还有许多其他的走样。

所谓采样，其实就是对连续信息的离散化。 无所谓这是时间上的连续信息，还是空间上的连续信息。简单来说：采样=离散化

• 摩尔纹
  摩尔纹（Moire）也是一种走样。
  在许多软件（比如photoshop）中，先把图片改小，再把它缩放到原来的尺寸，就会造成下面这种现象。实际上，这是因为把许多像素值给抽掉了（例如抽掉奇数行和基础列，图片的分辨率会变为原来的1/4），损失掉了许多原有信息。造成的结果，就是会出现摩尔纹。
  
• 车轮幻觉（Wagon Wheel Illusion）
  我们观察高速运行的车轮，或者电风扇，有时会发现上面的条纹像是在缓慢地倒转。这是因为我们的眼睛跟不上车轮的转速了。也就是人眼的时间采样率比实际的频率要小，造成了许多信息的损失。
  

这里就能看出：
走样的原因在于采样的频率跟不上信号的频率

采样定理（奈奎斯特定理/ 香农采样定理）

前面说，走样的原因在于采样的频率跟不上信号的频率。也就是如下图所示。由于采样点过于稀疏，根据采样点重构出来的曲线与原始的曲线完全不一致。

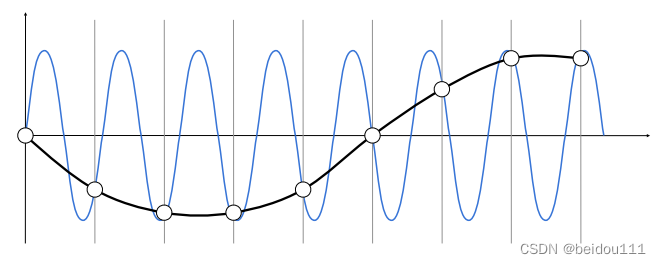
信息在采样的过程中完全地损失掉了。

显然，要让信息不损失，需要让采样频率高一些。高到什么程度呢？有如下定理。即采样定理，又被称为奈奎斯特定理或香农采样定理。

Nyquist在1924年第一个发现了该定理，而1948年香农明确地将其作为定理并加以解释。

采样定理陈述为：

当采样频率fs.max大于信号中最高频率fmax的2倍时(fs.max>2fmax)，采样之后的数字信号完整地保留了原始信号中的信息

超采样抗走样（Super-Sampling Anti-Aliasing）

既然问题在于采样率不够，那么我们就人为地增加采样率。但是记住前面提到过，我们不能在硬件层面上增加采样率，所以我们只能在软件层面上做一些工作。

其中最简单的一种方法就是超采样技术。更具体地说，我们要介绍的z只是其中的一种，叫多重采样技术（Multi-Sampling Anti-Aliasing, MSAA）。

其核心思想在于：将一个像素拆成nxn个。

例如拆成2x2个

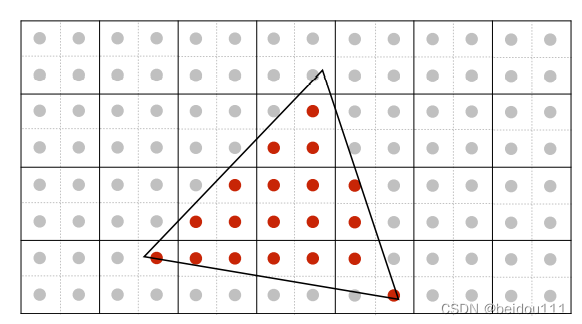
之前说到过，硬件条件不变，也就是一个像素只能是一种颜色的小色块。但是我们可以让其数值按比例进行变化。

例如，原本只是覆盖了一部分的边缘区域像素，我们现在可以让其值变为原来的75%，或25%。

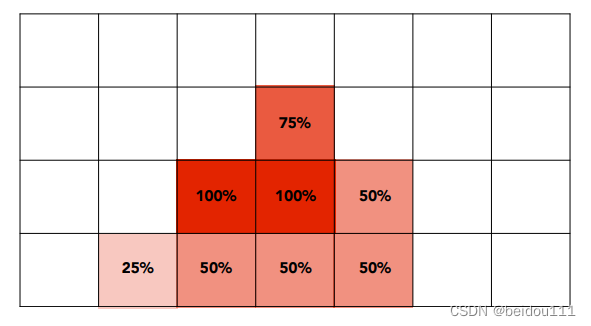
这样，我们就做到了边缘模糊的效果。

显然nxn的n值越大，我们得到的模糊效果越好。但是显然计算量会增加。

但是值得声明的是，实际的算法会采取一些更节约算力的办法，计算量的增幅不是简单的nxn倍。但是为了保持课程的简单，我们就不深究了。

以上便是本节课的主要内容之一了。

---

先模糊再采样 vs. 先采样再模糊

实际上，我们还有一个问题没有说，那就是：

必须按照顺序：先模糊，再采样。

假如先采样再模糊，会导致不但有锯齿，而且还模糊！

如下图所示

左边是先采样再模糊：结果是不但模糊了，还有锯齿！
右边是先模糊再采样：结果是锯齿消除了！

为什么会这样呢？

解答这个问题并不容易。

这就要涉及到信号处理的知识了。

下面的知识，假如学过信号处理，就会认为简单。假如没学过，就会觉得很难。

图像也是一种信号

首先，我们要理解：图像也是一种信号！

在我们的通常印象中，信号大概是一堆正弦余弦波，例如下面这样子。

但实际上，我们可以把图像也看成一种信号！

怎么看呢？

我们知道，图像其实就是一堆数字。每组数字表示了一个像素里的颜色值。

我们就可以认为这堆数字就是采样之后得到的采样点。但是请注意：这里不是在时间上采样了，而是在空间上采样。我们把这堆数字一个个地串联起来，其实也能画成一个波的样子。

但是信号是无限延伸的呀？没关系，我们就把图像不断地复制就好了。比如，认为往右边界继续走，就又循环到了图片的最左边。上下也同理。

傅里叶变换：时域与频域的互相转换

下面，我们介绍大名鼎鼎的傅里叶变换。

我们只要先记住：傅里叶变换其实就是个转换器，它将时域信号转换为频域信号。

相应地，也有逆傅里叶变换。就是把频域信号转换为时域信号。

为什么呢？以及什么是时域信号，什么是频域信号？

而为了理解这些，我们必须先介绍傅里叶展开（或者叫傅里叶级数）。

傅里叶展开

傅里叶发现：
任何周期函数都能写成正弦函数/余弦函数的叠加

这正是傅里叶展开。

例如，我们可以将一个方波表示为一系列不同频率和赋值的余弦波的叠加。

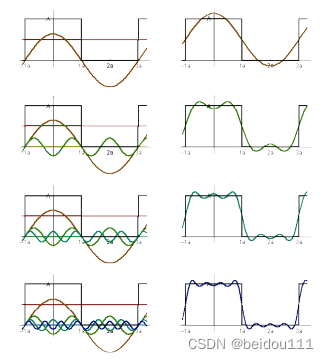
把这句话用数学语言描述出来就是

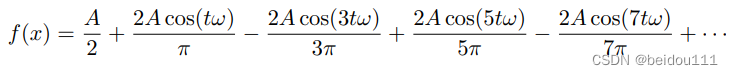
观察上面的式子，我们发现重要的信息有两个：

1. 各个余弦函数的幅值，也就是各项的系数
2. 各个余弦函数的频率，也就是cos函数括号内的系数。
   （PS: 严格来说应该叫角频率，频率乘以2$\pi$就是角频率）

幅值分别是
$2A/\pi ,-2A/3\pi ,2A/5\pi ,...$
角频率分别是
$w,3w,5w,...$

关键在于：重要的信息就只有这两组数字。

也就是除了幅值和频率，其他的一切都不重要。

换句话说，只要给我们一组幅值和频率，我们完全可以重构出原来的函数。

这样，我们就能用一组幅值和频率，等价于任意的周期函数。也就是任意的信号。

看到了吗？本来是一个连续的信号，我们只需要用一组离散的数字就能表示出来了。
（虽然这组数字是无限延伸的，但是很小的值我们完全可以忽略掉）

在上百年的实践中，我们也确实这样做了。我们把离散后这组数字，称之为频域信号。

时域与频域

给我们一组幅值和频率，我们其实可以把它画成一幅图。横坐标是频率，纵坐标是幅值。它是一个只有点的图。为了好看，我们把它画出柱子。这样的图，我们称之为频谱图。（spectrogram）

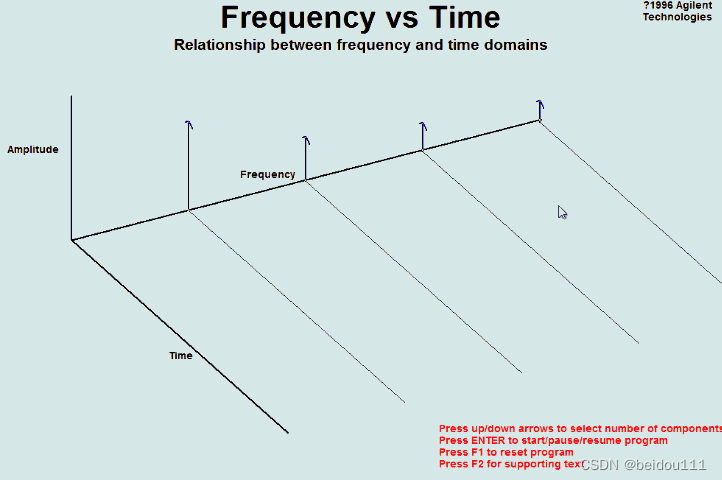
借助频谱图，我们完全可以将时域图画出来。

频域与时域之间的转换，借助的就是傅里叶变换。

傅里叶变换，其实就是转换公式。

图中的F函数，就是把原本时域的f函数变换为频域的F函数。即傅里叶变换公式。

图中的f函数，就是把原本频域域的F函数变换为时域的f函数。即傅里叶逆变换公式。

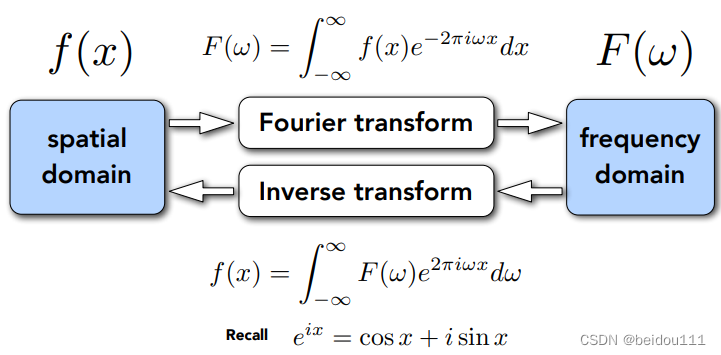
我们现在了解了，傅里叶变换其实就是一个转换器。那么，这样转换有什么意义呢？

其实意义就在于：滤波。

滤波

滤波就是把不想要的信息（比如噪声）给过滤掉。
（PS当然滤波滤掉的不一定是噪声，他还有许多用处）

在时域上滤波是不容易的，但在频域上非常容易。

我们想到，频域上，其实就是一组数字，也就是频率和幅值。我们把不想要的频率都删去，就是滤波。

首先，最简单的两种滤波器，是

• 高通滤波
• 低通滤波

高通滤波，顾名思义，就是只允许频率高于一定值的通过，而把其他的滤掉。

同理，低通滤波就是只允许低频的通过。

我们之前说过，图像其实也可以看成一种信号。

我们有这样一幅灰度图。他的每个像素值只是一个数，表示灰度的大小。灰度为0，就是白色，灰度为1，就是黑色。介于两者之间，就能显示明暗变化。
左图就是灰度图。我们称这是它的时域图。虽然它完全和时间没有关系。它是在空间上采样的。但是为了约定俗成，我们还是称之为时域图。实际上，我们也可以叫他为空域图（spatial domain），这样似乎更合理一些。

它经过傅里叶变换，可以转换为右边的频域图。

这张图可以这样看：它把频率最低的写在最中间。越往外，频率越高。用幅值表示灰度值。越是白点，表示幅值越大。

这样，我们可以做个高通滤波。把所有频率低的都删除掉。也就是如下

我们发现，高通滤波造成图片只保留了边缘。

这是为什么呢？

因为所谓的边缘（例如人物与背景的交界），其实在数值上是灰度值的急剧变换。可能在袖口处是完全的黑色，在背景则是完全的白色。这其实对应着高频率。（想象一下，频率高意味着信号波变化很急剧）所以高通滤波只保留了边缘。

那么低通滤波呢？

低通滤波，造成了模糊的效果。

这是因为，低通滤波相当于把数值变化很急剧的信号给删除掉了。当然就会造成模糊的效果。

那么即删除过高频率，又删除过低频率，只保留中间区域的频率，会是什么效果呢？
是如下效果

由此我们得知了：低通滤波就可以造成模糊的效果。

其实，我们还可以从另一种角度来看模糊，那就是卷积。

用卷积（平均）进行模糊

用卷积的方法可以造成模糊。

卷积

什么是卷积？

这点其实和CNN里面完全一致。就是设定一个小窗口，然后不断在小窗口内做乘法并求和。

如图所示，学过机器学习的同学一定很熟悉，这里就不多讲了。

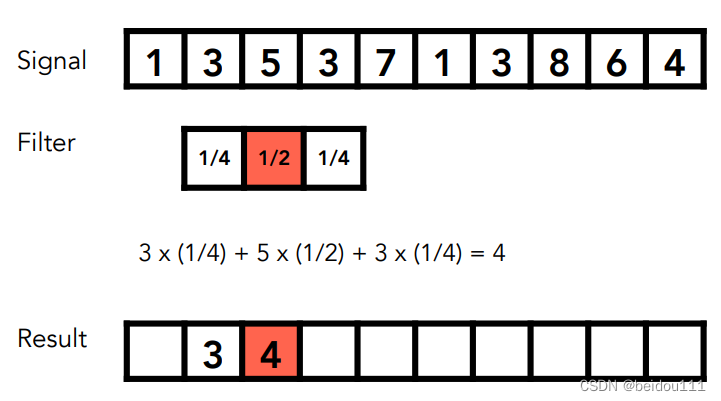
为什么要做卷积呢？因为卷积其实就是一种平均。平均当然会把边缘周围的像素值给模糊掉。

卷积定理：用傅里叶变换加速卷积

我们固然可以直接在原图像上做卷积，这不过是做一些加法乘法罢了。但是这样做卷积有个问题，那就是计算量很大。
但是人们发现，在频域上做卷积计算量是大大减少的。而且人们还发现，在时域上做卷积和再频域上做卷积，完全不影响结果。这就是卷积定理。

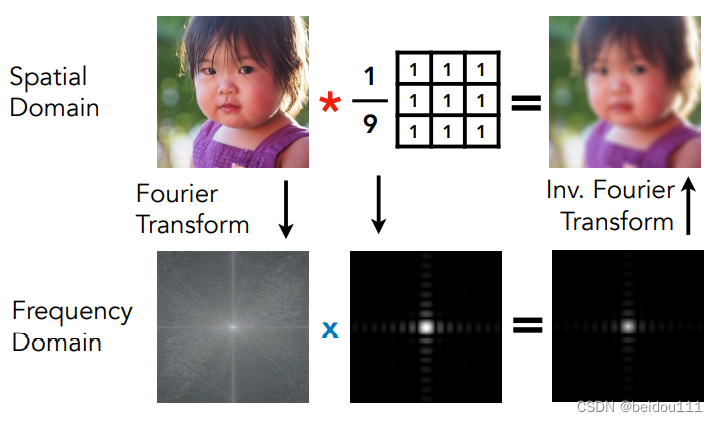
卷积定理指出，函数卷积的傅里叶变换是函数傅里叶变换的乘积。

于是，我们将图像先转化为频域，然后对其做卷积，最后再转换回空域，那么就得到了模糊的图像。

通过这样的来回转换，原本算法复杂度为n^2，现在可以减少到nlogn。

滤波与卷积

滤波与卷积，其实完全是一回事。

比如我们定义如下一个卷积核。做滤波。

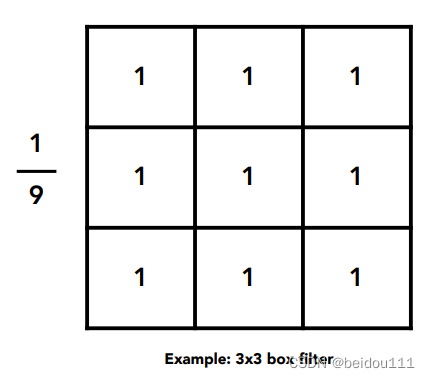
它和用一个方块进行滤波的结果是完全一致的。

从信号的角度看走样

我们现在补充完了所有的信号处理知识，可以回过头来看当初的问题了：

为什么先模糊再采样和先采样再模糊不一样？

那么我们就要先说一说，从信号的角度看，什么是走样呢？

我们观察如下的频域图

记住：频域图的横坐标是频率。所以信号采样率越高，信号波之间的相距越远！

假如采样点之间相距过近，就会造成信号之间的交叉。如图所示。重叠的部分造成了走样。

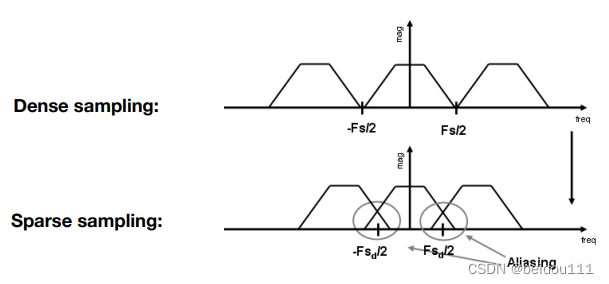
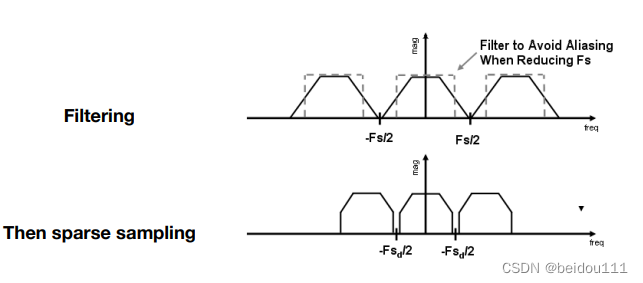
消除它的方法，就是提前把重叠的部分删掉。也就是如下所示。
（我们无法提高采样率，采样率是由设备的分辨率决定的）

最后

以上就是威武跳跳糖为你收集整理的【GAMES101】课堂笔记6--光栅化（深度测试与抗锯齿）前言正文的全部内容，希望文章能够帮你解决【GAMES101】课堂笔记6--光栅化（深度测试与抗锯齿）前言正文所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。