注:每一步可能依赖于上一步import的模块
一、数组
1,用numpy对数组进行运算
from numpy import array
mm=array((1, 1, 1))
pp=array((1, 2, 3))
则pp+mm 输出 array([2,3,4])
pp*2 array([2,4,6])
pp**2 array([1,4,9])
2,访问数组元素
pp[1]
输出2
3,多维数组
jj = array([[1, 2, 3], [1, 1, 1]])
注:上面这句话的意思是创建下面这样一个多维数组
jj =
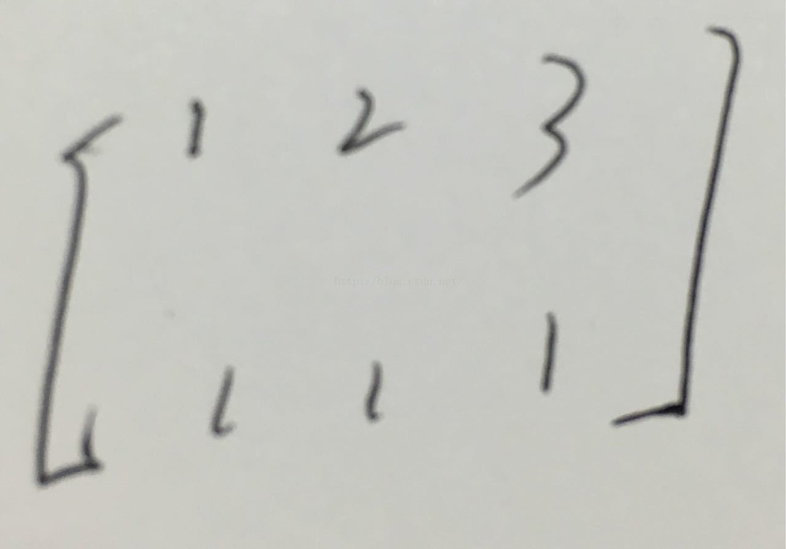
获取该数组元素:jj[0][1] 第一行第二列元素
输出2
用矩阵方式访问该元素:jj[0, 1]
输出2
4, 两个数组相乘:
>>> a1=array([1, 2, 3])
>>> a2=array([0.3, 0.2, 0.3])
>>> a1*a2
array([ 0.3, 0.4, 0.9])
>>> a1=array([1, 2, 3])
>>> a2=array([0.3, 0.2, 0.3])
>>> a1*a2
array([ 0.3, 0.4, 0.9])
二、矩阵
1,创建矩阵两种方式
>>> from numpy import mat, matrix
方法一:>>> ss=mat([1, 2, 3])
>>> ss
matrix([[1, 2, 3]])
方法二:>>> mm=matrix([1,2,3])
>>> mm
matrix([[1, 2, 3]])
2,访问矩阵元素:
>>> mm[0, 1]
2
2,将列表转换成矩阵:
>>> pyList = [5, 11, 1605]
>>> mat(pyList)
matrix([[ 5, 11, 1605]])
3,矩阵转置后再相乘:
>>> mm*ss.T
matrix([[14]])
>>> mm
matrix([[1, 2, 3]])
>>> ss.T
matrix([[1],
[2],
[3]])
4,查看矩阵是几行几列的:
>>> from numpy import shape
>>> shape(mm)
(1, 3)
>>> shape(ss.T)
(3, 1)
5,矩阵元素相乘:mm的每个元素和ss的每个元素相乘
>>> mm
matrix([[1, 2, 3]])
>>> ss
matrix([[1, 2, 3]])
>>> from numpy import multiply
>>> multiply(mm, ss)
matrix([[1, 4, 9]])
6其他
排序:注意sort()排序后原数组已改变
>>> aa=mat([7, 8, 5])
>>> aa
matrix([[7, 8, 5]])
>>> aa.sort()
>>> aa
matrix([[5, 7, 8]])
排序并显示排序后的序号: 排序完之后原数组不变
>>> dd=mat([4, 5, 1])
>>> dd.argsort()
matrix([[2, 0, 1]])
求矩阵均值:
>>> dd.mean()
3.3333333333333335
显示矩阵的行列数:
>>> jj = mat([[1, 2, 3], [8, 8, 8]])
>>> shape(jj)
(2, 3)
事实证明多维数组和矩阵基本相同:
>>> qq = array([[1, 2, 3], [8, 8, 8]])
>>> shape(qq)
(2, 3)
取出矩阵第二行的元素:用行号和冒号
>>> jj[1, :]
matrix([[8, 8, 8]])
取出第一行的第1列和第2列的元素:
>>> jj[0, 0:2]
matrix([[1, 2]])
注: 范围0:2表示从 0 取到 1
关于NumPy更多
http://docs.scipy.org/doc/
最后
以上就是风中网络最近收集整理的关于python array list matrix_Python多维数组和矩阵的全部内容,更多相关python内容请搜索靠谱客的其他文章。








发表评论 取消回复