我是靠谱客的博主 腼腆帅哥,这篇文章主要介绍Educational Codeforces Round 37 E. Connected Components?(bfs+思路),现在分享给大家,希望可以做个参考。
题意:给出n个点,m条不存在的边(除了不存在的边其他边都存在),输出有多少个连通分量,以及每个连通分量里点的个数(从小到大)
首先是存图,2e5*2e5的图,而且边又经常用到,用邻接表肯定是不行的,二维map可以解决这个问题
然后是优化,一个连通分量中的点都在同一个集合里,由于是无向图,对于一个连通分量中的点,他们之间可能会连很多条边,但只需要一条边就能确定他们之间的关系,所以其他那么多条边都可以优化掉,利用bfs,每次把v删掉,然后看剩下所有没加入集合中的点是否与v有关系,有关系则加入一个集合里,再把这点删了,重复这个过程即可
#include<bits/stdc++.h>
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
const int N=200005;
map<int,bool>e[N];
vector<int>mp,ans;
int bfs(int v)
{
int cnt=0;
queue<int>Q;
Q.push(v);
while(!Q.empty())
{
int u=Q.front();
Q.pop();
cnt++;
for(int i=0;i<mp.size();i++)
{
v=mp[i];
if(!e[u][v])
{
swap(mp[i],mp.back());
mp.pop_back();
--i;
Q.push(v);
}
}
}
return cnt;
}
int main()
{
int n,m,x,y;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)mp.push_back(i);
for(int i=1; i<=m; i++)
{
scanf("%d%d",&x,&y);
e[x][y]=1;
e[y][x]=1;
}
while(!mp.empty())
{
int v=mp.back();
mp.pop_back();
int x=bfs(v);
if(x)
ans.push_back(x);
}
sort(ans.begin(),ans.end());
printf("%dn",ans.size());
for(int i=0;i<ans.size();i++)
printf("%d ",ans[i]);
puts("");
}最后
以上就是腼腆帅哥最近收集整理的关于Educational Codeforces Round 37 E. Connected Components?(bfs+思路)的全部内容,更多相关Educational内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。
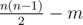 edges. Instead of giving you the edges that exist in the graph, we give you
edges. Instead of giving you the edges that exist in the graph, we give you 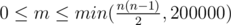 ).
).







发表评论 取消回复