图的遍历-拓扑排序

参考：https://blog.csdn.net/qq_35644234/article/details/60578189

问题描述：修一门课程之前必须修完该课程的先修课程，给出一个可行的选课顺序。（可能会有几种不同方案）

以上问题可以抽象为如下有向无环图的拓扑排序结果：

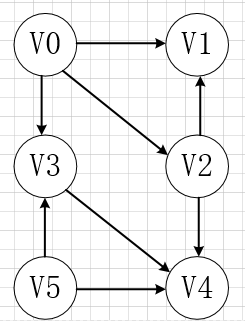
上图的邻接表为：

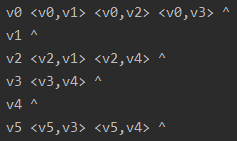
1、概念

拓扑排序（topological sort），将一个有向无环图（Directed Acyclic Graph，DAG）中所有顶点在不违反先决条件关系的前提下排成线性序列的过程称为拓扑排序。

先决条件，对于有向无环图G=(V,E)，从顶点到顶点之间有一条路径，则在序列中顶点必须在之前。

2、算法

法一：

从图中选择任意一个入度为0的顶点输出；从图中删掉该顶点及其所有的出边，并将出边对应顶点的入度减一；重复以上过程直到所有顶点都被遍历过。（假设无环）

法二：

深度优先搜索；逆序。

3、代码实现

# include <stack>
# include <string>
# include <iostream>
# include "string.h"
using namespace std;
struct AdjcNode {
int index; //保存弧尾顶点在顶点表中的下标
AdjcNode* next; //下一个关联的边
};
struct Vnode {
string data; //顶点名称，从v0开始
AdjcNode* first_adjcN; //第一个依附在该顶点的边
};
class Graph {
private:
int num_vertex; //图的顶点数量
int num_edge; //图的边数
int* indegree; //图中每个顶点的入度
Vnode* adjc_t; //邻接表
public:
Graph(int, int);
~Graph();
bool judgeEdgeValid(int, int);
void createGraph();
void printAdjcT();
bool topologicalSort();
bool topologicalSortByDFS();
void dfs(int n, bool* &visit, stack<string>& result);
};
Graph::Graph(int num_vertex, int num_edge) {
this->num_vertex = num_vertex;
this->num_edge = num_edge;
this->adjc_t = new Vnode[this->num_vertex];
this->indegree = new int[this->num_vertex];
for (int i = 0; i < this->num_vertex; ++i) {
this->indegree[i] = 0;
this->adjc_t[i].first_adjcN = NULL;
this->adjc_t[i].data = "v" + to_string(i);
}
}
Graph::~Graph() {
AdjcNode *p, *q;
for (int i = 0; i < this->num_vertex; ++i) {
if (!this->adjc_t[i].first_adjcN) continue;
p = this->adjc_t[i].first_adjcN;
while (p) {
q = p->next;
delete p;
p = q;
}
}
delete [] this->adjc_t;
delete [] this->indegree;
}
// 判断每次输入的边的信息是否合法。顶点从0开始编号
bool Graph::judgeEdgeValid(int start, int end) {
if (start<0 || end<0 || start>=this->num_vertex || end>=this->num_vertex) return false;
return true;
}
void Graph::createGraph() {
int start, end;
cout << "输入每条起点和终点的顶点编号（从0开始编号）" << endl;
for (int cnt = 0; cnt < this->num_edge; ++cnt) {
cin >> start;
cin >> end;
while (!this->judgeEdgeValid(start, end)) {
cout << "输入顶点不合法，请重新输入" << endl;
cin >> start;
cin >> end;
}
++this->indegree[end];
AdjcNode* temp = new AdjcNode;
temp->index = end;
temp->next = NULL;
if (this->adjc_t[start].first_adjcN == NULL) {
this->adjc_t[start].first_adjcN = temp;
this->adjc_t[start].data = "v" + to_string(start);
}
else {
AdjcNode* cur = this->adjc_t[start].first_adjcN;
while (cur->next) {
cur = cur->next;
}
cur->next = temp;
}
}
}
void Graph::printAdjcT() {
cout << "图的邻接矩表为：" << endl;
for (int cnt = 0; cnt < this->num_vertex; ++cnt) {
cout << this->adjc_t[cnt].data << " ";
AdjcNode* temp = this->adjc_t[cnt].first_adjcN;
while (temp) {
cout << "<" << this->adjc_t[cnt].data << "," << this->adjc_t[temp->index].data << "> ";
temp = temp->next;
}
cout << "^" << endl;
}
}
bool Graph::topologicalSort() {
cout << "图的拓扑序列为：" << endl;
stack<int> stk;
int i;
for (i = 0; i < this->num_vertex; ++i) {
if (this->indegree[i] == 0) stk.push(i);
}
// 用于计算输出顶点的个数
int cnt = 0;
while (!stk.empty()) {
i = stk.top();
stk.pop();
cout << this->adjc_t[i].data << " ";
AdjcNode* temp = this->adjc_t[i].first_adjcN;
while (temp) {
if (--this->indegree[temp->index] == 0) stk.push(temp->index);
temp = temp->next;
}
++cnt;
}
if (cnt == this->num_vertex) {
cout << endl;
return true;
}
cout << "此图有环，无拓扑序列" << endl;
return false;
}
bool Graph::topologicalSortByDFS() {
stack<string> res;
int i;
bool* visit = new bool[this->num_vertex];
memset(visit, 0, this->num_vertex);
cout << "基于DFS的拓扑排序为：" << endl;
for (i = 0; i < this->num_vertex; ++i) {
if (!visit[i]) this->dfs(i, visit, res);
}
for (i = 0; i < this->num_vertex; ++i) {
cout << res.top() << " ";
res.pop();
}
cout << endl;
return true;
}
void Graph::dfs(int n, bool *& visit, stack<string> & result) {
visit[n] = true;
AdjcNode* temp = this->adjc_t[n].first_adjcN;
while (temp) {
if (!visit[temp->index]) dfs(temp->index, visit, result);
temp = temp->next;
}
result.push(this->adjc_t[n].data);
}
int main() {
int num_vertex, num_edge;
cout << "输入图的顶点个数和边的条数：" << endl;
cin >> num_vertex >> num_edge;
Graph graph1(num_vertex, num_edge);
graph1.createGraph();
graph1.printAdjcT();
graph1.topologicalSort();
graph1.topologicalSortByDFS();
system("pause");
return 0;
}

最后

以上就是粗犷哈密瓜为你收集整理的图的遍历-拓扑排序的全部内容，希望文章能够帮你解决图的遍历-拓扑排序所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。