最短路径-Dijkstra(迪杰斯特拉)算法最短路径-Dijkstra(迪杰斯特拉)算法

50 阅读 0 评论 33 点赞

我是靠谱客的博主火星上宝贝，最近开发中收集的这篇文章主要介绍最短路径-Dijkstra(迪杰斯特拉)算法最短路径-Dijkstra(迪杰斯特拉)算法，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

最短路径-Dijkstra(迪杰斯特拉)算法

网图的最短路：

最短路径，是指两顶点之间经过的边上权值之和最小的路径，并且我们称路径的第一个顶点是源点，最后一个顶点是终点

Dijkstra(迪杰斯特拉)算法：

概况：

按路径长度递增的次序产生的最短路径算法，通过一步步计算出路径之间顶点的最短路径，在此过程中都是基于已经求出的最短路径基础上，求得更远顶点的最短路径

思想：

设当前已经求得的最短路径边集为{MT}，当前最短路终点与相连点（不在MT中）的距离（与起点距离）集合为{WP}

每次都在WP中取与当前终点最近的一个点，将最短边L加入最短路径集{MT}，记此时新的终点为NewEnd

扫描不在最短路径中的所有点，如果 NewEnd+L<Dis(表示起点到当前扫描点的距离)，更新最短路

相似算法：

在最小生成树上用过类似思想，只不过最小生成树要求全部点都要连通

留个传送门：最小生成树-Prim(普里姆)算法

图解：

两个工具：

a.Path[MAX_SIZE]：记录路径，Path[i]是i的前驱，路径方向 Path[i] -> i

b.Short_Path[MAX_SIZE]：Short_Path[i] 表示从起点Start（不一定是0或者1）到 i 的最短路径大小

以下图为栗，v0为起点

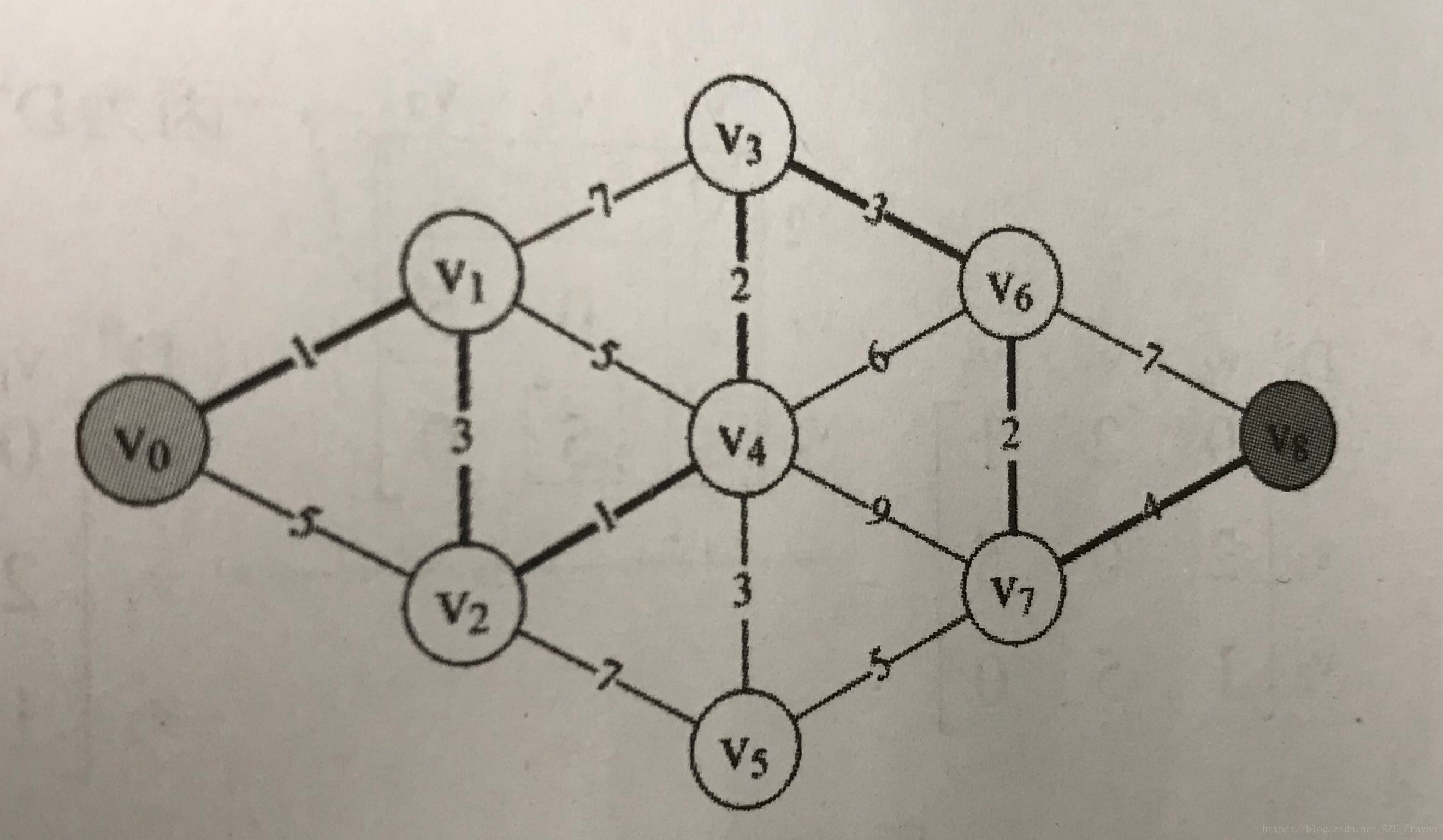
首先记录下v0到相连点的距离（明显是v1和v2），进行初始化，此时：

Path：{ 0 0 0 0 0 0 0 0 0 } --- 初始化0

Short_Path：{ 0 1 5 65535 65535 65535 65535 65535 65535 } --- v0与v1距离为1，v0与v2距离为5

选出最短Short_Path 中的最短距，v1成为新的最短路终点，如下图，此时v1与v2，v3，v4相连

所有v0-v3=1+7=8 .......，可得（扫描更新后）：

Path：{ 0 0 1 1 1 0 0 0 0 }

Short_Path：{ 0 1 4 8 6 65535 65535 65535 65535 }

一样，选出Short_Path中此时没有加入最短路顶点的最短路（红色），也就是4，得到 v0-v1-v2 ，v2为最短路新顶点

继续更新最短路，加入v4，v5，很明显，v0-v1-v4=6，而v0-v2-v4=5，路径更新为后者

Path：{ 0 0 1 1 2 2 0 0 0 }

Short_Path：{ 0 1 4 8 5 11 65535 65535 65535 }

此时没有加入最短路的最小路径为5，也就是v4作为新终点

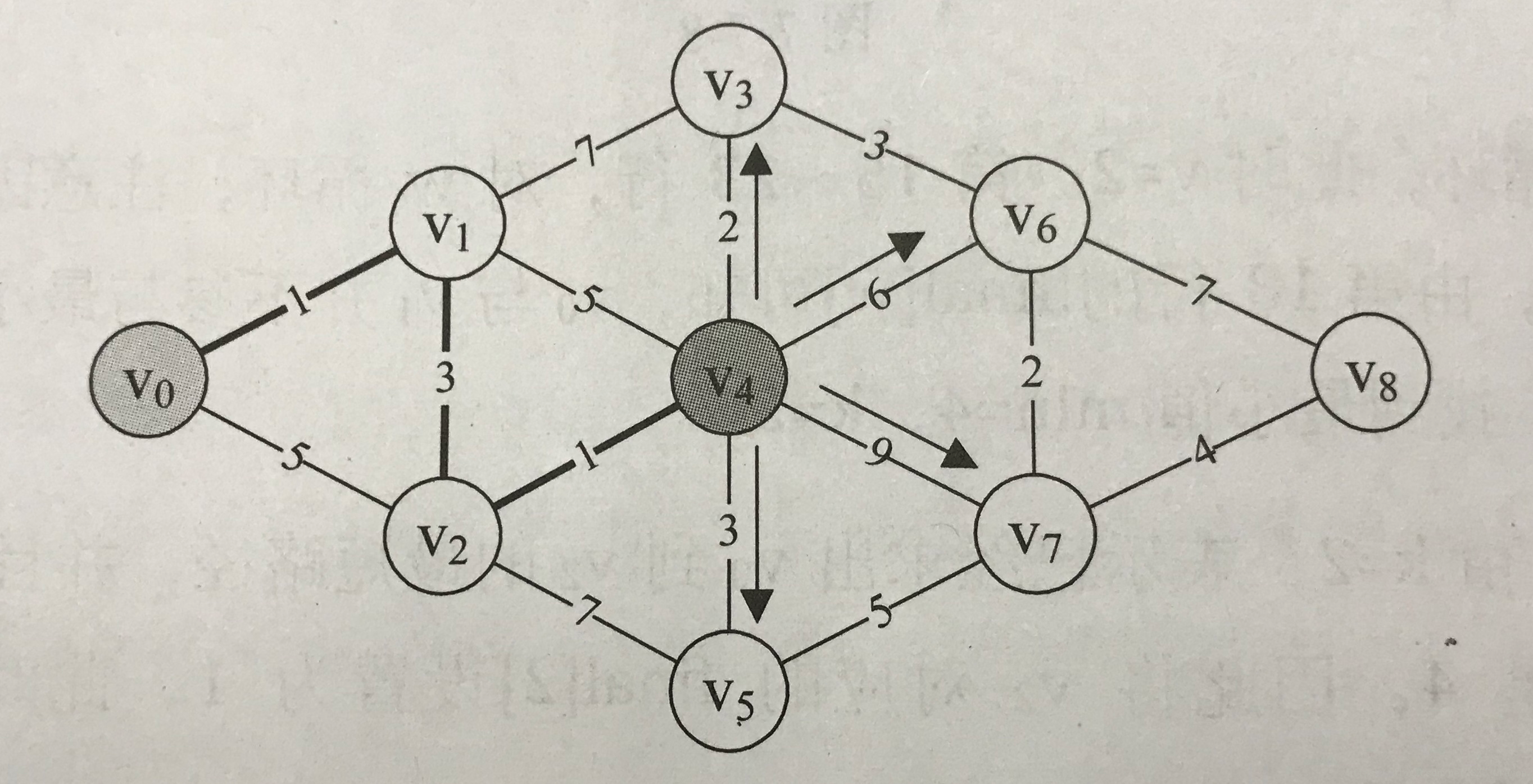
按之前步骤继续往下走，直到v8：

Path：{ 0 0 1 4 2 4 3 6 7 }

Short_Path：{ 0 1 4 7 5 8 10 12 16 }

如下图，得到最短路径：v0-v1-v2-v4-v3-v6-v7-v8，最短路长度为16

Short_Path的利用：

Short_Path 显然是每一次最短路径的延申，所以求得Start-End的最短路，同理，Start到任意点的最短路都可以在Short_Path 中查得

算法复杂度：

O（n^2）

Dijkstra模板：

#include <iostream>
#include<memory.h>
using namespace std;
#define MAX_SIZE 1024
#define INF 65535

//邻接图
struct MGrapth
{
    int Vexs[MAX_SIZE];  //顶点表
    int Arc[MAX_SIZE][MAX_SIZE];  //邻接矩阵
    int Num_Vertext,Num_Edges;  //顶点数，边数
};
MGrapth Map;

int Path[MAX_SIZE];   /*表示路径 Path[i]->i*/
int Short_Path[MAX_SIZE]; /*Start->i 的最短路径和*/
bool Vis[MAX_SIZE];   /*当前最短路径结点true*/
int Res;  /*最短路*/

void Init(int n,int m)
{
    Res=0;
    memset(Vis,0,sizeof(Vis));
    memset(Path,0,sizeof(Path));
    for(int i=0;i<=n;i++)
        for(int j=0;j<=m;j++)
            Map.Arc[i][j]=INF;
    Map.Num_Vertext=n;
    Map.Num_Edges=m;
}

void Dijkstra(int Start)
{
    int v,w,k,Min;
    for(v=0;v<Map.Num_Vertext;v++)
        Short_Path[v]=Map.Arc[Start][v];  /*Start到相连结点的距离*/

    Short_Path[Start]=0;   /*Start->Start 的距离为0*/
    Vis[Start]=1;   /*Start为当前最短路径结点*/

    for(v=1;v<Map.Num_Vertext;v++)
    {
        Min=INF;
        for(w=0;w<Map.Num_Vertext;w++)
        {
            if(!Vis[w]&&Short_Path[w]<Min)
            {
                k=w;
                Min=Short_Path[w];
            }
        }
        Vis[k]=true; /*找出最短路到散点的最小值，将该散点连入最短路*/

        for(w=0;w<Map.Num_Vertext;w++)  /*更新最短路*/
        {
            if(!Vis[w]&&Min+Map.Arc[k][w]<Short_Path[w])  /*图中某点到v0的距离比当前路短，更新*/
            {
                Short_Path[w]=Min+Map.Arc[k][w];
                Path[w]=k;
            }
        }
    }
}