Approximate Dynamic Programming（近似动态规划算法） Chapter 6 阅读笔记

前言

动态规划中的核心公式：
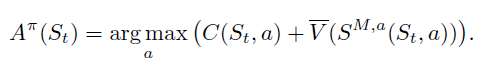可以理解为C表示MDP中的建立函数，S^(M,a)表示转移函数，A表示策略函数。

提示：以下是本篇文章正文内容，其中对相关术语翻译可能不太准确，请以英文为准，下面内容主要是作为个人阅读笔记，比较凌乱，仅供参考

一、Myopic Policies（贪婪策略）

Myopic Policies是指不使用对未来的预测信息，或者尝试对未来可能动作进行建模的策略。
其公式如下：

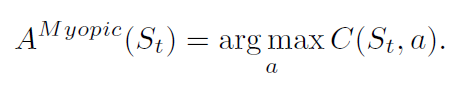
这里的C(St,a)表在状态St下执行a能够得到的奖励的多少。可以认为是自定义的奖励函数。因此Myopic Policies只是考虑了单步的信息，因此得到的累积奖励往往不会最优的。

二、Lookahead Policies(前视策略）

Loookahead Policies是通过考虑问题在未来的一些时间步长内的发展来进行优化，会具体对未来的状态和动作进行表示，这也是其和策略函数近似与价值函数近似的区别。

1.Tree search

Tree search方法是一种暴力搜索的方法，是指在当前状态下，通过枚举出未来T个时间段内所有可能的动作和状态，以及他们的奖励，来选在当前最合适的动作。这种方法只适用于动作空间和状态空间都比较小的情况下，而且一般T也不能太大。

2.Sparse sampling tree search

和Tree search策略不同的是，这种策略不需要完全枚举出所有的可能，而是通过蒙特卡洛采样方法来代替，采样次数一定多的时候，就有可能限制住误差。

3.Rollout heuristics

在动作空间非常大的情况下，前面树搜索的方法就不再适用。那么改进的一个思路就是，直接通过一些启发式的规则估计采取了一个动作后到达的状态的价值，而不是将采取一个动作后一定时间步长内所有的状态动作可能全都枚举出来。比如我们采取动作a，到达了状态A，那么从A开始通过一些启发式的规则（如myopic policies）仿真一定的步长估计出A的价值。如下式：

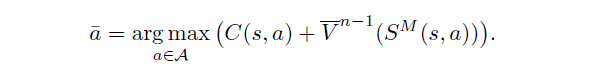
上式中，V^(n-1）就表示，通过myopic策略仿真一定步长估计状态价值的方法。这种策略的优点是简单且快速，而且这种用myopic policy去估计一个状态的价值的方法，比仅仅只用myopic的方法要好一点。

4.Rolling horizon procedures

前面的方法，都是适用于离散的动作空间（比如枚举动作，或者求argmax函数都限定了离散的动作空间）。
假设我们在状态St的时候，能够求解出t到t+H时间范围内的最优解，决策是at。那么我们应用at，就可以进入下一个状态St+1，然后重复得到t+1到t+1+H时间范围内的最优解。这种方法因此称为Rolling horizon procedures或者receding horizon procedure 或者Model predictive control。但是这里的问题是，如果我们希望能够求解出最优解，那么H一般就需要非常非常短，因此可以求助于approximation的策略，可以分为确定性策略和随机性策略。

Deterministic forecasts
将未来的随机变量表示成确定性的数值，然后将t到t+H时间段内的问题表述成一个优化问题，通过解这个优化问题，得到当前的最优动作。然后采取动作，进入下一个确定性的状态，再重复上面的步骤。
这种确定性模型的好处是可以求解动作是连续的情况，而且可以应对问题的不稳定性。
但是，确定性模型难以解决未来情况的不确定性。

Stochastic forecasts
一种将上面deterministic rolling horizon procedure策略改进到可以解决未来不确定性的方法是通过stochistic programming, 但是这种多阶段的随机规划往往计算复杂度会非常高，一种解决策略是引入一些近似。
比如将问题分解为两个阶段。第一阶段是在t时，假设知道St，然后进行决策xt；第二阶段是在t+1时，我们假设我们知道从t+1到t+H的所有信息，即可以认为xt+1可以看到未来所有信息。
但是上面这种假设仍然不能让我们解决随机问题。因此可以采用蒙特卡罗采样的方法：即根据概率随机采样出一批轨迹，然后对于每一条轨迹类似于确定性策略进行优化，并且加上 nonanticipativity 的约束，让xtt(w)是一致的，来符合前面的假设。

这种方法的优点是能够捕捉到未来的不确定性，缺点是因为对多条采样轨迹进行优化，相当于重复了多次确定性优化，会大大增加计算量。

Rolling horizon with discounting
动态规划中很重要的一种目标函数形式：

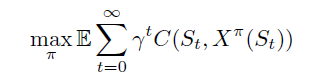
discounting的出发点是因为，对于t时刻做出的决策，时间越远的奖励，其实影响越小，因此对于rolling horizon policy，一般可以进行如下修正：

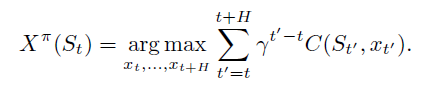
三、Policy Function Approximations(策略函数估计）

前面的lookahead策略，尽管进行了一些近似，但是仍然是computationally demanding的，因此许多学者希望去探寻一种更加快速的策略。
本节的内容就是聚焦于找到一个直接从状态返回动作的函数。

1.Lookup table policies

适用于状态和动作都是离散的情况。
对于每一个状态，以及此状态下可能采取的每一个动作，都对应着一个价值函数。
这是一种不够紧凑的表达形式，虽然lookuo tables很容易被理解，但实际上很难进行优化。

2.Parametric policy models

Designing parametric policy function approximations is an art form.
我们的目标就是找到下式策略函数中的θ：

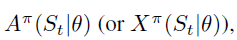
然后怎么找到最优的θ呢？通过求解如下的优化问题：

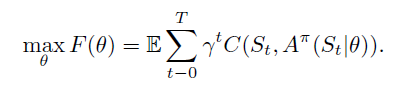
另一种方法如下：

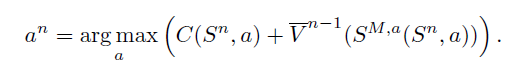
就是通过拟合价值函数，然后直接得到策略函数的参数。（但是这里不就得陷入如何拟合价值函数的循环？？？）

3.Nonparametric policy models

比如用神经网络来近似策略函数。而不是使用具体的参数。（类似于强化学习的方法？？？）

四、Value Function Approximations（价值函数估计）

价值函数估计的方法就是通过一些近似的形式来拟合状态价值函数。即根据如下式子进行决策：

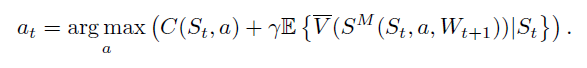
1.Lookup tables

如果state是离散的，就可以用一张表存储每个状态的价值。通过如下公式来更新状态价值：

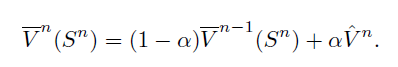
2.Parametric models

利用解析函数来表示状态的价值，其中函数中包含参数θ，参数的维度要远远比state的维度低。
lookup table往往面临维度爆炸的问题，因此可以用回归模型来进行近似。
首先我们可以从状态中提取特征：

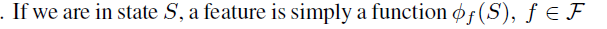
然后将特征映射到状态价值函数：

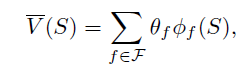
但是怎么设计这个参数是一项艺术工作。
但是问题是，我们可能不容易找到正确的basis functions。

3.Nonparametric models

比如神经网络函数，可以不用设计精巧的解析函数。通过观测去估计出每个状态的价值函数，比如：

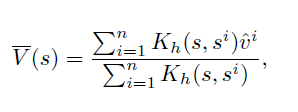
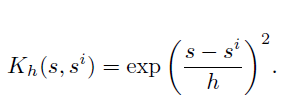
参数模型会给定一个函数的形式，但是非参数模型不会固定函数形式，因此具有更大的灵活性。

五、Hybrid Strategies（混合策略）

myopic policies, lookahead policies, policies based on value function approximations, and policy function approximation代表了近似解决动态规划问题的核心工具。然而这些方法也是可以进行混合的。
Myopic policies with tunable parameters
在贪婪策略中加入一些参数，比如根据时间紧迫反映奖励的参数。

Rolling horizon procedures with value function approximations
将仿真一定步长状态价值函数近似进行结合，如下：

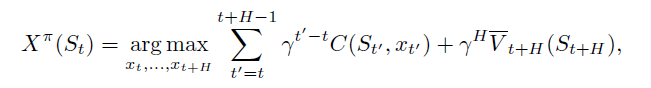
Rolling horizon procedures with tunable policies
因为rolling策略中的确定性策略往往不会考虑到未来的不确定性，因此可以加入一些可以调节参数的策略，来增加向前仿真过程中，可能的冗余度。

Rollout heuristics with policy function approximation
在Rollout策略中，需要向前进行仿真，其中一半选择myopic策略作为向前仿真的策略，但是也可以和策略函数近似方法进行结合。

Tree search with rollout heuristic and a lookup table policy
先进行很短几步的tree search，然后再进行rollout策略

Value function approximation with lookup table or policy function approximation

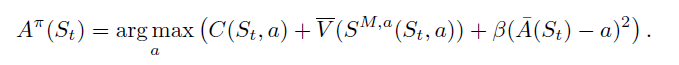
六、Randomized Policies（随机策略）

考虑exploration和exploitation。比如e-greedy策略。greedy in the limit with infinite exploration
或者Boltzmann exploration（也叫作Gibbs sampling, soft-max policy）

总结

提示：这里对文章进行总结：
那么我们应该怎么选择一个合适的策略呢？
1、myopic 策略能够解决问题吗？如果不能，那可以作为一个好的开头吗？
2、这个问题稳定吗？如果问题和时间相关，比如时变需求，那么需要和时间相关策略，比如rolling 策略，这种情况下一般策略函数近似可能效果不好。
3、如果考虑近似表示状态价值，那么状态价值可以表示为一个很简单的问题吗？如果很复杂，那么很难用参数函数取近似，

最后

以上就是典雅仙人掌为你收集整理的Approximate Dynamic Programming（近似动态规划算法） Chapter 6 阅读笔记前言一、Myopic Policies（贪婪策略）二、Lookahead Policies(前视策略）三、Policy Function Approximations(策略函数估计）四、Value Function Approximations（价值函数估计）五、Hybrid Strategies（混合策略）六、Randomized Policies（随机策略）总结的全部内容，希望文章能够帮你解决Approximate Dynamic Programming（近似动态规划算法） Chapter 6 阅读笔记前言一、Myopic Policies（贪婪策略）二、Lookahead Policies(前视策略）三、Policy Function Approximations(策略函数估计）四、Value Function Approximations（价值函数估计）五、Hybrid Strategies（混合策略）六、Randomized Policies（随机策略）总结所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。