Bandit算法是在线学习的一种,一切通过数据收集而得到的概率预估任务,都能通过Bandit系列算法来进行在线优化。这里的“在线”,指的不是互联网意义上的线上,而是只算法模型参数根据观察数据不断演变。
以多臂老虎机问题为例,首先我们假设每个臂是否产生收益,其背后有一个概率分布,产生收益的概率为p
我们不断地试验,去估计出一个置信度较高的概率p的概率分布就能近似解决这个问题了。
怎么能估计概率p的概率分布呢? 答案是假设概率p的概率分布符合beta(wins, lose)分布,它有两个参数: wins, lose。
每个臂都维护一个beta分布的参数。每次试验后,选中一个臂,摇一下,有收益则该臂的wins增加1,否则该臂的lose增加1。
初始化beta参数 胜率和败率都为0.5
prior_a = 1. # aka successes
prior_b = 1. # aka failures
estimated_beta_params = np.zeros((K,2))
estimated_beta_params[:,0] += prior_a # allocating the initial conditions
estimated_beta_params[:,1] += prior_b
beta参数要在后面的计算中不断更新的。
-------------------------------------------------------------------------------------------
Beta分布:
对于硬币或者骰子这样的简单实验,我们事先能很准确地掌握系统成功的概率。然而通常情况下,系统成功的概率是未知的。为了测试系统的成功概率p,我们做n次试验,统计成功的次数k,于是很直观地就可以计算出p=k/n。然而由于系统成功的概率是未知的,这个公式计算出的p只是系统成功概率的最佳估计。也就是说实际上p也可能为其它的值,只是为其它的值的概率较小。
例如有某种特殊的硬币,我们事先完全无法确定它出现正面的概率。然后抛10次硬币,出现5次正面,于是我们认为硬币出现正面的概率最可能是0.5。但是即使硬币出现正面的概率为0.4,也会出现抛10次出现5次正面的情况。因此我们并不能完全确定硬币出现正面的概率就是0.5,所以p也是一个随机变量,它符合Beta分布。
Beta分布是一个连续分布,由于它描述概率p的分布,因此其取值范围为0到1。
Beta分布有α和β两个参数,其中α为成功次数加1,β为失败次数加1。
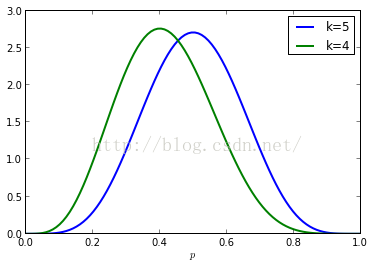
连续分布用概率密度函数描述,下面绘制实验10次,成功4次和5次时,系统成功概率p的分布情况。可以看出k=5时,曲线的峰值在p=0.5处,而k=4时,曲线的峰值在p=0.4处。
n = 10
k = 5
p = np.linspace(0, 1, 100)
pbeta = stats.beta.pdf(p, k+1, n-k+1)
plot(p, pbeta, label="k=5", lw=2)
k = 4
pbeta = stats.beta.pdf(p, k+1, n-k+1)
plot(p, pbeta, label="k=4", lw=2)
xlabel("$p$")
legend(loc="best");
 ----------------------------------------------------------------------------------------------------------------
----------------------------------------------------------------------------------------------------------------
几个bandit算法:
我们先从最简单的开始,先试几次,每个臂都有了均值之后,一直选均值最大那个臂。这个算法是我们人类在实际中最常采用的,不可否认,它还是比随机乱猜要好。
def naive(estimated_beta_params,number_to_explore=100):
totals = estimated_beta_params.sum(1) # totals
if np.any(totals < number_to_explore): # if have been explored less than specified
least_explored = np.argmin(totals) # return the one least explored
return least_explored
else: # return the best mean forever
successes = estimated_beta_params[:,0] # successes
estimated_means = successes/totals # the current means
best_mean = np.argmax(estimated_means) # the best mean
return best_mean
下一个,Thompson sampling算法:
简单介绍一下它的原理:
每次选择臂的方式是:用每个臂现有的beta分布产生一个随机数b,选择所有臂产生的随机数中最大的那个臂去摇。
以上就是Thompson采样,用python实现就一行:
np.argmax(pymc.rbeta(1 + successes, 1 + totals - successes))
第三个是UCB算法:
UCB算法全称是Upper Confidence Bound(置信区间上界),算法的具体步骤如下:
先对每一个臂都试一遍
之后,每次选择以下值最大的那个臂
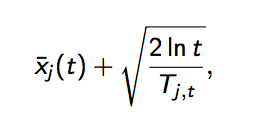
其中加号前面是这个臂到目前的收益均值,后面的叫做bonus,本质上是均值的标准差,置信区间可以简单地理解为不确定性的程度,区间越宽,越不确定,反之亦反之。t是目前的试验次数,Tjt是这个臂被试次数。
这个公式反映:均值越大,标准差越小,被选中的概率会越来越大,起到了exploit的作用;同时哪些被选次数较少的臂也会得到试验机会,起到了explore的作用。
每个item的回报均值都有个置信区间,随着试验次数增加,置信区间会变窄(逐渐确定了到底回报丰厚还是可怜)。
每次选择前,都根据已经试验的结果重新估计每个item的均值及置信区间。
选择置信区间上限最大的那个item。
“选择置信区间上界最大的那个item”这句话反映了几个意思:
- 如果item置信区间很宽(被选次数很少,还不确定),那么它会倾向于被多次选择,这个是算法冒风险的部分;
- 如果item置信区间很窄(备选次数很多,比较确定其好坏了),那么均值大的倾向于被多次选择,这个是算法保守稳妥的部分;
- UCB是一种乐观的算法,选择置信区间上界排序,如果时悲观保守的做法,是选择置信区间下界排序。
def UCB(estimated_beta_params):
t = float(estimated_beta_params.sum()) # total number of rounds
totals = estimated_beta_params.sum(1) #The number of experiments per arm
successes = estimated_beta_params[:,0]
estimated_means = successes/totals # earnings mean
estimated_variances = estimated_means - estimated_means**2
UCB = estimated_means + np.sqrt( np.minimum( estimated_variances + np.sqrt(2*np.log(t)/totals), 0.25 ) * np.log(t)/totals )
return np.argmax(UCB)
第四个,Epsilon-Greedy算法:
选一个(0,1)之间较小的数epsilon
每次以概率epsilon(产生一个[0,1]之间的随机数,比epsilon小)做一件事:所有臂中随机选一个。否则,选择截止当前,平均收益最大的那个臂。
是不是简单粗暴?epsilon的值可以控制对Exploit和Explore的偏好程度。越接近0,越保守,只想花钱不想挣钱。
代码:
from arm import Arm
import random
import numpy as np
def mean(values):
return sum(values)*1.0/len(values)
class EpsilonGreedyAlgorithm(object):
def __init__(self, arms, epsilon):
self.epsilon = epsilon
self.arms = arms
self.values = [[] for i in arms]
def select_arm(self):
if random.random() > self.epsilon:
arm_idx = self.get_best_arm_idx()
else:
arm_idx = self.get_random_arm_idx()
arm = self.arms[arm_idx]
reward = arm.pull()
self.update(arm_idx, reward)
def update(self, arm_idx, reward):
self.values[arm_idx].append(reward)
def get_best_arm_idx(self):
max_yhat = 0.0
max_idx = None
for i, values in enumerate(self.values):
yhat = 0.0 if len(values) == 0 else mean(values)
if yhat > max_yhat:
max_yhat = yhat
max_idx = i
if max_idx is None:
return self.get_random_arm_idx()
else:
return max_idx
def get_random_arm_idx(self):
return random.randrange(len(self.arms))
if __name__=="__main__":
epsilon = 0.1
ps = [random.random() for i in range(random.randrange(2, 8))]
arms = [Arm(p) for p in ps]
algo = EpsilonGreedyAlgorithm(arms, epsilon=epsilon)
for i in range(100):
algo.select_arm()
total_reward = 0
for i, vals in enumerate(algo.values):
total_reward += sum(vals)
print "reward:", total_reward, "t epsilon:", epsilon
Bandit算法是在线学习的一种,一切通过数据收集而得到的概率预估任务,都能通过Bandit系列算法来进行在线优化。这里的“在线”,指的不是互联网意义上的线上,而是只算法模型参数根据观察数据不断演变。
以多臂老虎机问题为例,首先我们假设每个臂是否产生收益,其背后有一个概率分布,产生收益的概率为p
我们不断地试验,去估计出一个置信度较高的概率p的概率分布就能近似解决这个问题了。
怎么能估计概率p的概率分布呢? 答案是假设概率p的概率分布符合beta(wins, lose)分布,它有两个参数: wins, lose。
每个臂都维护一个beta分布的参数。每次试验后,选中一个臂,摇一下,有收益则该臂的wins增加1,否则该臂的lose增加1。
初始化beta参数 胜率和败率都为0.5 prior_a = 1. # aka successes
prior_b = 1. # aka failures
estimated_beta_params = np.zeros((K,2))
estimated_beta_params[:,0] += prior_a # allocating the initial conditions
estimated_beta_params[:,1] += prior_b-------------------------------------------------------------------------------------------
Beta分布:
对于硬币或者骰子这样的简单实验,我们事先能很准确地掌握系统成功的概率。然而通常情况下,系统成功的概率是未知的。为了测试系统的成功概率p,我们做n次试验,统计成功的次数k,于是很直观地就可以计算出p=k/n。然而由于系统成功的概率是未知的,这个公式计算出的p只是系统成功概率的最佳估计。也就是说实际上p也可能为其它的值,只是为其它的值的概率较小。
例如有某种特殊的硬币,我们事先完全无法确定它出现正面的概率。然后抛10次硬币,出现5次正面,于是我们认为硬币出现正面的概率最可能是0.5。但是即使硬币出现正面的概率为0.4,也会出现抛10次出现5次正面的情况。因此我们并不能完全确定硬币出现正面的概率就是0.5,所以p也是一个随机变量,它符合Beta分布。
Beta分布是一个连续分布,由于它描述概率p的分布,因此其取值范围为0到1。
Beta分布有α和β两个参数,其中α为成功次数加1,β为失败次数加1。
连续分布用概率密度函数描述,下面绘制实验10次,成功4次和5次时,系统成功概率p的分布情况。可以看出k=5时,曲线的峰值在p=0.5处,而k=4时,曲线的峰值在p=0.4处。
n = 10
k = 5
p = np.linspace(0, 1, 100)
pbeta = stats.beta.pdf(p, k+1, n-k+1)
plot(p, pbeta, label="k=5", lw=2)
k = 4
pbeta = stats.beta.pdf(p, k+1, n-k+1)
plot(p, pbeta, label="k=4", lw=2)
xlabel("$p$")
legend(loc="best");
几个bandit算法:
我们先从最简单的开始,先试几次,每个臂都有了均值之后,一直选均值最大那个臂。这个算法是我们人类在实际中最常采用的,不可否认,它还是比随机乱猜要好。
def naive(estimated_beta_params,number_to_explore=100):
totals = estimated_beta_params.sum(1) # totals
if np.any(totals < number_to_explore): # if have been explored less than specified
least_explored = np.argmin(totals) # return the one least explored
return least_explored
else: # return the best mean forever
successes = estimated_beta_params[:,0] # successes
estimated_means = successes/totals # the current means
best_mean = np.argmax(estimated_means) # the best mean
return best_mean下一个,Thompson sampling算法:
简单介绍一下它的原理:
每次选择臂的方式是:用每个臂现有的beta分布产生一个随机数b,选择所有臂产生的随机数中最大的那个臂去摇。
以上就是Thompson采样,用python实现就一行:
np.argmax(pymc.rbeta(1 + successes, 1 + totals - successes))
第三个是UCB算法:
UCB算法全称是Upper Confidence Bound(置信区间上界),算法的具体步骤如下:
先对每一个臂都试一遍
之后,每次选择以下值最大的那个臂
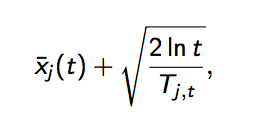
其中加号前面是这个臂到目前的收益均值,后面的叫做bonus,本质上是均值的标准差,置信区间可以简单地理解为不确定性的程度,区间越宽,越不确定,反之亦反之。t是目前的试验次数,Tjt是这个臂被试次数。
这个公式反映:均值越大,标准差越小,被选中的概率会越来越大,起到了exploit的作用;同时哪些被选次数较少的臂也会得到试验机会,起到了explore的作用。
每个item的回报均值都有个置信区间,随着试验次数增加,置信区间会变窄(逐渐确定了到底回报丰厚还是可怜)。
每次选择前,都根据已经试验的结果重新估计每个item的均值及置信区间。
选择置信区间上限最大的那个item。
“选择置信区间上界最大的那个item”这句话反映了几个意思:
- 如果item置信区间很宽(被选次数很少,还不确定),那么它会倾向于被多次选择,这个是算法冒风险的部分;
- 如果item置信区间很窄(备选次数很多,比较确定其好坏了),那么均值大的倾向于被多次选择,这个是算法保守稳妥的部分;
- UCB是一种乐观的算法,选择置信区间上界排序,如果时悲观保守的做法,是选择置信区间下界排序。
第四个,Epsilon-Greedy算法:def UCB(estimated_beta_params): t = float(estimated_beta_params.sum()) # total number of rounds totals = estimated_beta_params.sum(1) #The number of experiments per arm successes = estimated_beta_params[:,0] estimated_means = successes/totals # earnings mean estimated_variances = estimated_means - estimated_means**2 UCB = estimated_means + np.sqrt( np.minimum( estimated_variances + np.sqrt(2*np.log(t)/totals), 0.25 ) * np.log(t)/totals ) return np.argmax(UCB)
选一个(0,1)之间较小的数epsilon
每次以概率epsilon(产生一个[0,1]之间的随机数,比epsilon小)做一件事:所有臂中随机选一个。否则,选择截止当前,平均收益最大的那个臂。
是不是简单粗暴?epsilon的值可以控制对Exploit和Explore的偏好程度。越接近0,越保守,只想花钱不想挣钱。
代码:
from arm import Arm import random import numpy as np def mean(values): return sum(values)*1.0/len(values) class EpsilonGreedyAlgorithm(object): def __init__(self, arms, epsilon): self.epsilon = epsilon self.arms = arms self.values = [[] for i in arms] def select_arm(self): if random.random() > self.epsilon: arm_idx = self.get_best_arm_idx() else: arm_idx = self.get_random_arm_idx() arm = self.arms[arm_idx] reward = arm.pull() self.update(arm_idx, reward) def update(self, arm_idx, reward): self.values[arm_idx].append(reward) def get_best_arm_idx(self): max_yhat = 0.0 max_idx = None for i, values in enumerate(self.values): yhat = 0.0 if len(values) == 0 else mean(values) if yhat > max_yhat: max_yhat = yhat max_idx = i if max_idx is None: return self.get_random_arm_idx() else: return max_idx def get_random_arm_idx(self): return random.randrange(len(self.arms)) if __name__=="__main__": epsilon = 0.1 ps = [random.random() for i in range(random.randrange(2, 8))] arms = [Arm(p) for p in ps] algo = EpsilonGreedyAlgorithm(arms, epsilon=epsilon) for i in range(100): algo.select_arm() total_reward = 0 for i, vals in enumerate(algo.values): total_reward += sum(vals) print "reward:", total_reward, "t epsilon:", epsilon
最后
以上就是害羞牛排最近收集整理的关于bandit算法原理及Python实现的全部内容,更多相关bandit算法原理及Python实现内容请搜索靠谱客的其他文章。








发表评论 取消回复