一、Critic的作用
Critic就是一个神经网络,以状态 s s s 为输入,以期望的Reward为输出。
- Critic的作用就是衡量一个Actor在某State状态下的优劣。Given an actor π, it evaluates the how good the actor is。
- Critic本身不能决定要采取哪一个Action。A critic does not determine the action.
- An actor can be found from a critic.
- Critic是依赖于Actor的,因为不同迭代周期的Actor π π π是不同的,所以即使输入相同的State,Critic输出的Reward也是不同的。
- Critic输出的Reward的大小取决于两个因素:
- 所处的State;
- 所要评价的Actor;
- Actor和Critic的区别:Actor是以 s s s 为输入,输出对应的 action 和其概率;Criti则是以 s s s 为输入,输出对应的reward期望值。
- 如何获得Critic:直接使用一个神经网络,以状态s为输入,value为输出即可。
- Policy-Based Approach 中,我们定义如下梯度用来更新
θ
θ
θ
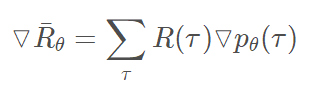
- 这其中 R ( τ ) R(τ) R(τ) 是machine与环境互动所获得的实际reward,这就导致具有很大的不确定性。因为machine采取什么样的动作是一种概率性的行为,而同一个动作,环境给予什么样的reward也是具有随机性的,这样将会导致machine的学习效率比较低下,就像没头苍蝇乱撞,可能学习很久都找不到正确的方向。所以我们要给machine一个正确的方向,即使用它的期望值代替实际的reward,期望值是可以被估算、计算的,这样就有利于我们去设计特定的函数来估算、计算期望的reward,从而引导我们的machine去做出我们想要的action。
二、Critic种类
Critic有很多种,比如:State value function V π ( s ) V^π(s) Vπ(s)、State-Action value function Q π ( s , a ) Q^π(s,a) Qπ(s,a)
1、State value function V π ( s ) V^π(s) Vπ(s):只考虑state s s s
V
π
(
s
)
V^π(s)
Vπ(s) 表示:在使用 Actor
π
π
π 的情况下,从观察到状态
s
s
s 的时刻
t
t
t 直到该轮episode结束所能得到的 累计 Reward 。When using actor
π
π
π, the cumulated reward expects to be obtained after seeing observation (state)
s
t
s_t
st until the end of this episode。
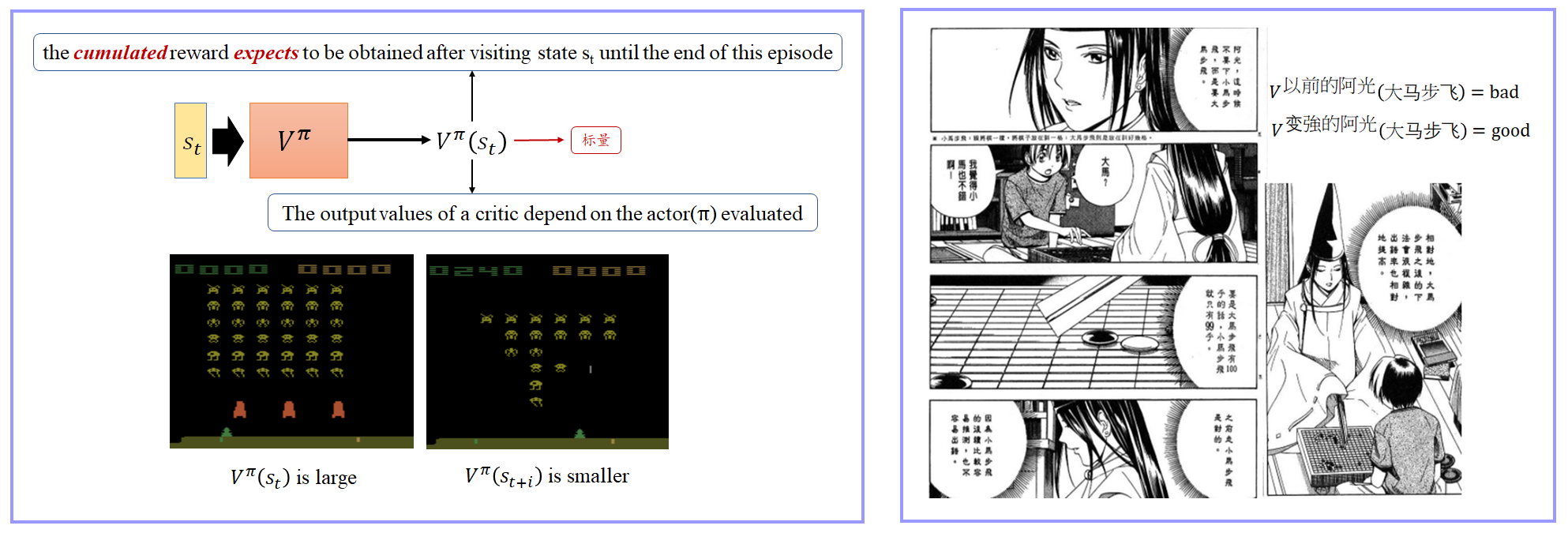
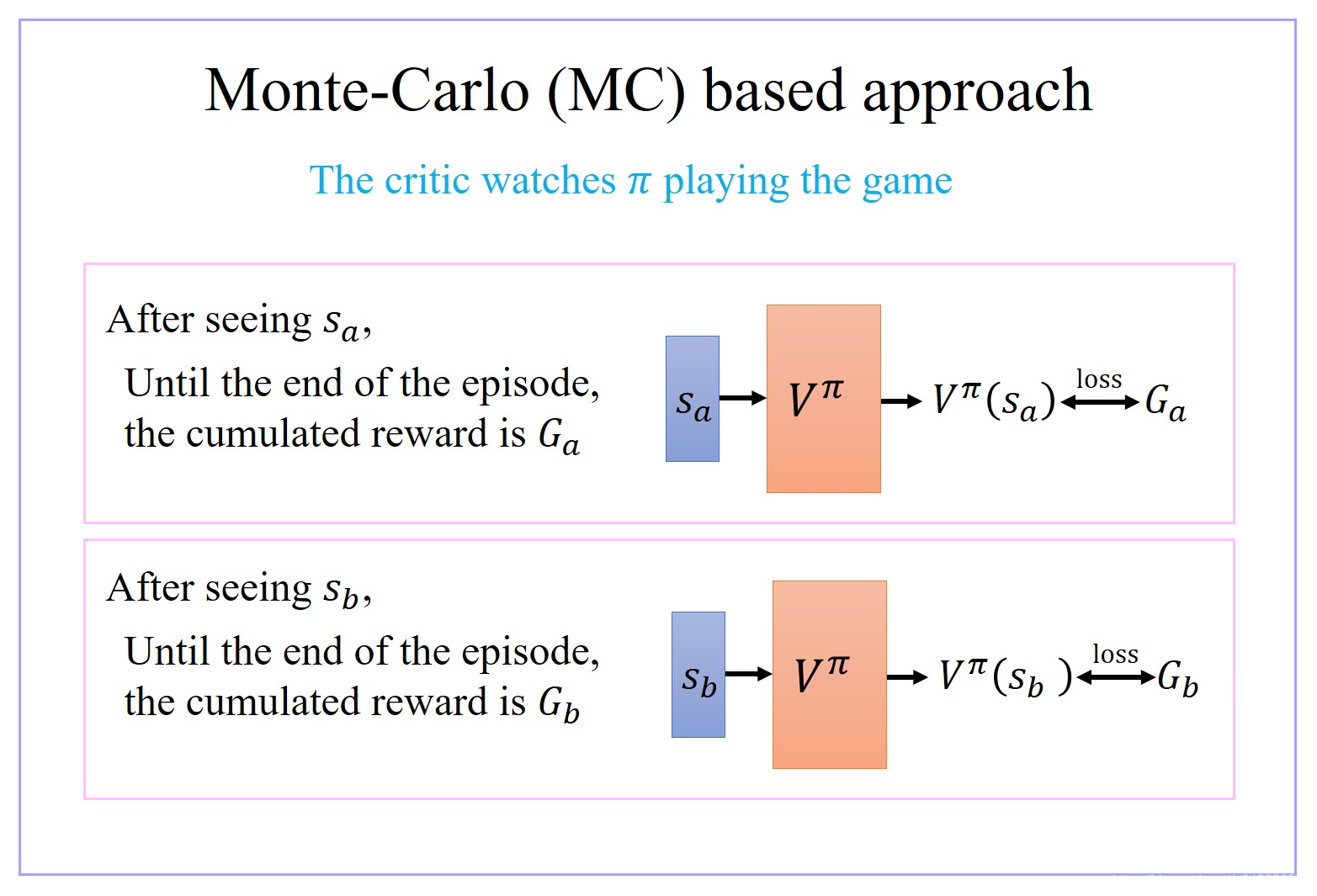
1.1 V π ( s ) V^π(s) Vπ(s) 评价方法01:Monte-Carlo(MC) based approach
- Critic 就去看那个 actor π π π 玩游戏,看 actor π π π 玩得怎么样
- 假设现在 Critic 观察到 actor π π π 经过 state S a S_a Sa 以后直到这轮游戏结束,它会得到的 accumulated 的 reward G a G_a Ga,就要说如果 Critic 的 input 为 state S a S_a Sa,那 Critic 的 output 要跟 G a G_a Ga 越接近越好。这不过是一个 regression 的问题。这个 actor 要调它的参数,那它的 output 跟 G a G_a Ga 越接近越好
- 假设现在 Critic 观察到 actor π π π 经过 state S b S_b Sb 以后直到这轮游戏结束,它会得到的 accumulated 的 reward G b G_b Gb,就要说如果 Critic 的 input 为 state S b S_b Sb,那 Critic 的 output 要跟 G b G_b Gb 越接近越好。这不过是一个 regression 的问题。这个 actor 要调它的参数,那它的 output 跟 G b G_b Gb 越接近越好
1.2 V π ( s ) V^π(s) Vπ(s) 的优劣方法02:Temporal-difference(TD) approach
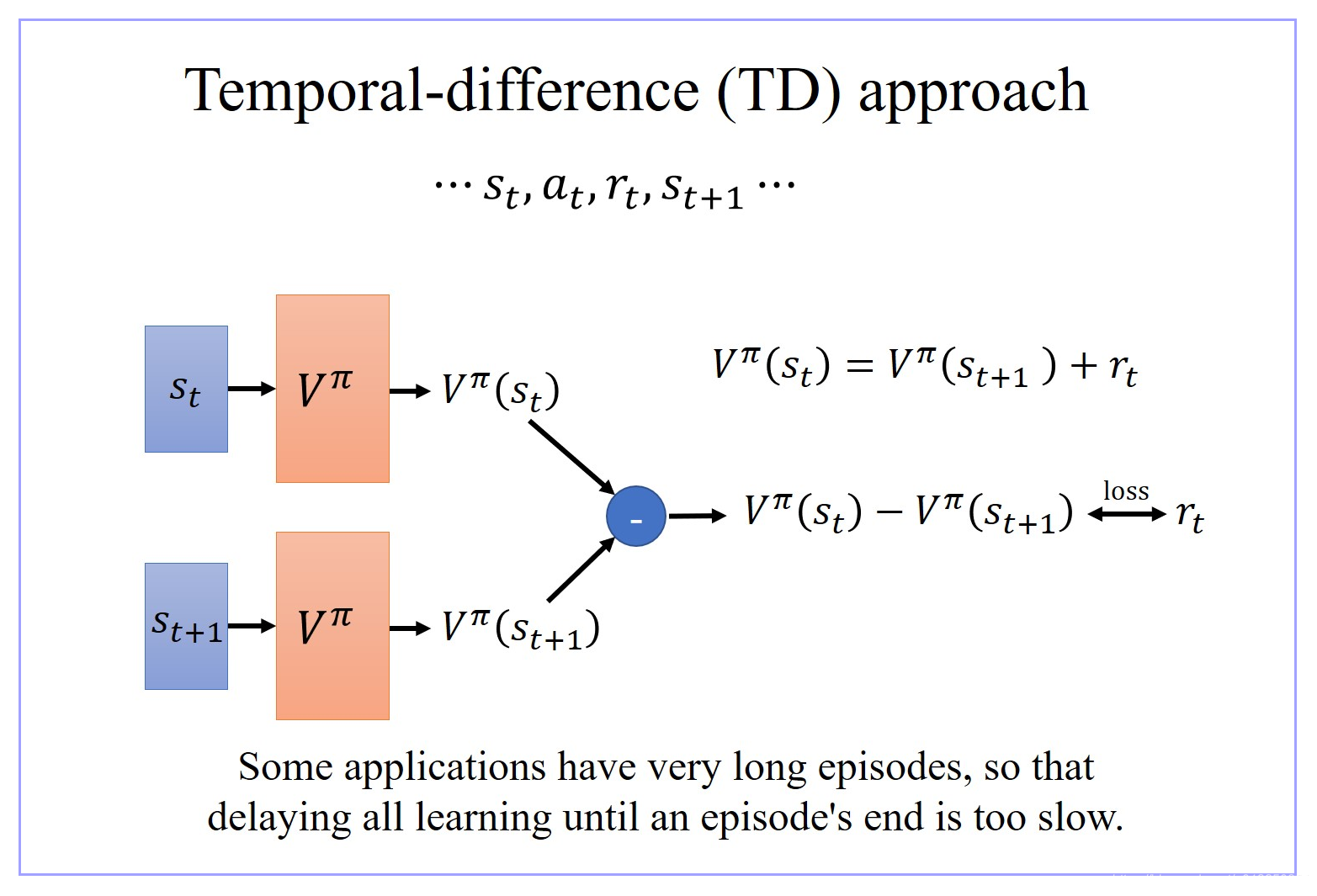
- 有时候有些游戏非常的长,如果你没有办法一边玩游戏,一边 update 你的 network 的话,那你会搞太久。
- 用 Temporal-difference(TD) 方法,有一个非常明确的好处,就是当游戏还没有结束,玩到一半的时候,就可以开始 update 你的 network
1.3 MC v.s. TD
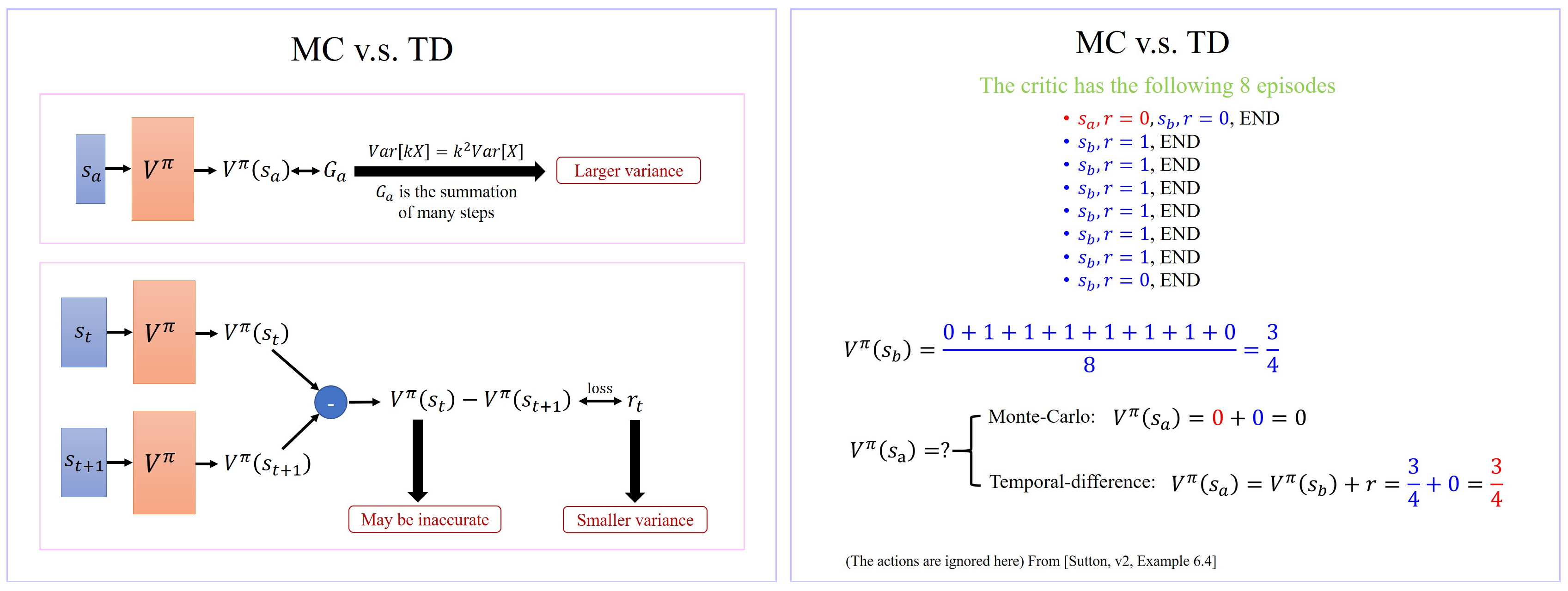
- Monte-Carlo(MC) based approach 的优势是比用TD方法精确,但是最大的问题就是它的 Various 很大。因为 G a G_a Ga 其实是很多个不同的 step 的 reward 的和,假设每一个 step 都会得到一个 reward, G a G_a Ga 是从 state s a s_a sa 开始,一直玩到游戏结束,每一个 s i s_i si 的reward 的和 Reward G a G_a Ga 的 Variance 相较于某一个 state s i s_i si 的 reward 会是比较大的。
- Temporal-difference(TD) approach 方法中会有随机性的是 r t r_t rt,因为你在 s t s_t st 状态下就算你采取同一个 action,得到的 reward 也不见得是一样的。所以 r t r_t rt 其实也是一个 random variable。但这个 random variable 它的 variance 会比 MC 方法中的 G a G_a Ga 还要小,因为 MC 方法中的 G a G_a Ga 是很多个不同的 step 的 reward 的和,而 TD 的 r t r_t rt 只是某一个 step 的 reward 而已,TD 中的 r t r_t rt 的 variance 会比MC方法中的 G a G_a Ga 的 variance 小。
- TD 方法相比较MC方法出现的新问题是: V π ( s t ) V^π(s_t) Vπ(st) 不一定估的准确。如果 V π ( s t ) V^π(s_t) Vπ(st) 估的是不准的,那你 apply 这个式子 learn 出来的结果,其实也会是不准的。
- MC 跟 TD 它们是各有优劣。可以有一个MC 跟 TD 综合的版本,balance between MC and TD:Multi-step Experience Reply Buffer。
- 实践中,MC 跟TD 估出来的结果很有可能是不一样的。就算 Critic 观测到一样的 training data,MC 跟TD 最后估出来的结果,也不见得会是一样。
- MC 跟 TD是不同的方法,它考虑了不同的假设,最后会得到不同的运算结果。
- 实践中,其实 Temporal-difference(TD) approach 的方法是比较常用的,Monte-Carlo(MC) based approach 的方法其实是比较少用的。
2、State-Action value function Q π ( s , a ) Q^π(s,a) Qπ(s,a):同时考虑state s s s、action a a a
在使用 Actor
π
π
π 的情况下,观察到状态
s
i
s_i
si 下强制采取某一个策略/action
a
a
a ( Actor
π
π
π 在状态
s
i
s_i
si 下备选的策略/action不一定只有
a
a
a,可能还有
b
,
c
,
d
.
.
.
b,c,d...
b,c,d...) ,从观察到状态
s
i
s_i
si的时刻直到该轮episode结束所能得到的累计Reward。When using actor
π
π
π, the cumulated reward expects to be obtained after seeing observation
s
s
s and taking action
a
a
a until the end of this episode。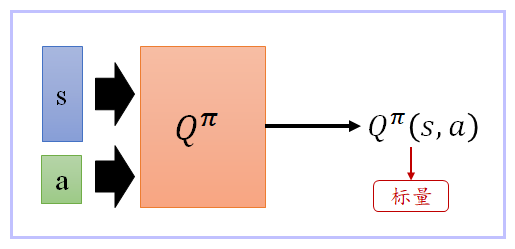
- Q π ( s , a ) Q^π(s,a) Qπ(s,a) 理论上它会有两个 input, s s s 跟 a a a, Q π ( s , a ) Q^π(s,a) Qπ(s,a) 吃 s s s 跟 a a a 来决定说它要得到多少的分数
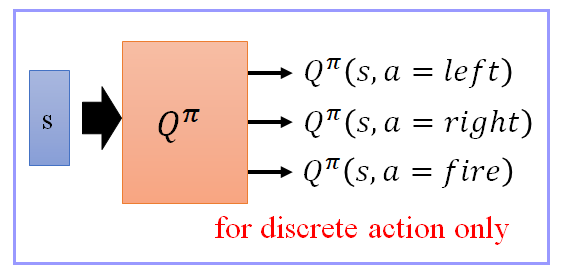
- 有时候我们会改写这个 Q function,假设你的 a a a 策略/action 是可以穷举的,举例来说,在玩游戏的时候, a a a 只有向左/向右,跟开火三个选择
- 我们的 Q function 是 input 一个 state s,它的 output 分别就是 Q π ( s , a = l e f t ) Q^π(s, a=left) Qπ(s,a=left), Q π ( s , a = r i g h t ) Q^π(s, a=right) Qπ(s,a=right), Q π ( s , a = f i r e ) Q^π(s, a=fire) Qπ(s,a=fire)
- 这样的好处就是,你只要输入一个 state s ,你就可以知道,s 配上,向左的时候,分数是多少,s 配上向右的时候,分数是多少,s 配上开火的时候,分数是多少。
三、Q-Learning:从 Q π ( s , a ) Q^π(s,a) Qπ(s,a) 中训练得到 Actor/Policy π π π
1、Policy Gradient 和 Q-Learning 的区别
- Q-learning通过将 ( a t , s t ) (a_t,s_t) (at,st)输入Q function来求得对应的Q值:Q ( a t , s t ) (a_t,s_t) (at,st),然后选择对应Q值最大的那个action。这个Q function可以是一张表,查阅Q表中相应的 ( a t , s t ) (a_t,s_t) (at,st)即可得到相应的Q值;但是实际环境中 ( a t , s t ) (a_t,s_t) (at,st)太多了,构造出所有组合的Q表不太现实。所以DQN使用一个神经网络来逼近Q function,从而达到输入一组 ( a t , s t ) (a_t,s_t) (at,st)就可以得到相应Q值的目的。
- Q-learning中的agent如何去选择用哪一个action呢?在某一个state下,它求出有限action集合中所有action所对应的Q值,然后选择所对应Q值最大的那个action作为目标action。(具体实现时使用 ϵ−greed 策略而不是简单选取最大Q值)
- 而policy gradient如何选择action呢?它将state 输入一个policy 网络,直接预测目标action。这个policy网络通过long term reward的梯度反向传播,来更新policy网络的权重。这个long term reward就是一个关于reward的函数,表达一段时间内预期得到的奖励。
- 综上,Q-learning通过 ( a t , s t ) (a_t,s_t) (at,st) 来计算Q值,再反过来选取对应最大Q值的那一个action作为目标action;而 policy gradient则是直接根据st来计算最优的action。即:Q-learning中网络输出的是Q值,policy-gradient中网络输出的值是action。它们的区别就像生成类模型和判别类模型的区别(生成类模型先计算联合分布然后做出分类,而判别类模型直接根据后验分布进行分类)。
- Q-learning的缺点:由于Q-learning的做法是“选取一个使Q最大的action”: π ′ ( s ) = arg max a Q π ( s , a ) π'(s)=argmax_aQ^π(s,a) π′(s)=argmaxaQπ(s,a),因此这个action的取值空间通常是有限且离散的,Q-learning不太容易处理连续的 action,因为无法穷举所有可能的连续action(比如:自驾车的方向盘转的角度、机器人关节的扭转角度等);而policy gradient则不存在这个问题,因为它通过policy模型根据state直接输出最优的action,那么这个action可以是任意连续的值。面对一个很大的action集合,Q-learning要计算很多遍Q值,即进行很多遍神经网络的前馈过程;相比之下,policy gradient的网络只需进行一遍网络的前馈,输出一个action值,然后与action集合中的各个值比较,选取最接近的那一个action即可。
- Q-learning 跟 Policy-Gradient 方法比起来更稳,Policy-Gradient 方法其实是没有太多游戏可以玩得起来的。所以 policy gradient 其实比较不稳,尤其在没有 PPO(Proximal Policy Optimization)之前很难用 policy gradient 做什么事情。
2、Critic和Q-Learning的区别
- Critic是只计算期望的reward,并不会根据这个reward选择action;
- 而 Q-Learning 则会根据估算出来的reward选择最大的那个reward对应的action。Used in Value-based Approach to learn an Actor/Policy π
3、Q-Learning更新Actor/Policy的过程
- 虽然表面上我们 learn 一个 Q function Q π ( s , a ) Q^π(s,a) Qπ(s,a) 只能拿来评估某一个 actor π π π的好坏,但是实际上只要有了这个 Q π ( s , a ) Q^π(s,a) Qπ(s,a),我们就可以做 reinforcement learning。
- 其实有这个 Q π ( s , a ) Q^π(s,a) Qπ(s,a) ,我们就可以决定要采取哪一个 action。
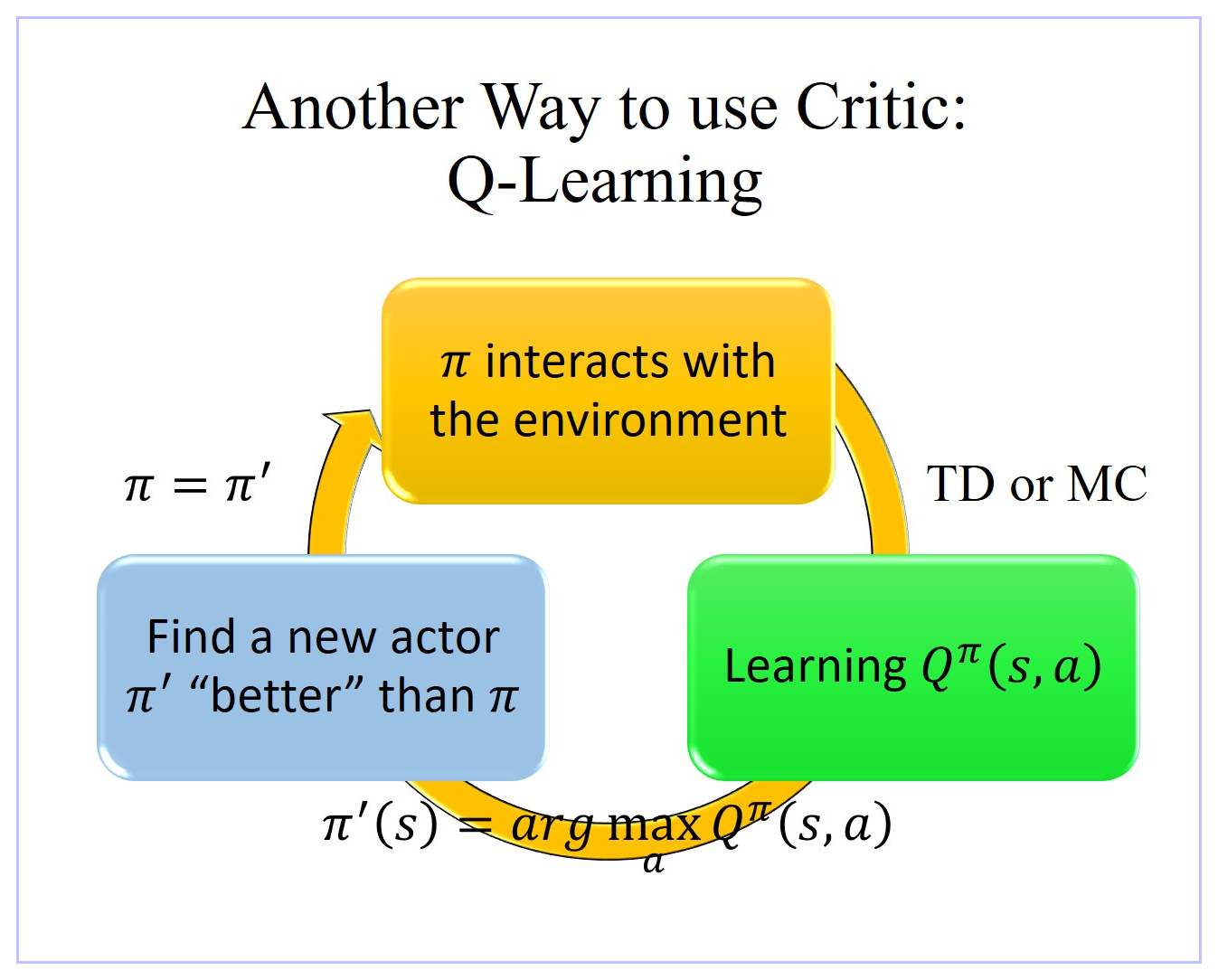
- 大致过程:假设你有一个初始的 actor π π π,也许一开始很烂,随机的也没有关系,用这个 actor π π π 跟环境互动取样,接下来根据采样数据 learn 出 π π π 这个 actor 的 Q π ( s , a ) Q^π(s,a) Qπ(s,a) 值, Q π ( s , a ) Q^π(s,a) Qπ(s,a) 值是衡量 π π π 这个 actor 在某一个 state 强制采取某一个 action 会得到的 expected reward,可以用 TD方法也可以用 MC方法。
- 只要 π π π 根据采样数据 learn 得出一个 Q π ( s , a ) Q^π(s,a) Qπ(s,a) ,就保证可以找到一个新的 π ′ π' π′一定会比原来的 π π π 更好。用 π ′ π' π′ 将 π π π 取代掉,然后继续找 π ′ π' π′ 的 Q π ( s , a ) Q^π(s,a) Qπ(s,a),如此反复迭代,Actor π π π就会越来越好。
- 更好 的含义是指:对于任意一个state s i s_i si,都满足: V π ′ ( s i ) ≥ V π ( s i ) V^{π'}(s_i)≥V^{π}(s_i) Vπ′(si)≥Vπ(si),即当Actor的轨迹走到任意一个 s i s_i si 的时候,用 π ′ π' π′ 继续跟环境互动下去得到的 Reward 都要大于等于用 π π π 继续跟环境互动下去得到的 Reward。
- 根据
Q
π
(
s
,
a
)
Q^π(s,a)
Qπ(s,a) 值 寻找
π
′
π'
π′ :
π ′ ( s ) = arg max a Q π ( s , a ) π'(s)=argmax_aQ^π(s,a) π′(s)=argamaxQπ(s,a) - 根据 π ′ ( s ) = arg max a Q π ( s , a ) π'(s)=argmax_aQ^π(s,a) π′(s)=argmaxaQπ(s,a) 决定 π π π 的 action 的步骤,就是 π ′ π' π′。即:当 π π π 根据采样数据 learn 得出一个 Q π ( s , a ) Q^π(s,a) Qπ(s,a),则在某一个 state s i s_i si 状态时,把所有可能的 action a k a_k ak 都分别代入 Q π ( s , a ) Q^π(s,a) Qπ(s,a) 这个 Function,可以让 Q π ( s , a ) Q^π(s,a) Qπ(s,a) 的值最大的 action a k a_k ak 就是 π ′ π' π′ 会采取的 action。可见, π π π 在 state s i s_i si 状态时采取的 action a j a_j aj 与 π ′ π' π′ 在 state s i s_i si 状态时采取的 action a i a_i ai 不一定一样。
- 所以实际上,根本就没有实现存在的叫做 π ′ π' π′ 的 actor/policy,这个 π ′ π' π′ 其实就是用 Q π ( s , a ) Q^π(s,a) Qπ(s,a) 这个 function 推出来的,所以并没有另外一个 network 决定 π ′ π' π′ 如何与环境互动,我们只要能有 Q π ( s , a ) Q^π(s,a) Qπ(s,a) 就好,有 Q π ( s , a ) Q^π(s,a) Qπ(s,a) 就可以找出 π ′ π' π′ 。所以说: π ′ π' π′ does not have extra parameters. It depends on Q Q Q。
- 公式 π ′ ( s ) = arg max a Q π ( s , a ) π'(s)=argmax_aQ^π(s,a) π′(s)=argmaxaQπ(s,a) is not suitable for continuous action a a a。 因为离散型的 a a a 可以分别代入 Q π ( s , a ) Q^π(s,a) Qπ(s,a) 来计算最大值。但是连续型的 a a a 则无法使用该公式。
4、证明 V π ′ ( s ) ≥ V π ( s ) V^{π'}(s)≥V^{π}(s) Vπ′(s)≥Vπ(s)
-
当 Q π ( s , a ) Q^π(s,a) Qπ(s,a) 中的 a a a 采取的 action/policy 是 π ( s ) π(s) π(s) 的话,则: V π ( s ) = Q π ( s , π ( s ) ) V^π(s)=Q^π(s,π(s)) Vπ(s)=Qπ(s,π(s))。
-
∵ textbf{∵} ∵ Q π ( s , π ( s ) ) ≤ max a Q π ( s , a ) = Q π ( s , π ′ ( s ) ) begin{aligned} Q^π(s,π(s))≤max_{a}Q^π(s,a)=Q^π(s,π'(s))end{aligned} Qπ(s,π(s))≤amaxQπ(s,a)=Qπ(s,π′(s))
-
∴ textbf{∴} ∴ V π ( s ) ≤ Q π ( s , π ′ ( s ) ) color{violet}{V^π(s)≤Q^π(s,π'(s))} Vπ(s)≤Qπ(s,π′(s))
-
∴ textbf{∴} ∴ 也就是说在某一个 state s s s,如果你按照 actor/policy π π π 一直做下去得到的 reward 一定会小于等于在现在这个 state s s s不按照 π π π 所给你指示的方向做下去,而是故意按照 π ′ π' π′ 的方向走一步(只有在 state s s s 这个地方的第一步按照 π ′ π' π′ 的指示走,接下来的所有步骤还是按照原来的 π π π 的指示走),虽然只有一步之差,但是我们可以按照上面这个式子知道,这个时候得到的 Reward Q π ( s , π ′ ( s ) ) Q^π(s,π'(s)) Qπ(s,π′(s)) 一定会比完全 follow π π π 得到的 Reward Q π ( s , π ( s ) ) Q^π(s,π(s)) Qπ(s,π(s)) 还要大
V π ( s ) ≤ Q π ( s , π ′ ( s ) ) = E [ V π ( s t ) ∣ s t = s , a t = π ′ ( s t ) ] = V π ( s t ) = r t + 1 + V π ( s t + 1 ) E { [ r t + 1 + V π ( s t + 1 ) ] ∣ s t = s , a t = π ′ ( s t ) } ≤ E { [ r t + 1 + Q π ( s t + 1 , π ′ ( s t + 1 ) ) ] ∣ s t = s , a t = π ′ ( s t ) } = E { [ r t + 1 + r t + 2 + V π ( s t + 2 ) ] ∣ . . . } ≤ E { [ r t + 1 + r t + 2 + Q π ( s t + 2 , π ′ ( s t + 2 ) ) ] ∣ . . . } . . . ≤ V π ′ ( s ) begin{aligned} V^π(s)≤Q^π(s,π'(s))&=E[V^π(s_t)|s_t=s,a_t=π'(s_t)]\ &xlongequal{V^π(s_t)=r_{t+1}+V^π(s_{t+1})} E{[r_{t+1}+color{violet}{V^π(s_{t+1})}color{black}{]|s_t=s,a_t=π'(s_t)}}\ &≤E{[r_{t+1}+color{violet}{Q^π(s_{t+1},π'(s_{t+1}))}color{black}{]|s_t=s,a_t=π'(s_t)}}\ &=E{[r_{t+1}+r_{t+2}+color{violet}{V^π(s_{t+2})}color{black}{]|...}}\ &≤E{[r_{t+1}+r_{t+2}+color{violet}{Q^π(s_{t+2},π'(s_{t+2}))}color{black}{]|...}}\ &...\ &≤V^{π'}(s) end{aligned} Vπ(s)≤Qπ(s,π′(s))=E[Vπ(st)∣st=s,at=π′(st)]Vπ(st)=rt+1+Vπ(st+1)E{[rt+1+Vπ(st+1)]∣st=s,at=π′(st)}≤E{[rt+1+Qπ(st+1,π′(st+1))]∣st=s,at=π′(st)}=E{[rt+1+rt+2+Vπ(st+2)]∣...}≤E{[rt+1+rt+2+Qπ(st+2,π′(st+2))]∣...}...≤Vπ′(s) -
由上述推导可见,只有一步之差,你会得到比较大的 reward。如果假设每步都是不一样的,每步通通都是 follow π ′ π' π′ 而不是 π π π 的话,那得到的 Reward 一定会更大。
四、Tips of Q-Learning
所有提到的Tips之间并不是冲突的,所以可以一起使用。
1、Target Network
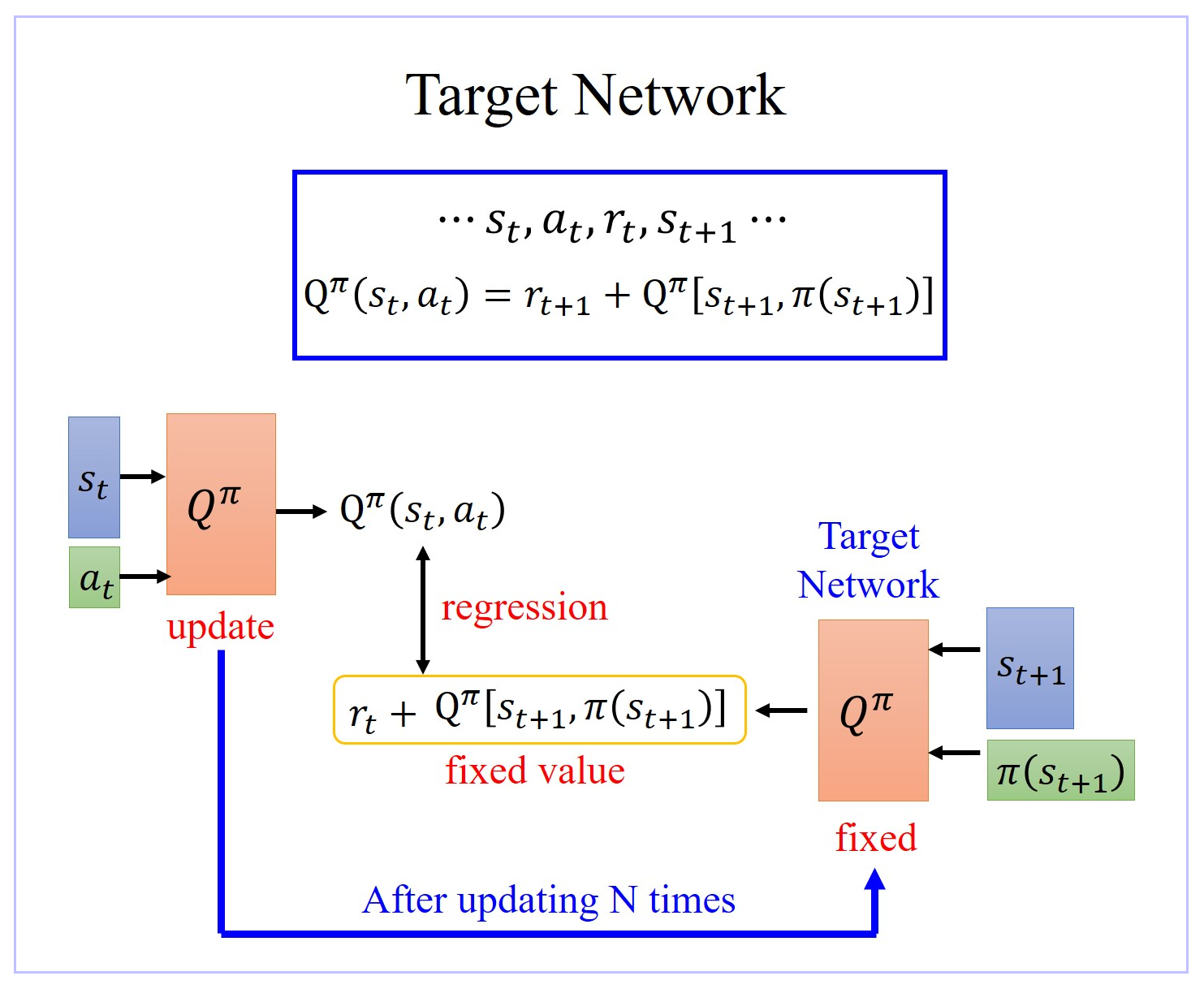
- 在 learn Q π ( s , a ) Q^π(s,a) Qπ(s,a) 过程中,在 state s t s_t st,你采取 action a t a_t at 以后得到 reward r t r_t rt,然后进入下一个 state s t + 1 s_{t+1} st+1,根据 Temporal-difference(TD) approach 方法可知: Q π ( s t , a t ) = r t + 1 + Q π [ s t + 1 , π ( s t + 1 ) ] Q^π(s_t,a_t)=r_{t+1}+Q^π[s_{t+1},π(s_{t+1})] Qπ(st,at)=rt+1+Qπ[st+1,π(st+1)]。 Q π ( s t , a t ) Q^π(s_t,a_t) Qπ(st,at) 与 Q π [ s t + 1 , π ( s t + 1 ) Q^π[s_{t+1},π(s_{t+1}) Qπ[st+1,π(st+1) 之间差了一项就是 r t r_t rt。
- 所以在 learn 的时候,就是将 Q π ( s t , a t ) Q^π(s_t,a_t) Qπ(st,at) function 输入 [ s t + 1 , π ( s t + 1 ) ] [s_{t+1},π(s_{t+1})] [st+1,π(st+1)] 得到的值与输入 ( s t , a t ) (s_t,a_t) (st,at) 得到的Output 之间的差尽可能接近 r t r_t rt。
- 但是实际上在 learn 的时候,这样的一个 function 并不好 learn。因为假设这是一个 regression 的 problem,假设右边的 Q π Q^π Qπ 是target,你会发现你的 target 是会动的,training 会变得不太稳定。这种一直在变的 target 的 training 其实是不太好 train 的。
- 解决方案:
- 先让Target Network 固定住,也就是说你在 training 的时候,你并不 update 这个 Target Network 的参数,只 update 左边 Target Network 的参数,而右边这个 Q 的参数,它会被固定住。target network 负责产生 target。因为 target network 是固定的,所以你现在得到的 target,也就是 r t + 1 + Q π [ s t + 1 , π ( s t + 1 ) ] r_{t+1}+Q^π[s_{t+1},π(s_{t+1})] rt+1+Qπ[st+1,π(st+1)] 的值也会是固定的。那我们只调左边这个 network 的参数。它就变成是一个 regression 的 problem。我们希望我们 model 的 output,它的值跟你的目标越接近越好,minimize 它的 mean square error 或 minimize 它们 L2 的 distance。问题就转换为 regression 问题。
- 在实操上,一开始这两个 network 是一样的,先让Target Network 固定住,把左边的 Q update 好几次,再去把右边的 Target network 用 update 过的左边的 Q 替换掉。但它们两个不要一起动,他们两个一起动的话,结果会很容易坏掉。用 update 后的 Target network 再一次迭代训练左边的 Q。如此反复迭代。
2、Exploration

- 当我们使用 Q function 的时候,我们的 policy 完全 depend on 那个 Q function。given 某一个 state,你就穷举所有的 a,看看哪个 a 可以让 Q value 最大,它就是你采取的 policy。这样的话你采取的 action 总是固定的。这不是一个好的收集 data 的方式。
- 因为假设我们今天真的要估某一个 Q π ( s , a ) Q^π(s,a) Qπ(s,a),比如在某一个 state s s s,你可以采取的 action 有 a 1 , a 2 , a 3 a_1, a_2, a_3 a1,a2,a3。你要估测在某一个 state 采取某一个 action 会得到的 Q value,你一定要在那一个 state s s s 采取过那一个 action a i a_i ai你才估得出它的 value Q π ( s , a i ) Q^π(s,a_i) Qπ(s,ai),但是如果你没有在那个 state s s s采取过那个 action a i a_i ai,你其实估不出那个 action 的 value Q π ( s , a i ) Q^π(s,a_i) Qπ(s,ai)。
- 所以今天假设你在某一个 state s s s,action a 1 , a 2 , a 3 a_1, a_2, a_3 a1,a2,a3 你都没有采取过,那你估出来的 ( s , a 1 ) ( s , a 2 ) ( s , a 3 ) (s, a_1) (s, a_2) (s, a_3) (s,a1)(s,a2)(s,a3) 的 Q value Q π ( s , a i ) Q^π(s,a_i) Qπ(s,ai) 可能就都是一样的,就都是一个初始值,比如说 0。但是假设你在 state s s s sample 过 action a 2 a_2 a2 了,它得到的值是 positive 的 reward,那么 Q π ( s , a 2 ) Q^π(s,a_2) Qπ(s,a2) 就会比其他的 action 的 reward 都要好。因为 Q-Learning 在采取 action 的时候,就看说谁的 Q value 最大就采取谁,所以之后你永远都只会 sample 到 a 2 a_2 a2,其他的 action 就再也不会被做了。
- 解决方案:
- exploration 的机制:需要让 machine 知道说,虽然 a 2 a_2 a2根据之前 sample 的结果,好像是不错的,但你至少偶尔也试一下 a 1 a_1 a1 跟 a 3 a_3 a3,说不定他们会更好。
- 有两个方法解这个问题,一个是 Epsilon Greedy,另外一个方法叫做 Boltzmann Exploration。
- Epsilon Greedy 的意思是说,我们有 1 − ε 1-ε 1−ε 的机率,通常 ε ε ε 设一个很小的值, 1 − ε 1-ε 1−ε 可能是 90%,也就是 90% 的机率,完全按照 Q function 来决定 action;但是你有 10% 的机率是随机的。通常在实作上 ε ε ε会随着时间递减,也就是在最开始的时候,因为还不知道那个 action 是比较好的,所以你会花比较大的力气在做 exploration。那接下来随着 training 的次数越来越多,已经比较确定说哪一个 Q 是比较好的,你就会减少你的 exploration,你会把 ε ε ε 的值变小,主要根据 Q function 来决定你的 action,比较少做 random。
- Boltzmann Exploration,这个方法就比较像是 policy gradient。在 policy gradient 里面我们说 network 的 output 是一个根据 expect(ed) action space 上面的一个 probability distribution,再根据 probability distribution 去做 sample。那其实你也可以根据 Q value 去定一个 probability distribution,假设某一个 action,它的 Q value 越大,代表它越好,那我们采取这个 action 的机率就越高,但是某一个 action 它的 Q value 小,不代表我们不能试试看它好不好用。所以我们有时候也要试试那些 Q value 比较差的 action。因为 Q value 它是有正有负的,所以你要把它弄成一个机率,你可能就先取 exponential,然后再做 normalize,然后把 Q ( s , a ) Q(s, a) Q(s,a) 指数化,然后再做 normalize,得到的这个机率就当作是你在决定 action 的时候 sample 的机率。
3、Noisy Net(Improved Exploration)

3.1 Epsilon Greedy(Action Space Noise)
- Epsilon Greedy 里面,是在 action 上加 noise。就算是给同样的 state,agent 采取的 action,也不一定是一样的。因为你是用 sample 决定的,given 同一个 state,你如果 sample 到 Q function 的 network,你会得到一个 action;你 sample 到 random,你会采取另外一个 action。
- 所以 given 同样的 state,如果你今天是用 Epsilon Greedy 的方法,它得到的 action,是不一样的。但是实际上在一个真实世界的 policy,给同样的 state,他应该会有同样的响应,而不是给同样的 state,它有时候吃 Q function,有时候又是随机的。所以这是一个比较奇怪的,不正常的 action,是在真实的情况下不会出现的 action。
- Epsilon Greedy 是 noisy 的 action,你只是随机胡乱地 explore 这个环境;
3.2 Noisy Net(Parameter Space Noise)
- Noisy Net里面,是在 Q function 的 network 的 参数 上加 noise,那在整个互动的过程中,在同一个 episode 里面,它的 network 的参数总是固定的,所以看到同样的 state,或是相似的 state,就会采取同样的 action,那这个是比较正常的。这个叫做 state-dependent exploration。也就是说你虽然会做 explore 这件事,但是你的 explore 是跟 state 有关系的。看到同样的 state,你就会采取同样的 exploration 的方式。也就是说你在 explore 你的环境的时候,你是用一个比较 consistent 一致的方式去测试这个环境。
- Noisy Net 是在参数下加 noise,那在同一个 episode 里面参数是固定的,那你就是有系统地在尝试。每次会试说,在某一个 state,我都向左试试看,然后再下一次在玩这个同样游戏的时候,看到同样的 state,你就说我再向右试试看,你是有系统地 explore 这个环境。
| Action Space Noise | Parameter Space Noise |
|---|---|
 |  |
 |  |
4、Experience Replay Buffer(经验池)
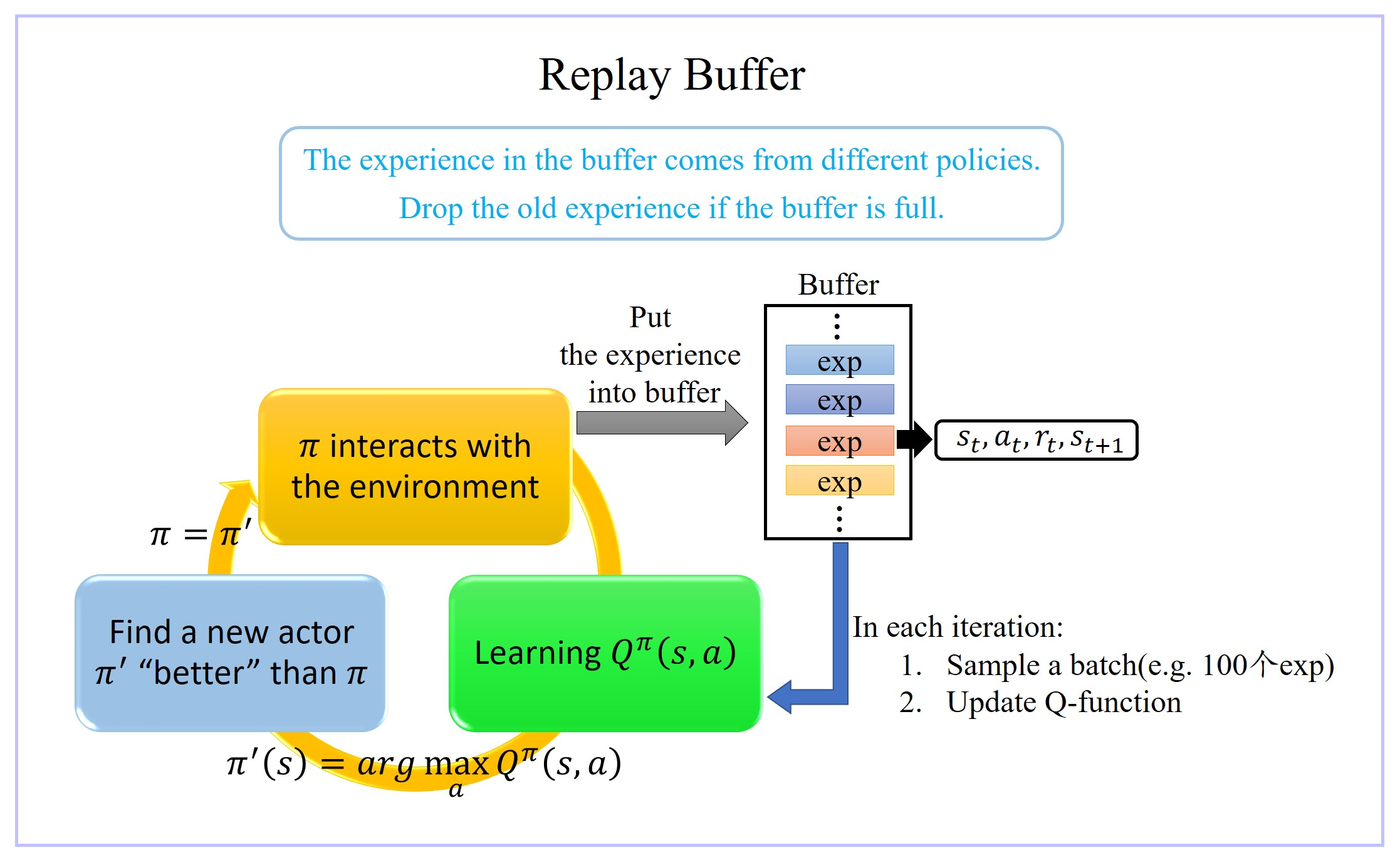
- replay buffer 的意思是说:现在我们会有某一个 policy pi 去跟环境做互动,然后它会去收集 data,我们会把所有的 data 放到一个 buffer 里面,那 buffer 里面就排了很多 data,那你 buffer 设比如说5 万,这样它里面可以存 5 万笔数据。
- 每一笔数据就是记得是之前在某一个 state s t s_t st 采取某一个 action a t a_t at,接下来我们得到的 reward r t r_t rt,然后接下来跳到 state s t + 1 s_{t+1} st+1 这么一个过程。
- π π π 跟环境互动很多次,把所有收集到的数据通通都放到这个 replay buffer 里面,这个 replay buffer 它里面的 experience 可能是来自于不同的 actor/policy π π π,因为每次拿 π π π 去跟环境互动的时候,你可能只互动 10,000 次,然后接下来你就更新 π π π 了,但是你的这个 buffer 里面可以放 5 万笔数据,所以那 5 万笔数据,它们可能是来自于不同更新程度的 π π π。
- buffer 只有在它装满的时候才会把旧的资料丢掉。所以这个 buffer 里面它其实装了很多不同更新程度的 actor/policy π π π 所计算出来的不同的 π π π 的 experiences。
- 就跟一般的 network training 一样,从这个 buffer 里面随机挑一个 batch 出来,里面有一把的 experiences,根据这把 experiences 去 update 你的 Q function。
- 实际上存在你的 replay buffer 里面的这些experiences 不是通通来自于 某一个更新程度的
π
π
π,有些是过去其他更新程度的
π
π
π所遗留下来的 experience,因为你不会拿某一个
π
π
π 就把整个 buffer 装满去测 Q function。这个
π
π
π 只是 sample 了一些 data塞到那个 buffer 里面去,然后接下来就让 Q 去 train。所以 Q 在 sample 的时候,它会 sample 到过去的一些数据。这么做有两个好处:
- 第一个好处:其实在做 reinforcement learning 的时候,往往最花时间的 step是在跟环境做互动,train network 反而是比较快的,因为你用 GPU train 其实很快。replay buffer的使用 可以减少跟环境做互动的次数,因为今天你在做 training 的时候,你的 experience 不需要通通来自于某一个 actor/policy π π π,一些过去的 actor/policy π π π 所得到的 experience可以放在 buffer 里面被使用很多次,被反复的再利用,这样让你的 sample 到 experience 的利用是比较 efficient。
- 第二个好处:在 train network 的时候,其实我们希望一个 batch 里面的 data越 diverse 越好。如果你的 batch 里面的 data 通通都是同样性质的,你 train 下去,其实是容易坏掉的。如果你 batch 里面都是一样的 data,你 train 的时候,performance 会比较差,所以我们希望 batch data 越 diverse 越好。如果这个 buffer 里面的那些 experience 通通来自于不同的 policy 的话,那 sample 到的一个 batch 里面的 data 会是比较 diverse 的。
- 但是接下来你会问的一个问题是:我们明明是要观察最新更新的 π π π 的 value,里面混杂了一些不是最新更新的 π π π 的 experience,到底有没有关系?一个很简单的解释,也许这些不同更新程度的 π π π 也没有差别那么多,所以也没有关系,就算过去的 π π π 和最新更新的 π π π 根本不想其实也是没有关系的,今天主要的原因是因为,我们并不是去 sample 一个 trajectory,我们只是 sample 了一笔 experience。
5、Prioritized Experience Reply Buffer
- The data with larger TD error in previous training has higher probability to be sampled.
- 我们原来在 sample data 去 train 你的 Q-network 的时候,你是 uniformly 地从 buffer 里面去 sample data。那这样不见得是最好的,因为也许其中有一些 data 比其他data更加重要,比如做不好的那些 data。假设有一些 data,你之前有 sample 过,而且那一笔 data 的 TD error(所谓 TD error 就是 network 的 output 跟 target 之间的差距)特别大,那一笔 data 说明你在 train network 的时候是 train 的不好。既然比较 train 不好,就应该给它比较大的机率被 sample 到。所以这样在 training 的时候才会考虑那些 train 不好的 training data 多次一点。

6、Multi-step Experience Reply Buffer
- MC 跟 TD 的方法各自有各自的优劣,我们怎么在 MC 跟 TD 里面取得一个平衡呢?使用 “Multi-step Experience Reply Buffer”。
- 在 “Experience Replay Buffer” 里面的每一个 Experience保存的是 “在某一个 state s t s_t st 采取某一个 action a t a_t at,得到 reward r t r_t rt,接下来跳到 state s t + 1 s_{t+1} st+1”。
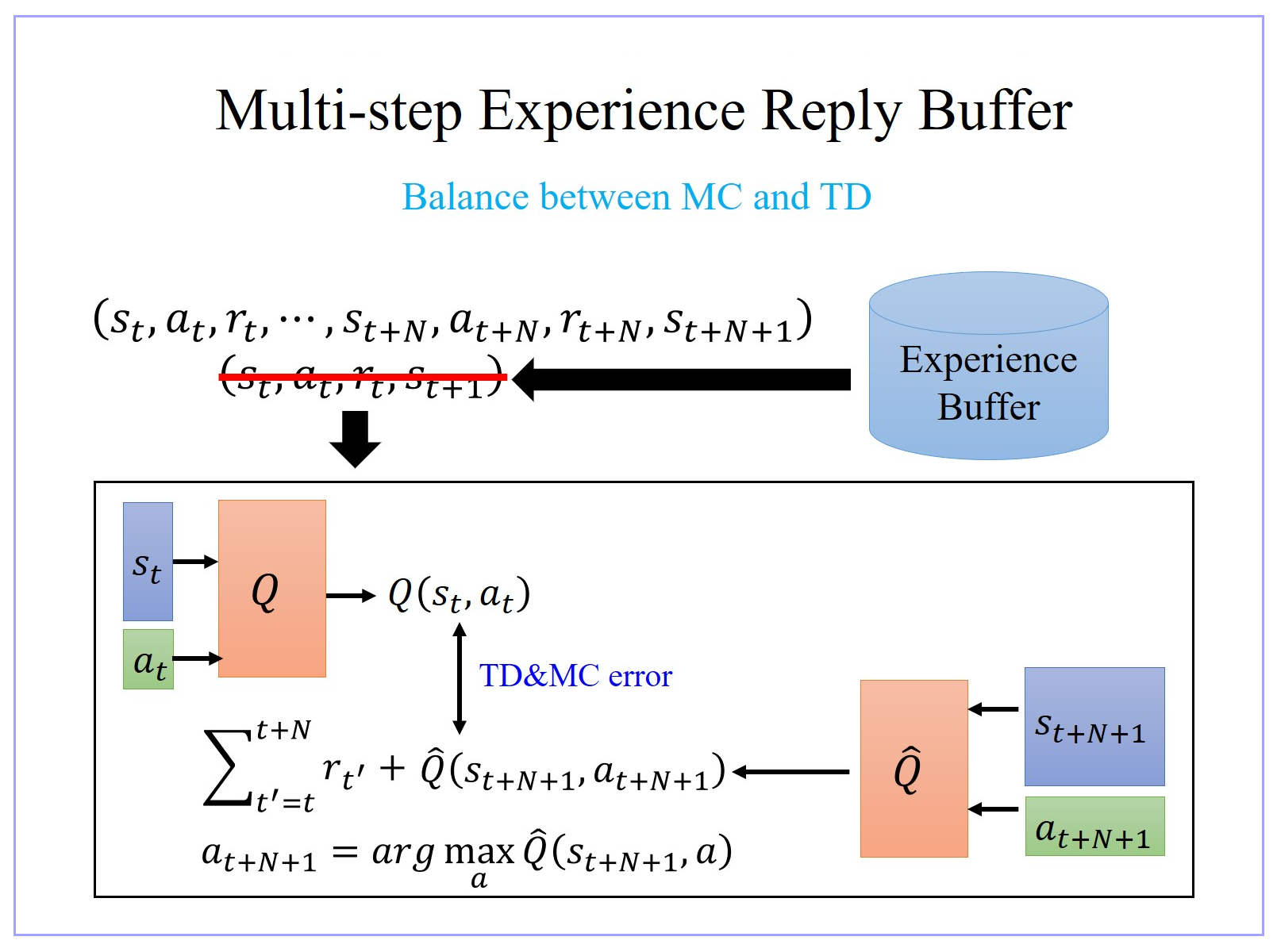
- “Multi-step Experience Reply Buffer” 里的每一个 Experience 保存的不只是一个 step 的 data,而是 N N N 个 step 的 data:“在 s t s_t st 采取 a t a_t at,得到 r t r_t rt,跳到 s t s_t st,一直纪录到在第 N N N 个 step 以后,在 s t + N s_{t+N} st+N 采取 a t + N a_{t+N} at+N 得到 reward r t + N r_{t+N} rt+N”,即从 s t s_t st 跳到 s t + N + 1 s_{t+N+1} st+N+1 的这个经验,通通把它存下来。
- 利用 “Multi-step Experience Reply Buffer” 在做 Q network learning 的时候,要让 Q ( s t , a t ) Q(s_t,a_t) Q(st,at) 跟你 target value 越接近越好。而 target value 是把从时间 t t t 一直到 t + N t+N t+N 的 N N N 个 reward 通通都加起来。 Q ^ hat{Q} Q^ 所计算的,不是 s t + 1 s_{t+1} st+1 状态下的 Q 值,而是 s t + N + 1 s_{t+N+1} st+N+1 状态下的 Q 值。希望 Q ( s t , a t ) Q(s_t,a_t) Q(st,at) 的 target value 跟 s t + 1 s_{t+1} st+1 加上从 s t s_{t} st 到 s t + N + 1 s_{t+N+1} st+N+1 这些步骤的 reward 越接近越好。
- “Multi-step Experience Reply Buffer” 就是 MC 跟 TD 的结合,它就有 MC 的好处跟坏处,也有 TD 的好处跟坏处。
- 好处:因为我们现在 sample 了比较多的 step,之前是只 sample 了一个 step,所以某一个 step 得到的 data 是 real 的,但是接下来都是 Q value 估测出来的。现在 sample 比较多 step,sample N N N 个 step 后才估测 value,所以估测的部分所造成的影响就会比较轻微。
- 坏处:它的坏处就跟 MC 的坏处一样,因为有
N
N
N 项 reward 相加,variance 就会比较大,但是可以去调这个
N
N
N 的值,取得一个平衡。
这就是一个 hyper parameter,你要调这个 N N N 到底是多少(比如:sample 三步还是五步)。
7、Distributional Q-function
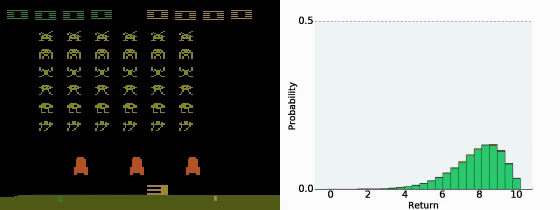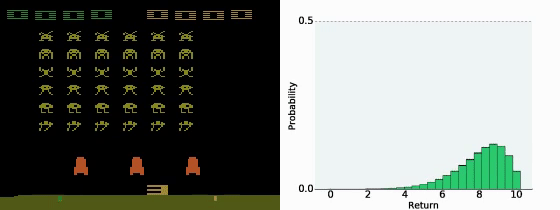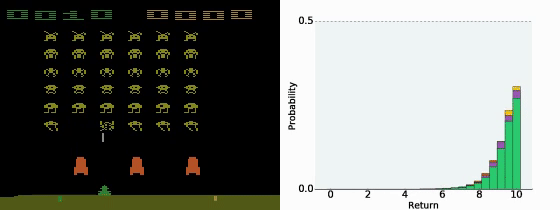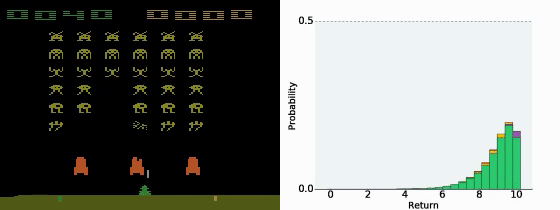
- 状态-行动价值函数 Q π ( s , a ) Q^π(s,a) Qπ(s,a) 是累积收益的期望值,也就是说是价值分布的均值。然而,有的时候不同的分布得到的均值可能一样,但我们并不知道实际的分布是什么。
- Distributional Q-function认为DQN输出的只是 Q π ( s , a ) Q^π(s,a) Qπ(s,a) 的期望,而直接输出分布可能会更好。
- 如果我们知道了 Q π ( s , a ) Q^π(s,a) Qπ(s,a) 的分布,在决策的时候就有更多的选择。例如我们可以在同样的期望的情况下,根据策略更稳健还是更投机选择不同的策略。
- 让模型输出分布,需要给定每一个 Q π ( s , a ) Q^π(s,a) Qπ(s,a) 的上下界,然后类似柱状图一样输出每一个区间的概率。
- Distributional Q-function 认为可以输出 Q π ( s , a ) Q^π(s,a) Qπ(s,a) 值的分布,当具有相同的均值时,选择具有较小方差(风险)的那一个。但实践中这个方法很难付诸实践。
- 使用 Distributional Q-function 不会有 over-estimate的现象,反而有 under-estimate的现象。因为设定的分布范围一般比较窄,所以会忽略掉一些极端值。

A Distributional Perspective on Reinforcement Learning
8、Rainbow
- 把刚才所有的方法都综合起来一起使用就变成 rainbow方法。

五、Q-Learning算法

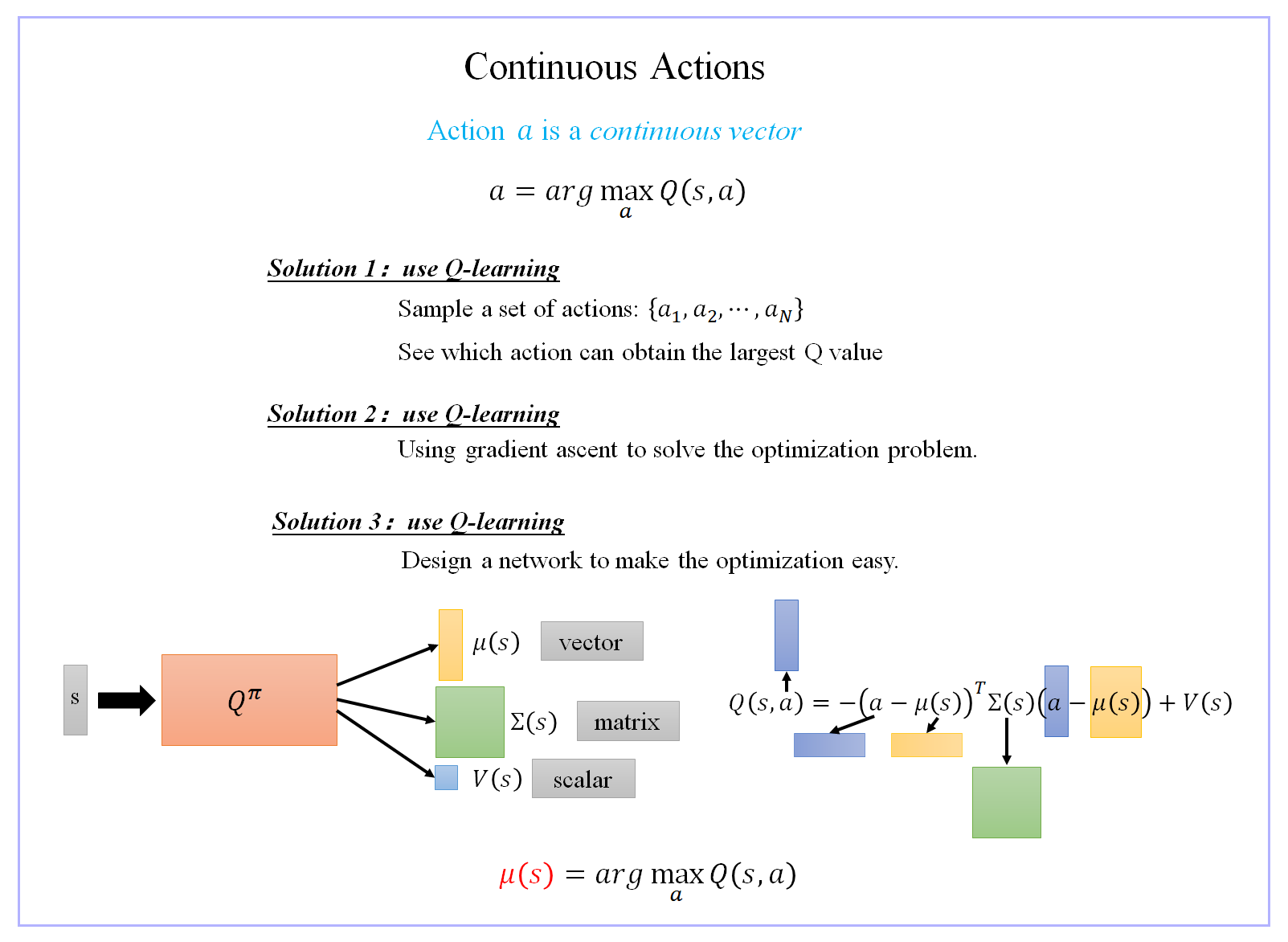
六、处理连续型actions
a = arg max a Q π ( s , a ) a=argmax_aQ^π(s,a) a=argamaxQπ(s,a)
1、使用Q-Learning
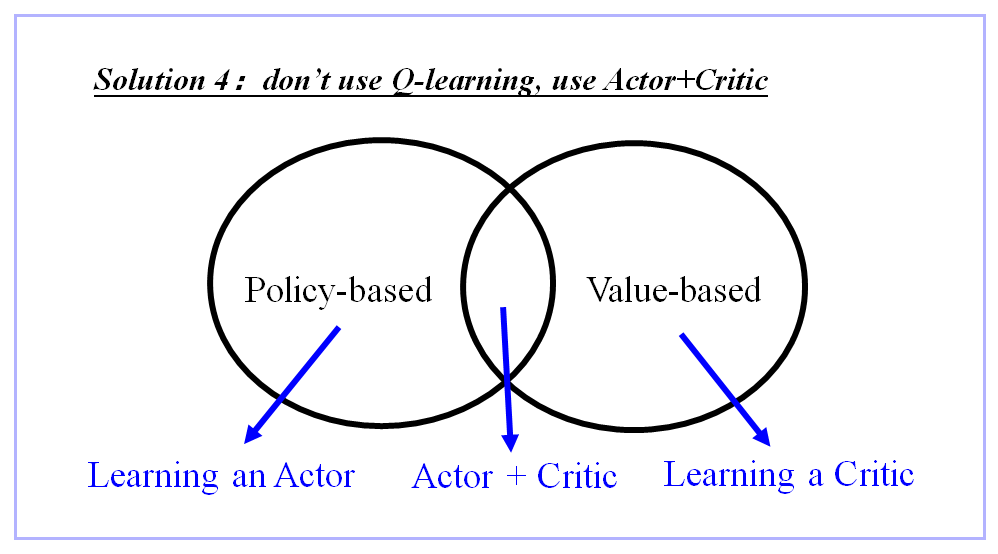
2、使用 Actor+Critic,不使用Q-Learning
参考资料:
Human-level control through deep reinforcement learning
强化学习—DQN算法原理详解
什么是 DQN (强化学习)
DQN(Deep Q-learning)入门教程(一)之强化学习介绍
强化学习系列之九:Deep Q Network (DQN)
Better Exploration with Parameter Noise
A Distributional Perspective on Reinforcement Learning
Rainbow: Combining Improvements in Deep Reinforcement Learning
最后
以上就是自信小兔子最近收集整理的关于人工智能-强化学习-算法:Critic 【用于评价一个 Actor/Policy π】--> Q-Learning【用于训练出来一个最优 Actor/Policy π,擅长处理离散型 actions】一、Critic的作用二、Critic种类三、Q-Learning:从 Q π ( 的全部内容,更多相关人工智能-强化学习-算法:Critic内容请搜索靠谱客的其他文章。








发表评论 取消回复