GAMES101-现代计算机图形学入门（05）笔记-Rasterization 1

延伸一下，在透视投影中的两个概念，如下图：

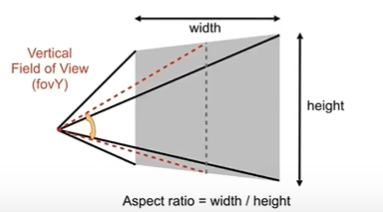
 在上图中，有两个名词概念：一个是长宽比，就是图片最下方的Aspect ratio，类似于我们常说的4:3,16:9的那个意思；

一个是垂直可视角（fovY），就是图片中红色的那一部分。从点出发，到远平面上下的中点的一个连线，在点那形成的角度就叫垂直可视角，主要是来形容在视角的范围。

还可以延伸一个水平可视角，定义类似于上，只是终点变为左右两个中点。

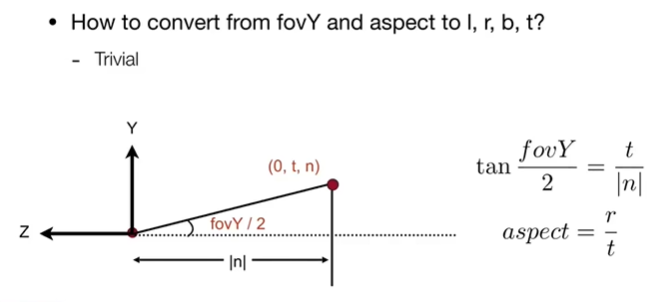
同时，上述的两个概念是可以互相转化并求出的，如下图：在宽高比中，约掉了2

 接下来我们所探讨的是，在上节中，我们知两种投影最后可都变为正交投影来解决。而正交投影的最后就是归到一个（-1,1）的立方体中去解决，那么如何将立方体应用到屏幕中去呢，我们称这种变换为视口变换，也就是下面所要来讨论的。

1、基本定义

像素：抽象的认为每一个屏幕二维数组中的每一个元素。每一个像素是一个方块，且方块内的颜色是统一不变的。

 分辨率：表明有多少像素。

屏幕：是一种典型的光栅成像设备。

 光栅化：理解为，把东西画在屏幕上的过程为光栅化。

三原色：红，绿，蓝。 

2、原理

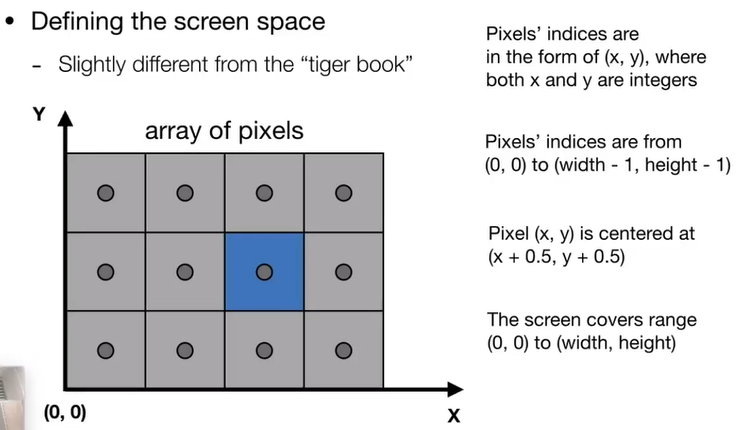
 如下图，将屏幕建立直角坐标系，其中每一个小方块就是上述所说的像素。在建立了直角坐标系后就可以表示出每一个像素的位置，且每一个像素的中心点，就是如图中右边第三条所示。其中，注意，下图中蓝色的小方块的位置为（2,3）：

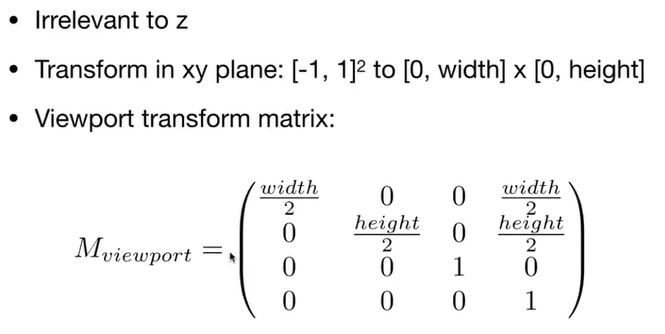
接下来，如何将上述的平面坐标系运用到所说的立方体中呢，就如下图要进行一些变换。首先，（-1,1）的立方体的长度为2，要将其都变为1，所以相应变换的x，y都除以2；然后，要将原点平移到中心，要进行x，y相应的增减变换，也就是如下图矩阵中最右边的一列；z不变：

 在经历上述的变换后，立方体中的像素都有了坐标，就可以清晰的表示出每个像素的位置。

  3、三角形

运用三角形的原因和优势如下图：

 总结上述的图，三角形的优势在于：能代表一个平面；能判断一个点是否在三角形内；而且三角形的三个顶点是可以表示不同的属性的等。

2.1、最简单的光栅化方法：采样

采样：把一个函数离散化的过程，可以理解为：有一个连续的函数，在不同的位置去看这个函数的值为多少。如下图：

主要是对于中心进行采样。

 运用三角形采样，判断中心是否在三角形内，如下图：

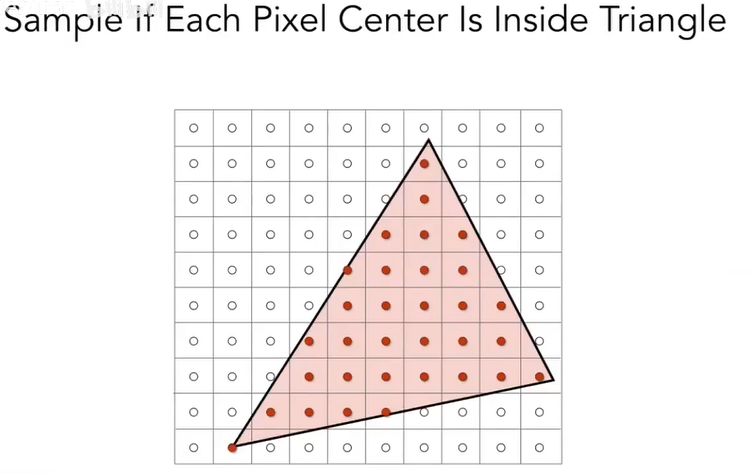
定义 一个inside函数，来判断统计是否在三角形内，在值为1，不在值为0。如下图：

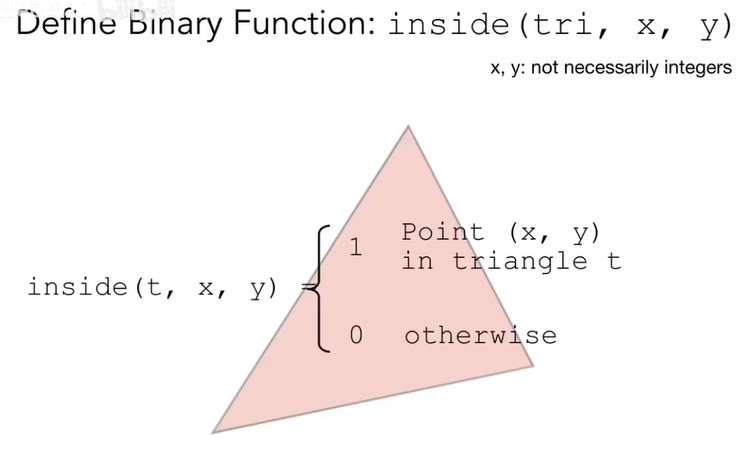
将inside函数运用到来判定中心的方法，如下图： 

那如何来实现，判断中心是否在三角形内呢？就要运用到第一节课Gams101（2）中第三点的叉积的应用就可来判断，主要还是运用右手定则，不赘述，下图：

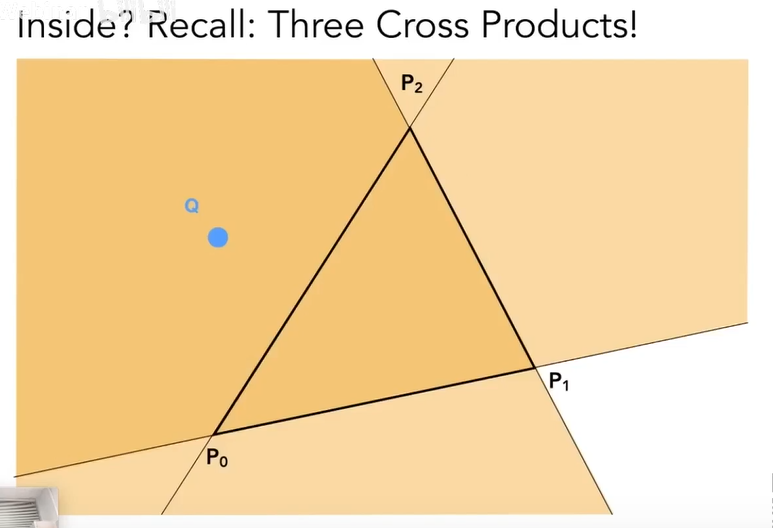
而在一些情况下，可能会出现中心落在三角形的边上，这种情况如何判定因人而异。同时，有项OpenGl的一些会有严格的规定，不需要一定要掌握，了解即可。

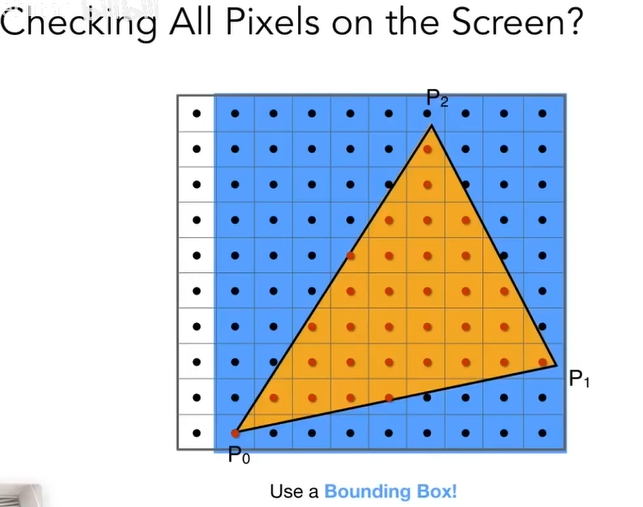
包围盒定义：算是减少无效工作量，下图中最左边的一列就无须在进行三角形采样去计算，计算右边蓝色部分即可。所以包围盒算是光栅化加速的一种方法。

 还有别的光栅化加速的方法，如下图：

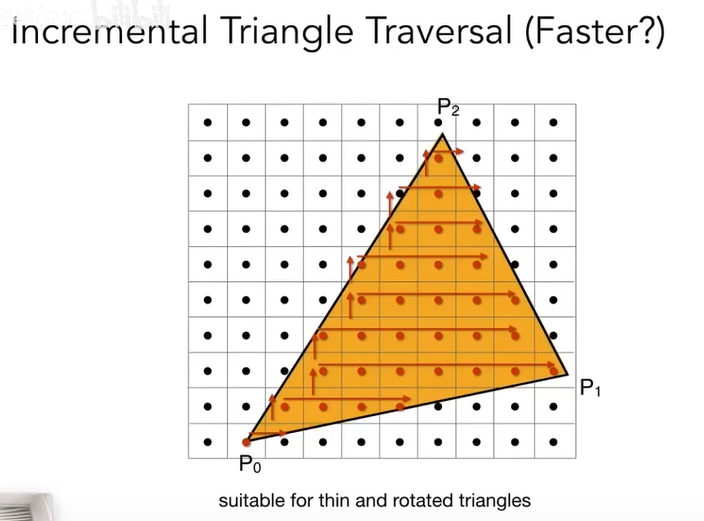
 上图中的原理是寻找每一个最左边和最右边的点作为起始点和终点，再来判断中间的点。

4、延伸

延伸一些问题，如下图：

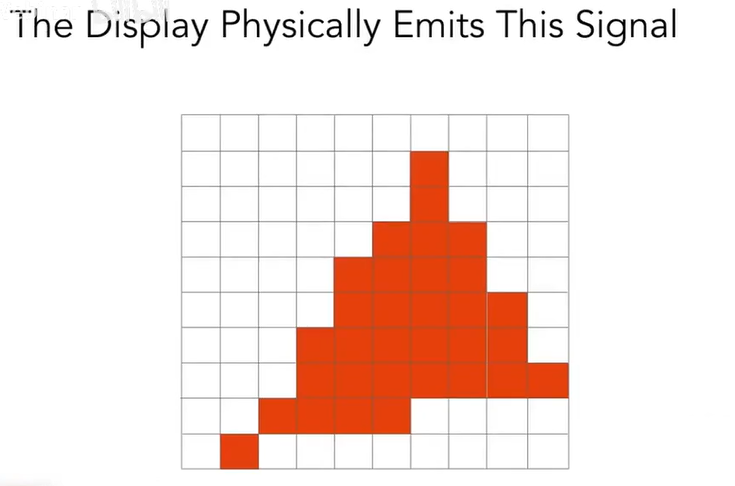
 通过判定好了的中心点来填涂它的像素，就出现了上述的问题。称这个问题叫锯齿问题。

同时，也迎来了图形学中一个重要的解决信号走样的问题：抗锯齿问题

 伴有这图形中常见的走样问题。

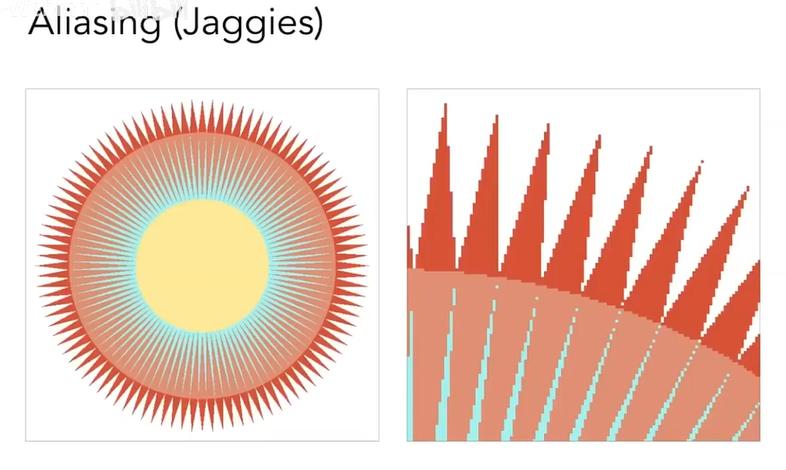
最后

以上就是传统红酒为你收集整理的GAMES101-现代计算机图形学入门（05）笔记-Rasterization 1的全部内容，希望文章能够帮你解决GAMES101-现代计算机图形学入门（05）笔记-Rasterization 1所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。