GAMES101-现代计算机图形学学习笔记（06）

反走样

上一节提到了光栅化三角形，而在实际中，屏幕会由于分辨率和采样频率的一些问题，导致三角形在光栅化过程中出现走样（当然，线条也会出现走样）。这是由于三角形的辺或者线段在观测中是无限细的，可以看做是带宽无限的信号，而对这些图元进行像素化的过程中，采样频率不足，导致采样过程中丢失高频成分，所以产生的信号失真，在屏幕上就表现为锯齿状的图像，这种现象就称为走样，如下图：

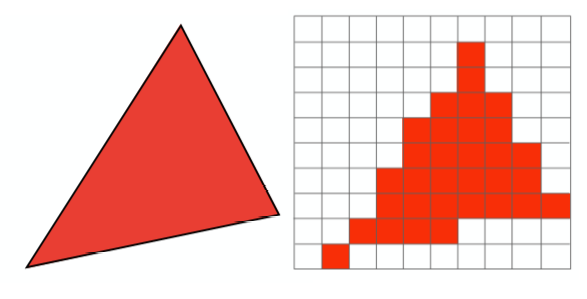
所以我们就需要反走样来减少或消除这种效果。基本上反走样方法可分为两类。第一类是通过提高分辨率即增加采样点(提高采样频率)，比如先在较高分辨率上对光栅进行计算，然后采用某种下采样算法得到较低分辨率的象素的属性，并显示在分辨率较低的显示器上，这类方法有SSAA；另一类反走样是把像素作为一个有限区域，对区域采样来调整像素的颜色或亮度，这种方法类似于图像中的前置滤波（blur等），这类方法有MSAA。

采样伪影(Artifacts)

采样伪影就是由于采样频率不足而产生的一些走样现象。

现实生活中其实也有很多采样伪影出现，比如一段拍摄的视频是由一系列连续帧组成，然而把其中每一帧拿出来看，可以发现其过渡都不是连续的，这就可以看成是在运动过程中拍摄仪器对时间维度的采样频率不足而导致的伪影，如下图：

它的本质是信号变换速度过快，而采样频率不够所产生的。

反走样的一个思想

这里课程提出了一种反走样的思想，即在对信号进行采样之前先对其进行滤波（blur），那么它的结果就会比直接采样好一些，如下两幅图：

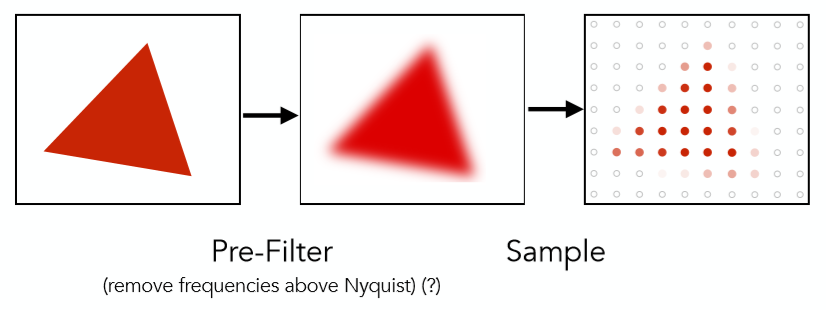
左图为滤波后采样，右图为直接采样：

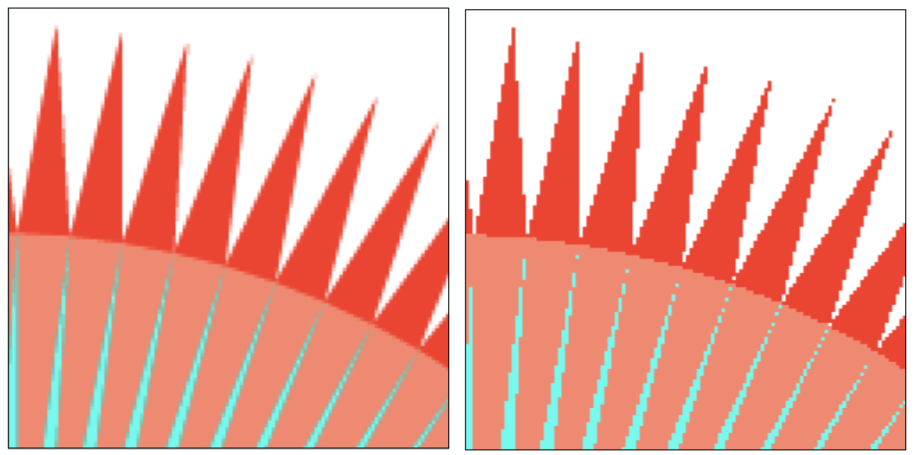
那么为什么会出现这种情况呢？下面课程从频域的角度分析了原因：

频域

我们的世界都是以时间的概念在流逝的，像一首歌一个视频，它是处于时域下的，而频域就是描述信号在频率时用到的一种坐标系，它是另外一种坐标系。而我们常见的正弦波(假定sin 和 cos 都称为正弦波)也是有频率的，如下图：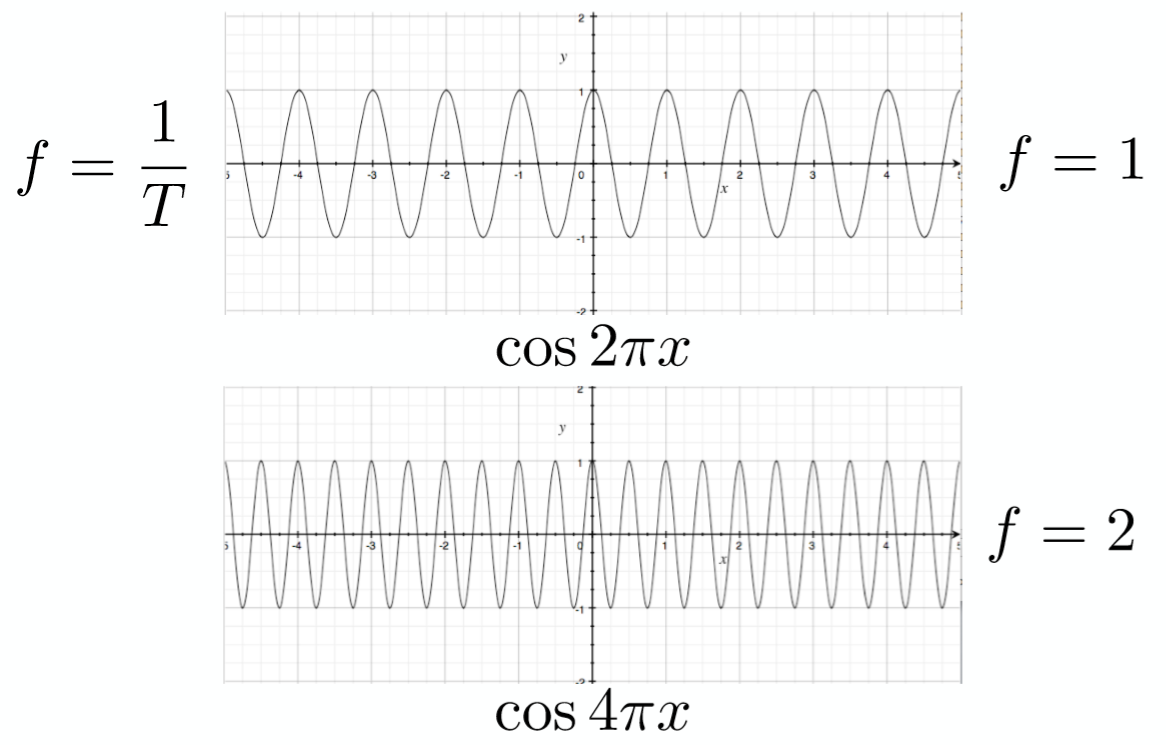

傅里叶变换

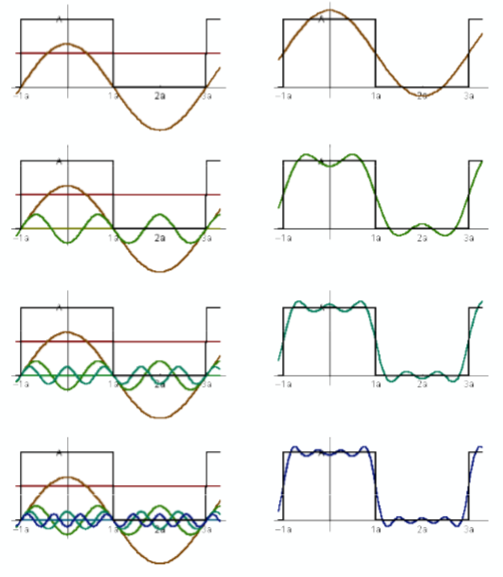
首先要明白傅里叶变换是假设一个函数能够由不同频率的正弦波（cos 和 sin）组合得到。而这里的正弦波，我们把它看做是不同的频率分量，由下图所示：

$$f(x)=\frac{A}{2}+\frac{2A\cos (t\omega )}{\pi }-\frac{2A\cos (3t\omega )}{3\pi }+\frac{2A\cos (5t\omega )}{5\pi }-\frac{2A\cos (7t\omega )}{7\pi }+\cdots$$
上图中随着正弦波的频率的变换，以及数量的增加，可以看到它们的组合逐渐接近一个90°的矩形波。
所以实质上如果想要把一个函数从时域变到频域就可以通过傅里叶变换，而通过其逆变换就可以把这个函数从频域变换到时域，如下图：

这里推荐大家看一篇博文，里面关于频域和傅里叶变换讲得十分清晰：
https://zhuanlan.zhihu.com/p/19763358.

采样与滤波

假设我们以一定的频率对下面的函数进行采样，会发现当函数自身频率越高时，由于采样频率不够，恢复的函数与原来的函数也差异过大。

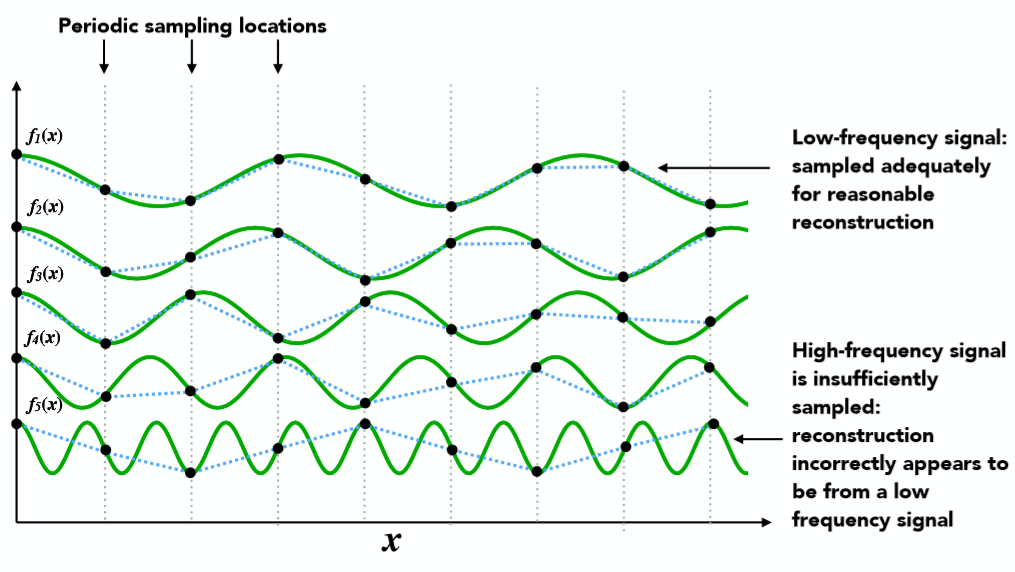
而滤波恰恰就是能够过滤掉图像（函数）中的某些频率部分。如高通滤波，低通滤波。卷积其实也是滤波的一种形式，它是对信号周围进行加权平均的一种运算。而卷积定理在频域与时域上也十分重要，即：
在函数在时域上的卷积等于其在频域上的积，反之亦然，如下图：

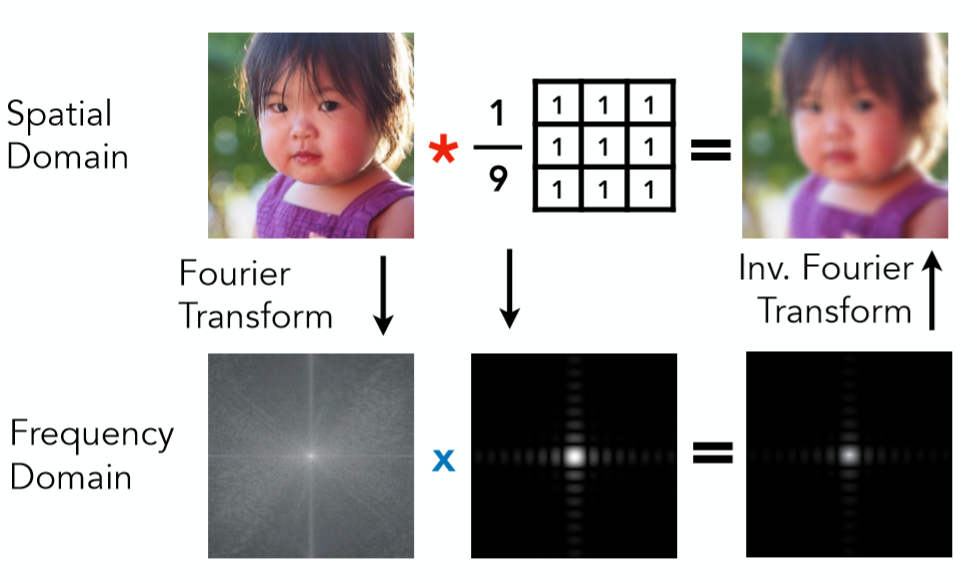
从卷积定理的角度来看采样，其实就可以得出采样实际上是在重复原函数的频域，下图a是原函数，图b是其频域上的形式，我们通过图c的信号对图a进行采样（做乘），本质上就是用图c的频域形式与图a的频域形式做卷积，最后得到的图f结果就是图b的重复（频率的重复）：

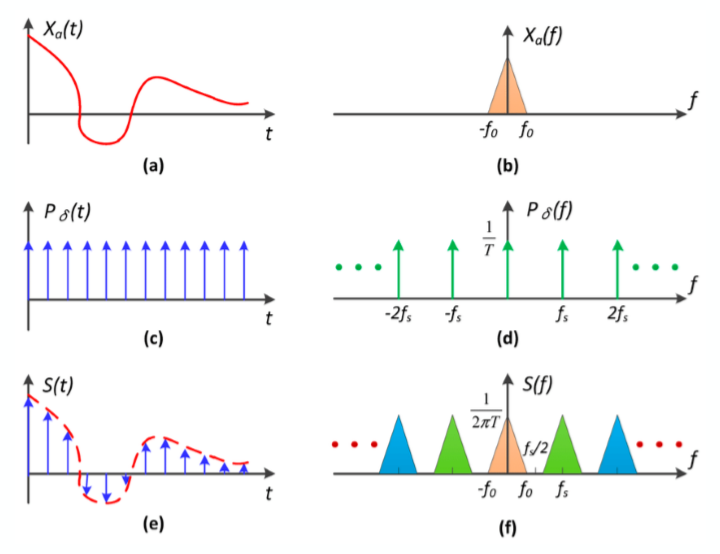
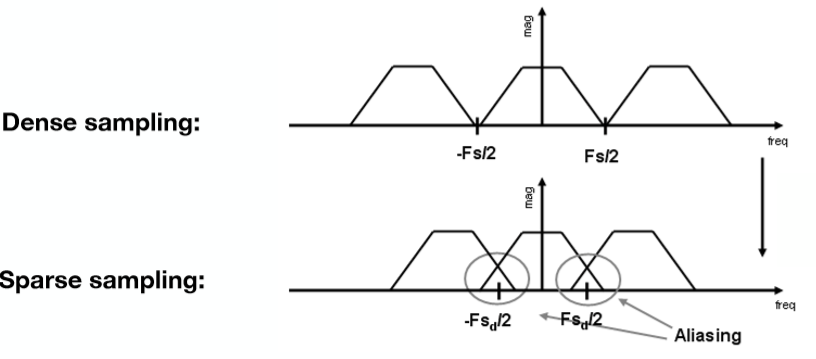
密集采样会把原函数的频域形式分割的较好（恢复得比较好），反之稀疏采样就会恢复得比较差，因为它们的一些频率重复了，这时就会产生走样，如下图：

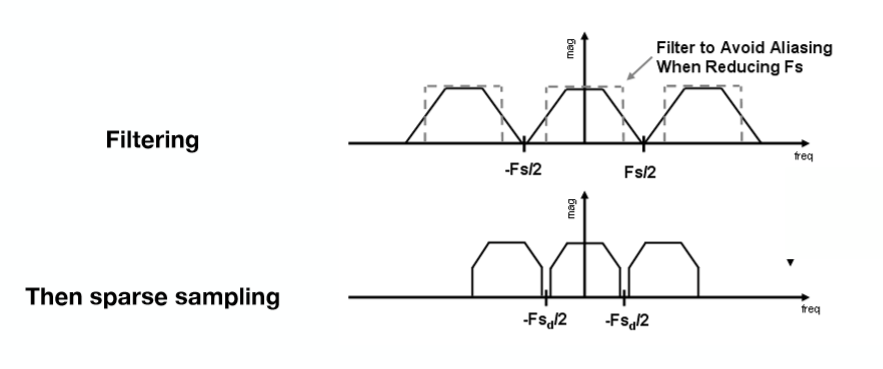
而上面也说了，如果通过滤波把一定范围的频率滤掉，其恢复结果可能就会产生得好一些（即在上图中如果把原函数的低频和高频滤掉）。而模糊本身也是一种滤波，它会把图像中的一些频率去掉，所以这其实也解释了我们在上面可以先滤波，再光栅化，会使得结果更好一些，如下图：

卷积相关

频域上的采样

定义

采样就是重复原始函数在频域的频谱

问题

采样不够快会造成频谱重叠。采样越稀疏，对应频谱的复制会更快，导致重叠更多->走样

通过超采样来反走样(MSAA)

超采样

超采样就是通过对一个像素内的多个位置进行采样并取其平均值来近似1-pixel 滤波器(卷积,blur)的效果
对于4X MSAA来说，其步骤如下：
①假设每个像素中对四个点进行采样
②判断对于一个像素有多少个点在三角形内，然后根据比例对颜色进行"模糊"

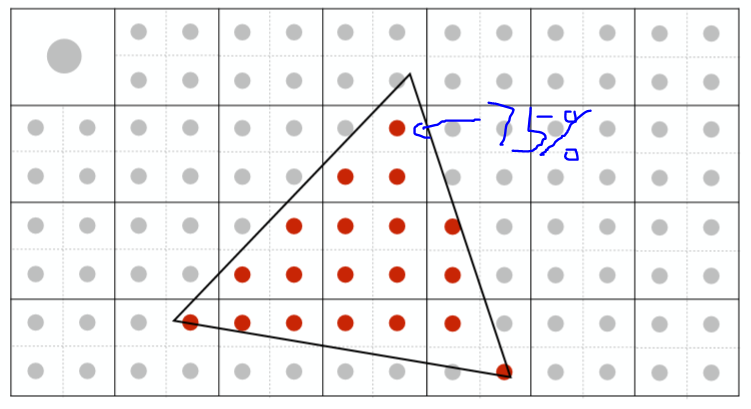
上图中一个像素内的颜色应为原来颜色的 75%。

其他反走样策略

FXAA ，TAA，DLSS等

最后

以上就是机灵手套为你收集整理的GAMES101-现代计算机图形学学习笔记（06）反走样的全部内容，希望文章能够帮你解决GAMES101-现代计算机图形学学习笔记（06）反走样所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。