USACO 2.4 牛的旅行 【最短路Floyed算法】

Time Limit:10000MS Memory Limit:65536K
Total Submit:102 Accepted:68
Case Time Limit:1000MS

Description
　　农民$John$的农场里有很多牧区。有的路径连接一些特定的牧区。一片所有连通的牧区称为一个牧场。但是就目前而言，你能看到至少有两个牧区不连通。这样，农民$John$就有多个牧区了。
　　$John$想在农场里添加一条路径(注意，恰好一条)。对这条路径有以下限制：
　　一个牧场的直径就是牧场中最远的两个牧区的距离(本题中所提到的所有距离指的都是最短的距离)。考虑如下的有$5$个牧区的牧场，牧区用“*”表示，路径用直线表示。每一个牧区都有自己的坐标：
　　
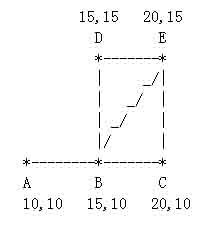
　　这个牧场的直径大约是$12.07106$, 最远的两个牧区是$A$和$E$，它们之间的最短路径是$A-B-E$。
　　这里是另一个牧场：
　　
　　这两个牧场都在$John$的农场上。$John$将会在两个牧场中各选一个牧区，然后用一条路径连起来，使得连通后这个新的更大的牧场有最小的直径。
　　注意，如果两条路径中途相交，我们不认为它们是连通的。只有两条路径在同一个牧区相交，我们才认为它们是连通的。

输入文件包括牧区、它们各自的坐标，还有一个如下的对称邻接矩阵：

A B C D E F G H
A 0 1 0 0 0 0 0 0
B 1 0 1 1 1 0 0 0
C 0 1 0 0 1 0 0 0
D 0 1 0 0 1 0 0 0
E 0 1 1 1 0 0 0 0
F 0 0 0 0 0 0 1 0
G 0 0 0 0 0 1 0 1
H 0 0 0 0 0 0 1 0
　　输入文件至少包括两个不连通的牧区。
　　请编程找出一条连接两个不同牧场的路径，使得连上这条路径后，这个更大的新牧场有最小的直径。

Input
第$1$行: 一个整数$N(1<=N<=150)$, 表示牧区数
第$2$到$N+1$行: 每行两个整数$X,Y(0<=X,Y<=100000)$, 表示$N$个牧区的坐标。注意每个 牧区的坐标都是不一样的。
第$N+2$行到第$2\ast N+1$行: 每行包括$N$个数字($0$或$1$) 表示如上文描述的对称邻接矩阵。
只有一行，包括一个实数，表示所求答案。数字保留六位小数。

Sample Input
8
10 10
15 10
20 10
15 15
20 15
30 15
25 10
30 10
01000000
10111000
01001000
01001000
01110000
00000010
00000101
00000010

Sample Output
22.071068

解题思路

这题我们可以用到$Floyed$算法
参考最短路径问题(最短路径)(Floyed）.
用$Floyed$求出任两点间的最短路，然后求出每个点到所有可达的点的最大距离，记做$mdis[i]$。（$Floyed$算法）
$r1=max(mdis[i])$
然后枚举不连通的两点i,j，把他们连通，则新的直径是$mdis[i]+mdis[j]+(i,j)$间的距离。
$r2=min(mdis[i]+mdis[j]+dis[i,j])$
$re=max(r1,r2)$
$re$就是所求
$AC$代码

代码

#include<iostream>
#include<cstdio>
#include<cmath>
#include<iomanip>
using namespace std;
const double maxn=2147483647.0;
char c;
int n;
double f[200][200],a[200][3],v[200],ans,ans1;
int main(){
	scanf("%d",&n);
    for(int i=1;i<=n;i++)
		cin>>a[i][1]>>a[i][2];//坐标
	for(int i=1;i<=n;i++)
    {
    	for(int j=1;j<=n;j++)
    	{
    		cin>>c;
    		f[i][j]=maxn;//最大值
    		if(c=='1')
			f[i][j]=f[j][i]=sqrt(abs(a[i][1]-a[j][1])*abs(a[i][1]-a[j][1])+abs(a[i][2]-a[j][2])*abs(a[i][2]-a[j][2]));
			//这是无向图，所以a[i][j]和a[j][i]都要赋值为距离
    	}
    }


    for(int k=1;k<=n;k++)//Floyed代码
	{
		for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
		{
			if((i!=j)&&(i!=k)&&(k!=j)&&(f[i][j]>f[i][k]+f[k][j]))
			f[i][j]=f[i][k]+f[k][j];
		} 
	}


	for(int i=1;i<=n;i++)
	{
		double m=0;
		for(int j=1;j<=n;j++)
		{
			if(f[i][j]>m&&f[i][j]!=maxn)
			m=f[i][j];//这个是求每一个点距离它最远的点的距离
		}
		v[i]=m;
		ans=max(ans,v[i]);//这个是牧区目前的最大直径
	}


	ans1=maxn;
	for(int i=1;i<=n;i++)//枚举两个不连通的点，然后就可以计算新的牧区的直径
	{
		for(int j=1;j<=n;j++)
			if(f[i][j]==maxn&&i!=j)
		ans1=min(ans1,v[i]+v[j]+sqrt(abs(a[i][1]-a[j][1])*abs(a[i][1]-a[j][1])+abs(a[i][2]-a[j][2])*abs(a[i][2]-a[j][2])));
	}
	cout<<setprecision(6)<<fixed<<max(ans,ans1);
	//因为有可能新联通的牧场还没有原来的牧场大，所以还要再取一遍最大值
}

最后

以上就是留胡子大炮为你收集整理的USACO 2.4 牛的旅行 【最短路Floyed算法】的全部内容，希望文章能够帮你解决USACO 2.4 牛的旅行 【最短路Floyed算法】所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。