ACM尺取、二分、三分作业

https://vjudge.net/contest/336579#overview

B、G、H、I有难度；

总结

1、适用范围，二分需要满足单调性；三分则需要有峰值存在。明确二分的是什么，怎么验证；

2、边界，对于某些题边界过大或过小会WA（I题）；

3、精度，二分精度尽量小吧，因为是log级别，所以对时间的影响不大；

4、G ++ 和C ++ 的区别，以后用C ++吧 ；

5、尺取法的关键是l 和 r移动的条件设置，应该满足一定单调性，让l和r移动必须可以满足期望，比如B题存在负数，直接移动则不满足期望，没有单调性，如果全为正数则可以满足期望，满足单调性。

题解

A：需要用到map来记录每个数字出现的次数；白书用set来记录数字个数，直接用map记录即可；

首先找到所有出现过的数字，记录l和r，然后先右移l，直到遇到一个在当前序列中只出现过一次的数字（之前弹出的至少出现过两次），将此数字从序列中拿出（l ++），然后更新r值，直到再次遇到这个数，更新答案。

B：好题,有了负数，显然不满足单调性，那么考虑转化，使其满足单调性（是l和r移动的条件清晰）。先求一个前缀和，注意题目要求是绝对值，所以|sum[r] - sum[l] | = | sum[l] - sum[r] |（表示l + 1到 r的和），利用这个特性，我们可以将sum从小到大排序，这样就可以满足尺取条件，然后开始更新，注意的是下表为0的sum应该参与排序，如果取到，说明答案为前k项的和，同时记得初始化，最后答案的左区间是l + 1；

C：二分答案验证，主要是精度的处理，由于输出4位小数，那么r - l 的条件要尽量小;

D：本题主要考数学，在cmath中有反三角函数，可以直接调用；

注意在G++下和C++用printf输出double时%后的类型不同，为了避免以后用C++

G++ : printf("%f" , c);

C++ : printf("%lf", c);

E：直接二分验证即可;

F：直接二分验证，但要注意答案的左边界为最大的数，右边界是所有数的和；

G：较难，需要三分；

lmid = l +（r - l）/ 3;

rmid = r -  (r - l)   / 3;

找峰值； 

车尽量左下角贴墙，然后绕墙角走，尽可能拐弯；

然后三分

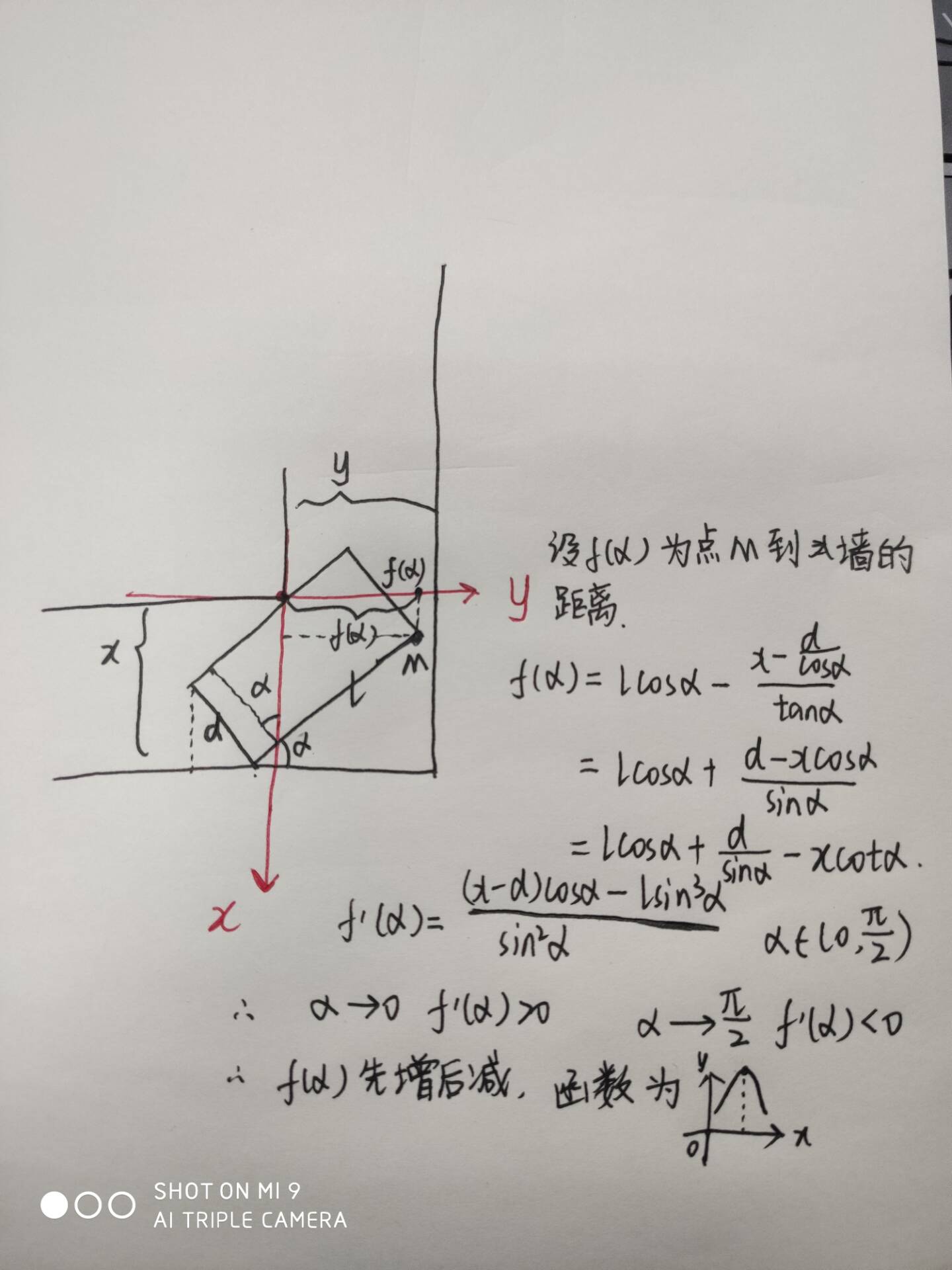
H：数学题，公式推导有些麻烦；

参考：讲的很好，可以直接用公式求出来；

https://blog.csdn.net/weixin_30740295/article/details/95271478

I：好题，先从小到大排序，二分答案，验证前k个数和后k个数的差是否满足答案，要注意边界问题，r取n / 2；

J：用lower_bound即可；

代码

A：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<map>
using namespace std;
map<int,int>ma;
int n,l = 1,r = 1,ans = 2147483647,cnt,sum = 1;
int a[1000001 + 55];

void solve()
{
	cin >> n;
	for(int i = 1;i <= n;i ++)
	{
		scanf("%d",&a[i]);
		if(!ma[a[i]]) ma[a[i]] = 1,cnt ++;
	}
	ma.clear();
	ma[a[l]] ++;
	while(r <= n && l <= r)
	{
		while(sum != cnt && r <= n)
		{
			r ++;
			if(!ma[a[r]]) sum ++;
			ma[a[r]] ++;
		}
		if(sum != cnt || r > n) break;
		ans = min(ans , r - l + 1);
		while(ma[a[l]] >= 2 && l <= r)
		{
			ma[a[l]]--,l ++;
			ans = min (ans,r - l + 1);
		}
		ma[a[l]] --;
		l ++;
		sum --;
	}
	cout << ans;
	return;
}

int main()
{
	solve();
	return 0;
}

B：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;

const int MAXN = 100000 + 55;
int n,m,t,x,l,r,ld,rd;
struct hh {int d,pos;}sum[MAXN];
bool cmp(hh a,hh b) {return a.d < b.d;}

void solve()
{
	sum[0].d = sum[0].pos = 0;
	for(int i = 1;i <= n;i ++)
	{
		cin >> x;
		sum[i].d = sum[i - 1].d + x;
		sum[i].pos = i;
	}
	sort(sum,sum + n + 1,cmp);
	while(m --)
	{
		l = 0,r = 1;
		cin >> t;
		int ans,s = 2147483647;
		while(l <= n && r <= n)
		{
			int summ = abs(sum[r].d - sum[l].d);
			if(abs(summ - t) < s) 
			{
				s = abs(summ - t);
				ans = summ;
				ld = sum[l].pos;
				rd = sum[r].pos;
			}
			if(summ > t) l ++;
			else if(summ < t) r ++;
			else if(summ == t) break;
			if(l == r) r ++;
		}
		if(ld > rd) swap(ld,rd);
		cout << ans << " " << ld + 1 << " " << rd << endl;
	}
	return;
}

int main()
{
	while(cin >> n >> m && n && m)
	solve();
	return 0;
}

C：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;

int T;
double l,r,x;

double calc(double xx)
{
	if(8 * pow(xx,4) + 7 * pow(xx,3) + 2 * pow(xx,2) + 3 * xx + 6 - x < 0.0) return true;
	else return false;
}

void solve()
{
	cin >> x;
	if(x > 807020306.0 || x < 6.0) 
	{
		cout << "No solution!" << endl;
		return;
	}
	l = 0.0,r = 100.0;
	while(r - l >= 1e-6)
	{
		double mid = (l + r) / 2;
		if(calc(mid)) l = mid;
		else r = mid;
	}
	printf("%.4lfn",r);
	return;
}

int main()
{
	cin >> T;
	while(T --)
	solve();
	return 0; 
}

D：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath> 
using namespace std;

double L,n,c,LL,l,r;
void solve()
{
	while(cin >> L >> n >> c)
	{
		if(L < 0.0 && n < 0.0 && c < 0.0) return;
		LL = (1.0 + n * c) * L;
		l = 0.0,r = L * 0.5;
		while(r - l >= 1e-8)
		{
			double mid = (l + r) / 2.0;
			double R = mid / 2.0 + (L * L) / (8.0 * mid); 
			if( LL > 2.0 * R * asin(L / (2.0 * R)) ) l = mid;
			else r = mid;
		}
		printf("%.3lfn",r);
	}
	return;
}
	
int main()
{
	solve();
	return 0;
 }

E：

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;

int l = 214748363,r,n,L,m,ans;
int a[100001];

bool check(int x)
{
	int cnt = 0,last = 0;
	for(int i = 1;i <= n;i ++)
	{
		if(a[i] - last < x) cnt ++;
		else last = a[i];
	}
	if(cnt <= m) return true;
	else return false;
}

void solve()
{
	cin >> L >> n >> m;
	for(int i = 1;i <= n;i ++) cin >> a[i] ;
	sort(a + 1,a + n + 1);
	r = a[++ n] = L;
	for(int i = 1;i <= n;i ++) l = min(l ,a[i] - a[i - 1]);
	while(l <= r)
	{
		int mid = (l + r) >> 1;
		if(check(mid))
		{
			ans = mid;
			l = mid + 1;
		}
		else r = mid - 1;
	}
	cout << ans << endl;
	return;
} 

int main()
{
	solve();
	return 0;
} 

F：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

int l,r,m,n,ans;
int a[500001];

bool check(int x)
{
	int cnt = 0,sum = 0;
	for(int i = 1;i <= n;i ++)
	{
		if(sum + a[i] > x)
		{
			sum = a[i];
			cnt ++;
		}
		else if(sum + a[i] == x) sum = 0,cnt ++;
		else sum += a[i];
	}
	if(sum) cnt ++;
	if(cnt <= m) return true;
	else return false;
}

void solve()
{
	cin >> n >> m;
	for(int i = 1; i <= n;i ++) cin  >> a[i],r += a[i],l = max(l,a[i]);
	while(l <= r)
	{
		int mid = (l + r) >> 1;
		if(check(mid))
		{
			ans = mid;
			r= mid - 1;
		}
		else l = mid + 1;
	}
	cout << ans << endl;
	return;
}

int main()
{
	solve();
	return 0;
}

G：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
double x, y, l ,d;

double calc(double s)
{
	return l * cos(s) - x / tan(s) + d / sin(s);
}

void solve()
{
	double L = 0.0,R = 3.14159265 / 2.0;
	while(R - L >= 10e-8)
	{
		double mid1 = (2 * L + R) / 3.0;
		double mid2 = (L + 2 * R) / 3.0;
		if(calc(mid1) <= calc(mid2)) 
			L = mid1;
		else 
			R = mid2; 
	}
	if(calc(L) <= y) cout <<"yes" <<"n";
	else cout << "no" << "n";
	return;
}


int main()
{
	while(cin >> x >> y >> l >> d)
	solve();
	return 0;
}

H：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;

double x,y,v,g = 9.8,PI = 3.14159265,ans1,ans2;
int T;
void solve()
{
	bool flag = 0;
	cin >> x >> y >> v;
	double a = g * x * x,b = -x * 2 * v * v,c = y * v * v * 2+ g * x * x; 
	double t = b * b - 4 * a * c;
	if(t < 0) cout << -1 << endl;
	else 
	{
		ans1 = atan((-b - sqrt(t)) / (2 * a));
		ans2 = atan((-b + sqrt(t)) / (2 * a));
		if(ans1 >= 0.0 && ans1 <= PI / 2.0) printf("%.6lfn",ans1); 
		else if(ans2 >= 0.0 && ans2 <= PI / 2.0) printf("%.6lfn",ans2);
		else cout << -1 << endl;
	}
	return;
}

int main()
{
	cin >> T;
	while(T --)
	solve();
	return 0;
}

I：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

int n,z,l,r,ans,sum;
int a[1000001];

bool check(int x)
{
	for(int i = 1;i <= x;i ++)
		if(a[n - x + i] - a[i] < z) return false;
	return true;
} 


void solve()
{
	cin >> n >> z;
	for(int i = 1;i <= n;i ++) cin >> a[i];
	sort(a + 1,a + n + 1);
	l = 0,r = n / 2;
	while(l <= r)
	{
		int mid = (l + r) >> 1;
		if(check(mid))
		{
			ans = mid;
			l = mid + 1;
		}
		else r = mid - 1;
	}
	cout << ans << endl;
	return;
} 


int main()
{
	solve();
	return 0;
}

J：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN = 500001;
long long n,m,x;
long long sum[MAXN];


void solve()
{
	cin >> n >> m;
	for(int i = 1;i <= n;i ++) 
		cin >> x,sum[i] = sum[i - 1] + x;
	for(int i = 1;i <= m;i ++)
	{
		cin >> x;
		long long pos = lower_bound(sum + 1,sum + n + 1,x) - (sum);
		cout << pos <<" "<<x - sum[pos - 1] << endl; 
	}
	return;
}

int main()
{
	solve();
	return 0;
}

最后

以上就是纯情耳机为你收集整理的ACM尺取、二分、三分作业的全部内容，希望文章能够帮你解决ACM尺取、二分、三分作业所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。