Gibbs Sampler

54 阅读 0 评论 36 点赞

我是靠谱客的博主害羞跳跳糖，最近开发中收集的这篇文章主要介绍Gibbs Sampler，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

Example: Sampling from a bivariate a Normal distribution

目标函数p(x)是一种规范化形式，表示如下：

均值是:

方差是:

为了使用吉布斯采样从这个分布中采样，我们需要有变量/维度x1和x2的条件分布：

是第二个维度的前一个状态，是从

中得到的第一个维度的状态。有差异的原因是更新x1和x2用的是(t-1)和t时刻的状态，在上一节中的算法大纲第三步可以看出来。第t次迭代，我们首先以变量x2的最近状态即第(t-1)次迭代结果为条件，为x1采样一种新状态。然后再以第t次迭代得到的x1的最新状态为条件采样得到变量x2。

经过一些数学推导(http://fourier.eng.hmc.edu/e161/lectures/gaussianprocess/node7.html)，我们发现目标正态分布的两个条件分布是：

每一个都是单变量的正态分布，其中均值依赖条件变量的最近状态的值，方差依赖两个变量之间的目标方差。

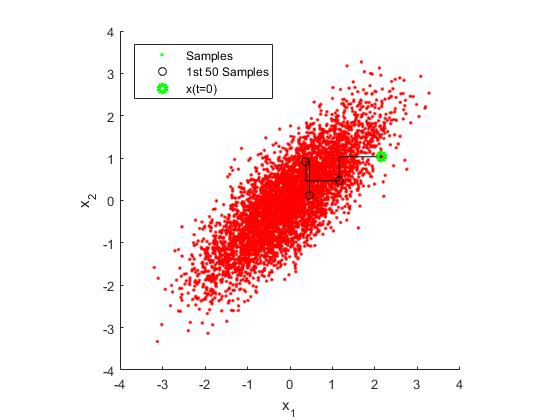
使用上述描述的变量x1和x2的条件概率，我们下面采用matlab实现吉布斯采样，输出的采样如下：

clear all

close all

clc

%seed 用来控制 rand 和 randn

% 如果没有设置seed，每次运行rand或randn产生的随机数都是不一样的

% 用了seed，比如设置rand('seed',0);，那么每次运行rand产生的随机数是一样的，这样对调试程序很有帮助

 
    
         rand( 
         'seed'  
         , 
         12345 
         );     
        
 
         nSamples =  
         5000 
         ;      
        
 
         mu = [ 
         0  
         0 
         ]; % TARGET MEAN目标均值 
        
 
         rho=[ 
         1  
         0.8 
         ; 
         0.8  
         1 
         ];  % 目标方差   
        
 
              
        
 
         %% INITIALIZE THE GIBBS SAMPLER   
        
 
         propSigma =  
         1 
         ; % PROPOSAL VARIANCE   
        
 
         minn = [- 
         3  
         - 
         3 
         ];   
        
 
         maxx = [ 
         3  
         3 
         ];   
        
 
              
        
 
         %% INITIALIZE SAMPLES   
        
 
         x = zeros(nSamples, 
         2 
         );   
        
 
         x( 
         1 
         , 
         1 
         ) = unifrnd(minn( 
         1 
         ), maxx( 
         1 
         ));%unifrnd生成连续均匀分布的随机数   
        
 
         x( 
         1 
         , 
         2 
         ) = unifrnd(minn( 
         2 
         ), maxx( 
         2 
         ));   
        
 
              
        
 
         dims =  
         1 
         : 
         2 
         ; % INDEX INTO EACH DIMENSION  每一维度数组索引 
        
 
              
        
 
         %% RUN GIBBS SAMPLER   
        
 
           
         for  
         t= 
         2 
         :nSamples 
        
 
               
         T=[t- 
         1 
         ,t];      
        
 
               
         for  
         iD= 
         1 
         : 
         2 
        
 
                   
         i=iD+ 
         1 
         ; 
        
 
                   
         if 
         (i> 
         2 
         ) 
        
 
                       
         i= 
         1 
         ; 
        
 
                   
         end 
        
 
                   
         muCond = mu(iD) + rho(i,iD)*(x(T(iD),i)-mu(i));%计算均值=μ( 
         1 
         )+ρ( 
         21 
         )*(x(n, 
         2 
         )-μ( 
         2 
         ))，其中x(n, 
         2 
         )代表样本第n个数据的第二维  
        
 
                   
         var 
         Cond = sqrt( 
         1 
         -rho(i,iD)^ 
         2 
         );%计算方差   
        
 
                   
         x(t,iD) = normrnd(muCond, 
         var 
         Cond);%正态分布随机函数，计算得到当前第t个数据的第 
         1 
         维数据value   
        
 
               
         end 
        
 
           
         end 
        
 
              
        
 
         % DISPLAY SAMPLING DYNAMICS   
        
 
         figure;   
        
 
         h1 = scatter(x(:, 
         1 
         ),x(:, 
         2 
         ), 
         'r.' 
         );%scatter描绘散点图，x为横坐标，y为纵坐标   
        
 
              
        
 
         % CONDITIONAL STEPS/SAMPLES   
        
 
         hold on;%画出前 
         3 
         个采样点   
        
 
         for  
         t =  
         1 
         : 
         3   
        
 
              
         plot([x(t, 
         1 
         ),x(t+ 
         1 
         , 
         1 
         )],[x(t, 
         2 
         ),x(t, 
         2 
         )], 
         'k-' 
         );   
        
 
              
         plot([x(t+ 
         1 
         , 
         1 
         ),x(t+ 
         1 
         , 
         1 
         )],[x(t, 
         2 
         ),x(t+ 
         1 
         , 
         2 
         )], 
         'k-' 
         );   
        
 
              
         h2 = plot(x(t+ 
         1 
         , 
         1 
         ),x(t+ 
         1 
         , 
         2 
         ), 
         'ko' 
         );   
        
 
         end   
        
 
              
        
 
         h3 = scatter(x( 
         1 
         , 
         1 
         ),x( 
         1 
         , 
         2 
         ), 
         'go' 
         , 
         'Linewidth' 
         , 
         3 
         );   
        
 
         legend([h1,h2,h3],{ 
         'Samples' 
         , 
         '1st 50 Samples' 
         , 
         'x(t=0)' 
         }, 
         'Location' 
         , 
         'Northwest' 
         )   
        
 
         hold off;   
        
 
         xlabel( 
         'x_1' 
         );   
        
 
         ylabel( 
         'x_2' 
         );   
        
 
         axis square 
        
 
  