前文链接

软间隔

合页损失函数

线性支持向量机还有另一种解释，最小化目标函数
$$\sum _{i=1}^N[1-y_i(w\cdot x_i+b){]}_{+}+\lambda \Vert w{\Vert }^2$$
其中函数
$$L(y(x\cdot x+b))=[1-y(w\cdot x+b){]}_{+}$$
称为合页损失函数(hinge loss function)，符号$+$表示取函数的正部. 这种损失函数表示只有当样本点$(x_i,y_i)$被正确分类且函数间隔$y_i\cdot (w\cdot x_i+b)$大于1时，损失为0，否则损失为$1-y_i\cdot (w\cdot x_i+b)$

定理：
线性支持向量机原始最优化问题
$$\begin{gathered} \underset{w,b,\xi }{\min }\frac{1}{2}\Vert w{\Vert }^2+C\sum _{i=1}^N{\xi }_i \\ s.t.\{\begin{array}{l}{y}_i(w\cdot x_i+b)\ge 1-{\xi }_i,i=1,2,\dots ,N\\ {\xi }_i\ge 0,i=1,2,\dots ,N\end{array}\text{\hspace{1em}(1)} \end{gathered}$$
等价于最优化问题
$$\underset{w,b}{\min }\sum _{i=1}^N[1-y_i(w\cdot x_i+b){]}_{+}+\lambda \Vert w{\Vert }^2\text{\hspace{1em}(2)}$$
证明：
可以将最优化问题$(2)$转化为$(1)$. 令
$$[1-y_i(w\cdot x_i+b)]={\xi }_i$$
所以有${\xi }_i\ge 0$成立，又因为当$1-y_i(w\cdot x_i+b)>0$时，$1-y_i(w\cdot x_i+b)={\xi }_i$，当$1-y_i(w\cdot x_i+b)\le 0$时，${\xi }_i=0$，所以$y_i(w\cdot x_i+b)\ge 1-{\xi }_i$. 即最优化问题可以写成
$$\underset{w,b}{\min }\sum _{i=1}^N{\xi }_i+\lambda \Vert w{\Vert }^2$$
令$\lambda =\frac{1}{2C}$
$$\underset{w,b}{\min }\frac{1}{C}(\frac{1}{2}\Vert w{\Vert }^2+C\sum _{i=1}^N{\xi }_i)$$
与模型$(1)$等价.
合页损失函数和0-1损失函数图像如下
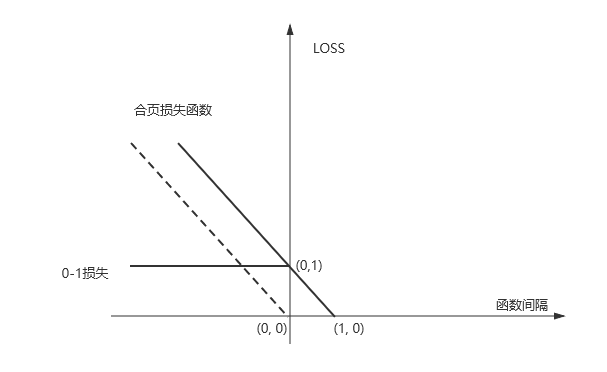可以发现合页损失函数时0-1损失函数的上界，并且由于0-1损失函数不是连续可导的，直接优化目标函数比较困难，可以考虑优化损失函数的上界，这时上界损失函数又被称为代理损失函数（surrogate loss function）.

虚线部分时感知机损失函数
$$[-y_i(w\cdot x_i+b){]}_{+}$$
相比较而言，合页损失函数不仅要求分类正确，还要求一定的函数间隔，损失才能达到0，是一种要求更高的损失函数.

参考资料

统计学习方法 清华大学出版社 李航

最后

以上就是传统楼房为你收集整理的【ML】SVM(4) 合页损失函数前文链接合页损失函数参考资料的全部内容，希望文章能够帮你解决【ML】SVM(4) 合页损失函数前文链接合页损失函数参考资料所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。