关于SVM的合页损失函数与原始最优化问题等价性的证明等价性证明

192 阅读 0 评论 127 点赞

李航老师的书中写的不是很详细，想了一番参考了一下这个博客，终于明白了这个等价性是怎么来的。

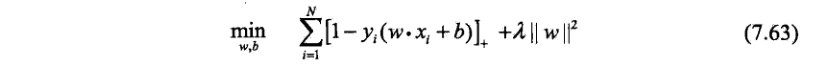
在这里插入图片描述

在这里插入图片描述

等价性证明

书中，令
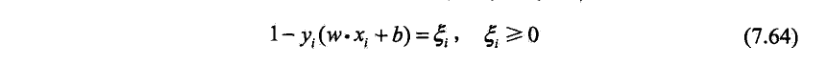
在这里插入图片描述
实际上我觉得这个表述不对，等式应该直接按后文书中给出的，如下表示：
$left[1-y_{i}left(w cdot x_{i}+bright)right]_{+}=xi_{i}, quad xi_{i} geqslant 0 qquad (7.641)$

这里我们分两种情况讨论 $1-y_{i}left(w cdot x_{i}+bright)$ 的取值，当该值大于等于0时候，原等式(7.64)成立。此时，约束(7.61)的等式情况成立

但是该值存在小于0的情况，此时等式(7.64)不成立。但我们注意到，当该值小于0时，实际对应着函数间隔大于1，也就是样本点在正负例的超平面的外侧，该样本点不是支持向量。此时，松弛变量 $xi_i=0$ 。

此时，根据 $1-y_{i}left(w cdot x_{i}+bright)<0$ ， $xi_i=0$ ，可以得到约束(7.61)的不等式情况，至此，约束条件全部成立。

而根据等式(7.641)，代回(7.60)，之后就没有太多的问题了
在这里插入图片描述

以上就是彩色柜子最近收集整理的关于关于SVM的合页损失函数与原始最优化问题等价性的证明等价性证明的全部内容，更多相关关于SVM内容请搜索靠谱客的其他文章。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。