题目描述：

华为用的这个， 其实是个杭电的题目：
题目链接：hdu 3923 Invoker
dota游戏里面，召唤师可以控制冰雷火三种元素，并通过元素组合产生新的技能。现在我们修改了张新的地图， 地图中他能够控制n种元素， 并且将m个元素围成一个圈组成一 个新技能(这m个元素通过旋转或反转，算作重复，如123、231、312、 321、213、 132都算重复)，那么召唤师能组合多少技能(20000>=n>=1 ,1<=m<=10000)，由于结果可能很大，请将结果对1000000007取余

1. 先从n个不同元素里面选择m个元素，得到选择的种类数，
2. 用n个元素去填满m个空位槽，填法通过旋转或者翻转，都算作重复

假设m是3，那么，可以旋转0度，120度，240度
旋转0度：$\left(\begin{array}{ccc}1& 2& 3\\ 1& 2& 3\end{array}\right)$，循环节3
旋转120度：$\left(\begin{array}{ccc}1& 2& 3\\ 3& 2& 1\end{array}\right)$，循环节2，
旋转240度：$\left(\begin{array}{ccc}1& 2& 3\\ 2& 3& 1\end{array}\right)$，循环节1
可以看作用m个元素去填满n个空位，
其实它这里没有说的很清楚，112，322，133 这种包含了相同元素的组合也是可以的，困扰了我非常久，我觉得还是看珠子涂色问题比较清楚
杭电的题目里面详细解释了用例

For Case #1: we assume a,b,c are the 3 kinds of elements.
Here are the 21 different arrangements to invoke the skills
/ aaaa / aaab / aaac / aabb / aabc / aacc / abab /
/ abac / abbb / abbc / abcb / abcc / acac / acbc /
/ accc / bbbb / bbbc / bbcc / bcbc / bccc / cccc /

Output： 输出组合的技能数。

Sample Input
3 4
1 2

Sample Output
Case #1: 21
Case #2: 1

答案来源：https://cloud.tencent.com/developer/article/1179882
不使用欧拉和质数表进行优化的话，会直接TimeOut，
而且面对大数时，有符号数溢出，会直接变成负数，

#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#define MOD 1000000007
#define LL long long
using namespace std;
/***************************************************/
static int prime[30] = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47,
53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101
};
int cnt = 25;
//欧拉公式
LL Eular(LL num)
{
LL ret = 1;
for (int i = 0; i < cnt && prime[i] <= num; i++)
if (num % prime[i] == 0) {
ret *= (prime[i] - 1);
num /= prime[i];
while (num % prime[i] == 0) {
num /= prime[i];
ret *= prime[i];
}
}
if (num > 1)
ret *= (num - 1);
return ret % MOD;
}
//求指数
LL Pow(LL a, LL b) {
LL ret = 1;
while (b) {
if (b & 1)
ret = (ret * a) % MOD;
a = (a * a) % MOD;
b >>= 1;
}
return ret;
}
//Polya公式
LL Polya(int m, int n) {
LL sum = 0, i;
for (i = 1; i * i < n; i++) {
if (n % i == 0) {
sum = (sum + Eular(i) * Pow(m, n / i)) % MOD;
sum = (sum + Eular(n / i) * Pow(m, i)) % MOD;
}
}
if (i * i == n)
sum = (sum + Eular(i) * Pow(m, i)) % MOD;
if (n & 1)
sum = (sum + n * Pow(m, n / 2 + 1)) % MOD;
else
sum = (sum + n / 2 * (Pow(m, n / 2) + Pow(m, n / 2 + 1))) % MOD;
return (sum * Pow(2 * n, MOD - 2)) % MOD;
}
/***************************Polya end****************************/
int main()
{
LL m, n;
LL t, cas = 0;
scanf("%I64d", &t);
while (t--) {
scanf("%I64d%I64d", &m, &n);
//直接调用公式求解
printf("Case #%I64d: %I64dn", ++cas, Polya(m, n));
}
return 0;
}

解析：

使用Polay定理即可，详情看下面解析：

Polya定理：

设有n个对象，G是这n个对象上的置换群，用m种颜色涂染这n个对象，每个对象涂染一种颜色。若一种染色方案在群G的作用下变为另一种方案，则这两种方案当作是一种方案。那么存在的方案个数为 $L$，根据公式：

c(ai)是置换ai的循环节数。
$$m^{c(ai)}=c1(pi)$$

用一个样例来说明下面的4个概念:

1. 置换群G
2. 置换Gi的不动点个数（循环节为1的点数）: $c1(pi)$
3. 循环节：$c(ai)$
4. 着色方案数计算

典例0：对2*2的方阵用黑白两种颜色涂色，问能得到多少种不同的图像

对2*2的方阵用黑白两种颜色涂色，问能得到多少种不同的图像？经过旋转使之吻合的两种方案，算是同一种方案。

1. 若一种染色方案在置换群G的作用下变为另一种方案：
   例如：
   
   正方形C3旋转180度，变成正方形C5 ，说明在旋转180度这个置换下，C3和C5等价、
   可以知道对正方形而言，旋转的情况有，旋转90度，旋转180度，旋转270度，旋转0度， 所以置换群G为： 置 换 群 G = { 旋 转 90 度 ， 旋 转 180 度 ， 旋 转 270 度 ， 旋 转 0 度 } 置换群G={旋转90度，旋转180度，旋转270度，旋转0度} 置换群G={旋转90度，旋转180度，旋转270度，旋转0度}

2. c1(“旋转90度”)是置换旋转90度 的不动点的个数(既循环节为1的点数)：
   例如：
   可知下面的16种情况中：
   
   转90度时，正方形C3转90度可以得到C6的图形，C6转90度得到C5，以此类推，所以(把C6表示为6，C3表示为3)可以写出
   
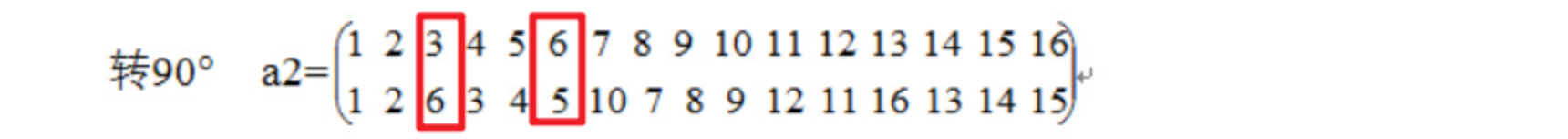
   可以看出：旋转90度时，3可以置换为6，6可以置换为5，5置换为4，4置换为3，回到了3，是一个循环。
   所以，把循环写在一起：（3,6,5,4)(1)(2)(8,7,10,9)(11,12)(13,16,15,14)
   找不动点（循环里只有一个元素的集合），可以看出旋转90度的不动点是(1)、(2)，
   同理：
   转180度时，3可以置换为5，5可以置换为3，是一个循环，
   类似的，有(1)(2)(3,5)(4,6)(7,9)(8,10)(11)(12)(13,15)(16,14)
   所以正方形进行旋转180度的变换时，不动点为(1)(2)(11)(12)
   
   所以，
   旋转0度有16个不动点，
   旋转90度有2个不动点，
   旋转180度有4个不动点，
   旋转270度有2个不动点，

3. 循环节：$c(ai)$
   
   方格可以 旋转 0° , 90 ° , 180 ° ,270° . 所以 群G = { 0° , 90 ° , 180 ° ,270° } , G的阶|G| = 4 ,
   可知
   G1置换{转0° } =$\left(\begin{array}{cccc}1& 2& 4& 3\\ 1& 2& 4& 3\end{array}\right)$
   G2置换{转90° } =$\left(\begin{array}{cccc}1& 2& 4& 3\\ 3& 1& 2& 4\end{array}\right)$
   G3置换{转180° } =$\left(\begin{array}{cccc}1& 2& 4& 3\\ 4& 3& 1& 2\end{array}\right)$
   G4置换{转270° } =$\left(\begin{array}{cccc}1& 2& 4& 3\\ 2& 4& 3& 1\end{array}\right)$
   所以：G1置换（旋转0° ）中，1旋转0° 后得到1，2旋转0° 得到2，3进行G1置换后（旋转0° ）得到3，4置换后得到4，循环节为(1)(2)(3)(4)，总共有4个

   G2置换（旋转90° ）中，
   
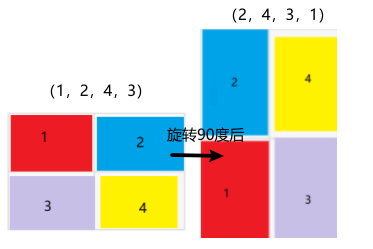
   位置1旋转90° 得到3，位置3旋转90° 得到4，4旋转90° 得到2，2旋转90° 得到1，回到了1，是一个循环。所以：G2置换（旋转90° ）的循环节为（1，3，4，2）
   
   同理： G3置换（旋转180° ）中，1旋转180° 后得到4，4旋转180° 得到1，是一个循环（1，4）；
   2进行G3置换后（旋转180° ）得到3，3置换后得到2，得到循环（2，3）
   循环节为(1，4)(2，3)
   
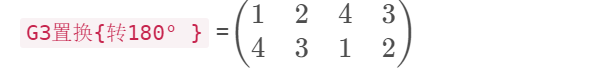
   G1置换{转0° }的循环节是4个。 { (1),(2),(3),(4) }
   G2置换{转90° }的循环节是1， { （1，3，4，2） }
   G3置换{转180°}的循环节是2， { (1,4),(2,3) }
   G4置换{转270°}的循环节是1。 { (1,2,4,3) }

4. 着色方案数量计算：
   
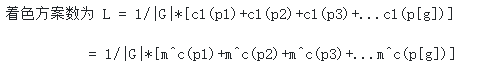
   可知，|G| = 4（对应四种旋转角度）
   置换Gi的不动点个数（循环节为1的点数）:
   $c1(p1:0°)=16,$
   $cl(p2：90°)=2，$
   $cl(p3：180°)=4，$
   $cl(p4：270°）=2$
   置换Gi的循环节个数：
   $c(p1:0°)=4,$
   $c(p2：90°)=1，$
   $c(p3：180°)=2，$
   $c(p4：270°）=1$

   所以
   $L=\frac{1}{|G|}\ast [16+2+4+2]=\frac{1}{|G|}\ast [2^4+2^1+2^2+2^1]=6$

   得到最后方案数 6种。

可以看出，如果要计算 置换Gi的不动点个数（循环节为1的点数）会特别麻烦，所以最好直接通过知道置换Gi的循环节个数来进行计算比较好，那么，怎么求一个置换的循环节数？

1. 方法一：把所有置换写出来，就能知道它们的循环节数了。
2. 方法二：现成公式，对于旋转，有c(ai) = gcd(n,i)，i为转动幅度，1~n，gcd是求最大公约数。

典例1：用2种颜色去染排成一个环的6个棋子

典型题目：用2种颜色去染排成一个环的6个棋子，如果通过旋转得到则只算一种，一共有多少种染色方案？
典型的满足polya公式的条件，m=2，n=6。因为是旋转得到的置换，所以存在6个置换（自己置换到自己也算）。

每个置换的循环节已经标出了。
所以根据polya定理公式可以算出，染色方案数为 $(2^6+2^1+2^2+2^3+2^2+2^1)/6$ = 14

典例2：用m种颜色给n颗珠子染色，经过旋转和翻转的算同一

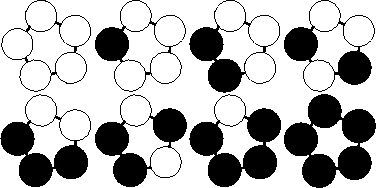
POJ2409：
题意：一家项链公司生产手镯。n颗珠子形成一个环，用m种颜色给n颗珠子染色，就得到了各种各样的手镯。但是，经过旋转和翻转使之吻合的算同一种方案。例如，当用2种颜色对5颗珠子进行染色的方案数为8，
1.对于旋转：有c(gi) = gcd(n,i)，i为转动几颗珠子。gcd是求最大公约数。
2. 对于翻转，当n为奇数时，c(gi) = （n/2）+1；当n为偶数时，n个置换里，有n/2个置换的循环节数为（n/2）+1，有n/2个置换的循环节数为n/2。

所以，计算旋转得到的方案种类数，再计算翻转得到的方案种类数，最后除以（n*2）

计算a,b的最大公约数：

int gcd(int a, int b)
{
return b==0?a:gcd(b,a%b);
}

c++

#include <iostream>
#include <stack>
#include<string>
using namespace std;
typedef __int64 int64;
/***********
* 计算最大公约数
***********/
int gcd(int a, int b) {
return b == 0 ? a:gcd(b, a % b);
}
/*****
* 用m种颜色涂色均匀分布在圆环上的n颗珠子的方案数
******/
int64 polya_circle(double m, int n) {
if (n<0|| abs(m)<0.9999)
{
return 0;
}
int64 result = 0;
// 计算旋转方案数
for (int i = 1; i <=n; i++)
{
result += pow(m, gcd(n, i));
}
// 计算翻转方案数
if (n%2)
{
result += n * pow(m, (n / 2) + 1);
}
else {
result += (pow(m, n / 2) + pow(m, (n / 2) + 1)) * n / 2;
}
return result / n / 2;
}
void Test_polya(int64 result,int64 aim) {
if (result == aim)
{
cout << "pass" << endl;
}
else {
cout << "Failed" << endl;
}
}
void Test_polya_circle() {
Test_polya(polya_circle(2, 5), 8);
Test_polya(polya_circle(1, 1), 1);
Test_polya(polya_circle(5, 1), 5);
Test_polya(polya_circle(2, 6), 13);
Test_polya(polya_circle(6, 2), 21);
}
int main()
{
Test_polya_circle();
}

其他困难例题：

Kaleidoscope(HDU-6360)(Polya定理)
题目大意：给你一个菱形6面体(共60面),然后给你 n nn 种颜色给它每一个面上色，要求第 i ii 种颜色必须至少涂 c [ i ] c[i]c[i] 次,问你本质不同的方案数，旋转相同视作同一种方案，染色方案数对 p pp 取模，多组数据
数据范围：

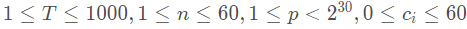
参考：

https://blog.csdn.net/ojshilu/article/details/15378645
http://t.zoukankan.com/bhlsheji-p-4747427.html
https://www.iteye.com/blog/yzmduncan-1402942
https://blog.csdn.net/qq_37555704/article/details/88073792
https://blog.csdn.net/liangzhaoyang1/article/details/72639208

最后

以上就是傲娇野狼为你收集整理的【Polay定理总结】【2019华为笔试】【普通涂色问题 组合数学】召唤师的技能——圆排列，翻转和项链排列题目描述：的全部内容，希望文章能够帮你解决【Polay定理总结】【2019华为笔试】【普通涂色问题 组合数学】召唤师的技能——圆排列，翻转和项链排列题目描述：所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。