MAX MIN（LC统计定界子数组个数）

56 阅读 0 评论 37 点赞

我是靠谱客的博主小巧热狗，最近开发中收集的这篇文章主要介绍MAX MIN（LC统计定界子数组个数），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

这是atcoder的一道原题。贴上这道题目官方的解答：MAX MIN solution
题目描述：
在这里插入图片描述
案例：

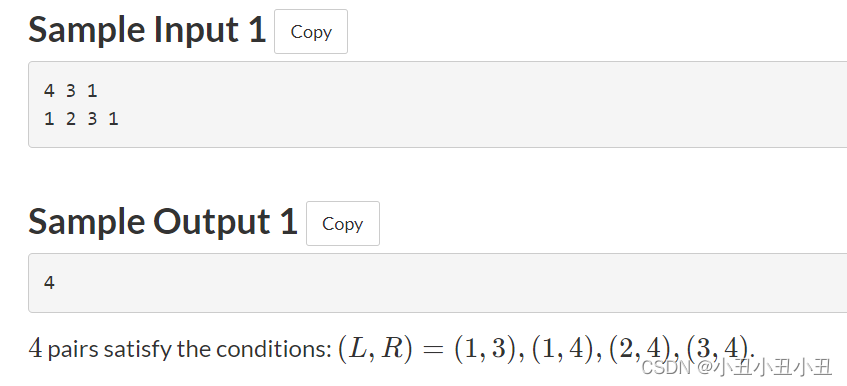
思路：

首先，如果我们用暴力来解答，事件复杂度是 $O(N^3)$ ，很明显会TLE.因此我们要找到一个方法使得事件复杂度是 $O (Nl o g N)$ 或者是 $O (N)$ 。

其次，我们发现一个规律：如果一个数 $A > ma x K an d A < min K$ 那么这一个数肯定就不在合法的区间内了。AtCoder里面给出了一个例子：
在这里插入图片描述

因此我们就可以以这些不合法的（troublesome）的点作为区间的分隔符。分割出来的区域里面的数字一定是 $min K <= x <= ma x K$

因此出现了一个子问题：如何在一段每一个元素范围在 $min K <= x <= ma x K$ 的区间内数出所有包含 $min K$ 和 $ma x K$ 的区间个数呢？

这是一个经典问题，用双指针（或者叫滑动窗口也可以）解决。

思路就是枚举右端点。看一下每一个右端点的离它最近且符合条件的左端点在哪里。（最小符合条件的区间），如果最短的都符合条件了，以该右端点为右端点的所有区间都是符合要求的。

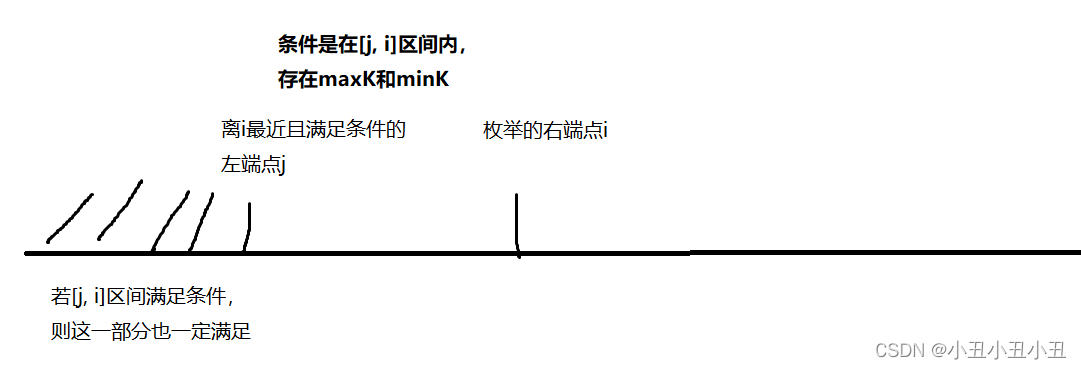
在这里插入图片描述

本题思路结束。

代码：

处理上：

可以先把每一个不合法的点找到然后分割成一段一段合法的区间，再对每一段区间进行双指针搜索。
也可以在双指针搜索的过程当中，遇到不合法的点就进行跳过操作。

第一种方法的代码:

long long countSubarrays(vector<int>& nums, int minK, int maxK) {
        int n = nums.size();
        long long res = 0;
        auto f = [&](int l, int r) {
        	区间内等于minK的元素数量和等于maxK的元素数量
            int smin = 0, smax = 0;
            for(int i = l, j = l, last = l; i <= r; i++) {
            	不需要跳过非法点了，因为非法点已经被我们提前处理掉了
                // if(nums[i] < minK || nums[i] > maxK) {
                //     j = last = i + 1;
                //     smin = smax = 0;
                //     continue;
                // }
                右端点的数如果满足条件，计数加1
                if (nums[i] == minK) smin ++ ;
                if (nums[i] == maxK) smax ++ ;
				
				找离右端点最近的左端点
                while(j <= i) {
                	如果左端点等于minK或者maxK，计数--
                    if(nums[j] == minK) smin--;
                    if(nums[j] == maxK) smax--;
                    如果此时minK或者maxk等于0了，代表如果j右移，这段区间将不符合条件（因为没有数等于minK或者maxK了）
                    if(!smin || !smax) {
                    	j不能右移，把计数加回去
                        if(nums[j] == minK) smin++;
                        if(nums[j] == maxK) smax++;
                        跳出循环，代表j不能移动了，已经是离i最近的左端点了
                        break;
                    } 
                    可以右移就右移
                    j++;
                }
				
				一个右端点已经被枚举完成，可以把以当前i为右端点的所有满足条件的区间数量加到答案里
                if(smin && smax) res += j - last + 1;
            }
        };
        int l = 0, r = 0;
        for(int i = 0; i < n; i++) {
        	如果这个点不合法
            if(nums[i] < minK || nums[i] > maxK) {
                合法区间的右端点
                r = i - 1;
                f(l, r);
                l = i + 1;
            }
        }
        最后还有一段合法区间
        f(l, n - 1);
        return res;
    }

方法2的代码：

long long countSubarrays(vector<int>& nums, int minK, int maxK) {
        int n = nums.size();
        long long res = 0;
        int smin = 0, smax = 0;
        for(int i = 0, j = 0, last = 0; i < n; i++) {
        	遇到不合法的点就跳过，开启一段新的区间
            if(nums[i] < minK || nums[i] > maxK) {
                j = last = i + 1;
                smin = smax = 0;
                continue;
            }

            if (nums[i] == minK) smin ++ ;
            if (nums[i] == maxK) smax ++ ;

            while(j <= i) {
                if(nums[j] == minK) smin--;
                if(nums[j] == maxK) smax--;
                if(!smin || !smax) {
                    if(nums[j] == minK) smin++;
                    if(nums[j] == maxK) smax++;
                    break;
                } 
                j++;
            }

            if(smin && smax) res += j - last + 1;
        }
        return res;
    }