【ML学习笔记】9：认识Decision Tree决策树

简述

决策树的基本思想

决策树算法属于有监督学习，即需要训练集给出各个样本的特征和标签值：

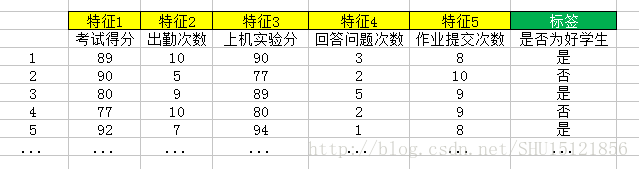
决策树以信息熵及其相关的量为度量指标，构造一棵熵下降最快的树，在叶节点处熵比较小(具体多小也要考虑overfitting的问题)，这时每个叶节点下的实例被认为处于同一类(标签相同)。注意不同叶子下的实例标签未必不同，这在下面的例子里就能看到。
决策树会在每个非叶结点做判别，每个叶结点都是标签的一种取值。每次从根结点走到叶结点，也就是对给定的一个实例的判别路径。通过给定的训练集，构造出的决策树可以是多种多样的：

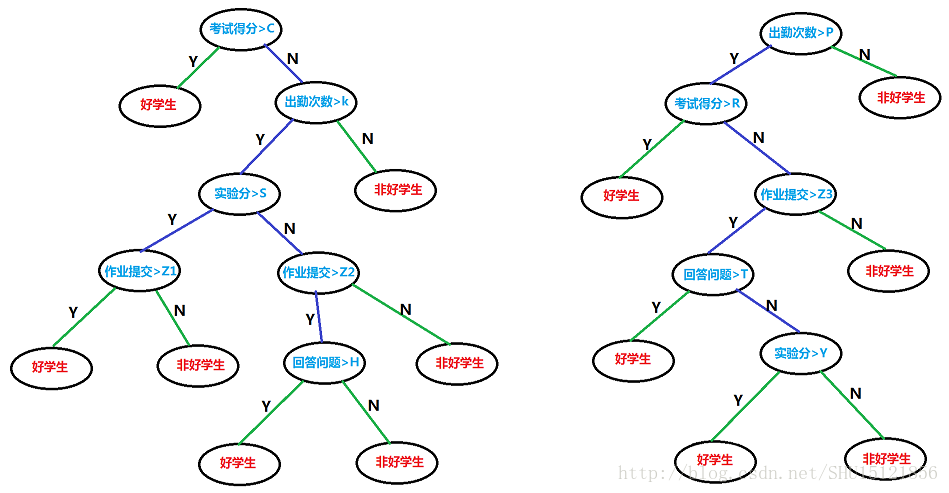
选用什么样的划分方式？从上至下先判断哪个特征，再判断哪个特征？判断时的条件是什么，如果用阈值，阈值取多少？这些都是决策树算法具体使用时要思考的问题。

初识Cross-Validation(交叉验证)

不需要决策树算法得到的学习机器对训练集中的模型全部能正确分类，就如前面所了解到的，这样做可能会导致过度拟合(overfitting，前面用的是过学习这个词)。
像决策树这样的有监督学习算法的评估常常采用交叉验证的方式，即从训练集中拿出大部分数据做训练，而留下一小部分数据做测试，然后轮换着使用，比如4-folds交叉验证即是把样本分成4部分，然后这样4次训练并测试：

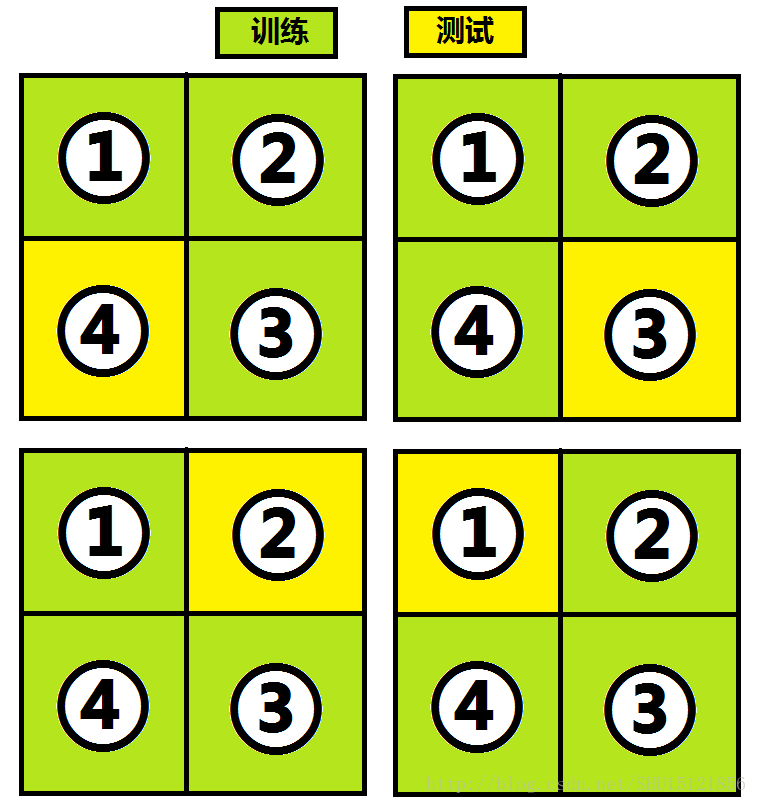
把这样4次测试(如果是k-folds交叉验证那么就是k次)的结果作为对算法可靠性的估计，以表征我们得到的决策树算法性能如何。

自信息量

信息量是对信息多少的一种表征，显然和信息本身是有关系的。而”信息”是”事件发生”的表征，信息可以认为是从信源发出来的一种信号：

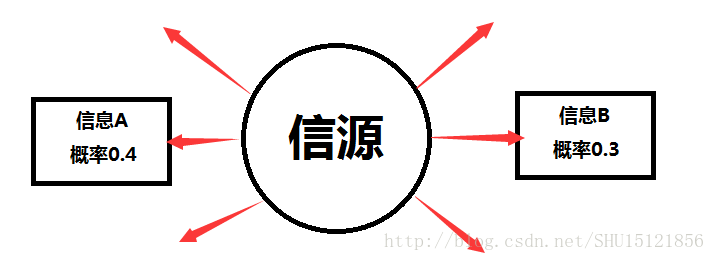
从概率的角度来看，事件发生的概率越小，所包含的信息量也就越大；事件发生的概率越大，所包含的信息量也就越小。

当事件发生的概率是1时候，这个事件发生提供给我们的信息量就是0。试想”太阳照常升起”这件事完全没法引起我们的注意，因为我们认为这件事发生的概率是1；而”卢本伟开挂”这件事却引起了我们的注意，虽然没法准确描述这件事发生的概率是多少，但是之前从来没有发生过(或者说发生了我们也不知道，也就是没有收到过来自信源的信号)，这件事的概率被认为是比较小的，所以这件事发生提供的信息量就很大了。

自信息量是指在收到信源X发出的信号ai之前，收信者对ai的不确定性，用来描述这个事件发生的信息量。

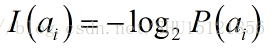
使用ai发生的概率P(ai)的负对数作为自信息量，既满足了前面分析的”发生概率越大信息量越小”，又保证了”在发生概率为1时信息量为0”：

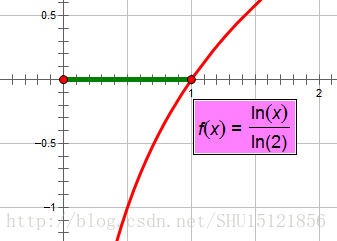
要满足上面的两个条件，其实底数取3，4…什么的也是一样，用换底公式完全可以看出，用不同的底数不过是等价于在前面乘了一个系数：

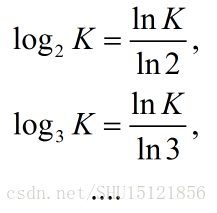
本质上是不影响的，选择2作为底数是遵循信息论的传统习惯。

信息熵

前面说的自信息量，其实是收信者对所有可能事件中某一个事件发生的不确定性，即如果这个事件发生了，那么所获得的信息量。而信息熵就是对于所有可能的事件而言，也就是对于信源可能发出的所有信号，在收到具体的信号之前(即观测到具体的事件发生之前)，对事件发生所能带来的信息量的期望。显然要用每个信号对应的自信息量乘以自己事件发生的概率，再加起来：

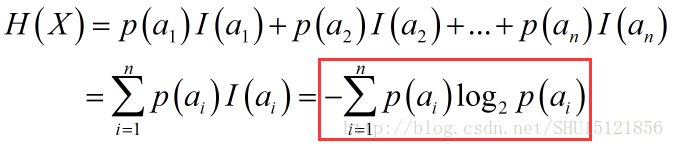
基于n的数目不同，信息熵往往会随着n的增大而增大(当然有时候也不一定)。一般情况下n变大了，也就是说可能发生事件的种类多了，每个事件发生的概率(从整个1那里分到的概率)就少了，取负对数以后即自信息量会大幅增加，最终求得的期望也就是信息熵也会增加，所以信息熵可以表征系统的复杂程度(既考虑出现不同事件的总数n，又考虑各种事件发生的概率分布)。

条件熵

信源还是X，但另外有一个信源Y也能发出信息，接收者能接收它们两个发来的信息。但接收者关注的还是X发来的信息，而Y发来的信息或许对X会发什么信息有参考价值。条件熵H(X|Y)即是描述接收者收到Y发来的每个可能的信息，综合起来对X的不确定估计。也就是X在确定的Y发生的条件下，这个条件概率有关X的信息熵，整体对Y的所有可能的数学期望：

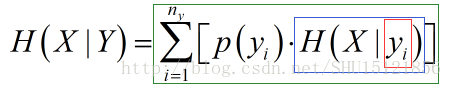
图中红框即是确定的yi发生；蓝框即是在确定的yi发生的条件下X的条件概率的信息熵；绿框即是对于每个yi都存在这样的信息熵，各自乘以p(yi)然后全部加起来，也就是对条件概率的信息熵对Y的所有可能的数学期望。

把里面的信息熵展开，是这样的：

把蓝框外绿框内的那个求期望时用的p(yi)乘进去，因为和j没关系，可以乘到Σ号里面去：

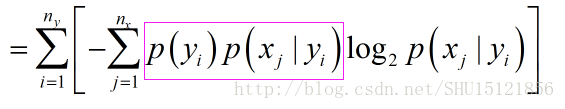
玫红色这一部分还可以用条件概率公式乘到一起，变成：

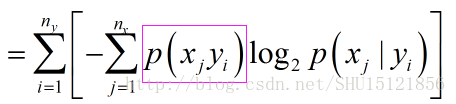
进一步，写成：

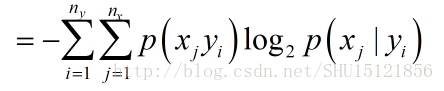
这就是条件熵一般写成的样子。注意条件熵不是在确定的yi发生的情况下X的信息熵，而是对每个可能的yi发生下X的信息熵的数学期望。

平均互信息熵

从前面X的信息熵H(X)和受到Y启发时X的条件熵H(X|Y)知道，可以用它们的差值表征Y所提供给我们的关于X的信息的启发的量，也就是Y所能提供的X的信息量的大小，定义为平均互信息熵：

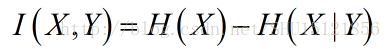
ID3算法

奥卡姆剃刀原理：”如无必要，勿增实体”。能达到同样目的的模型，越简单则推广能力越强。ID3算法(迭代二叉树3代)就建立在这个原理之上。

熵不纯度

在ID3算法生成决策树时，每次选取”分类能力最强的属性”，而用”信息增益”去定义属性的分类能力。自上而下，对于每个要选取属性以作分裂的结点N，先计算与该结点N下剩余的样本有关的熵不纯度(相当于用频率代替概率求得的信息熵)，注意熵不纯度和该结点选取哪个属性(特征及特征的可能取值或划分方式)没关系，只和包含的样本数目及其标签值有关：

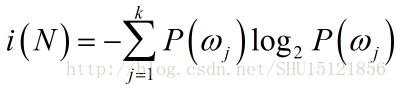
k是结点N下包含的样本的标签的可能取值数目，在二分类问题中就是2,；P(ωj)则是在结点N下，标签是第j种的样本占N下所有样本的频率。

信息增益

计算出结点N处的熵不纯度后，对于这个结点处所有待选的属性A，计算其在该处的信息增益，注意信息增益就和具体选的属性有关系了：

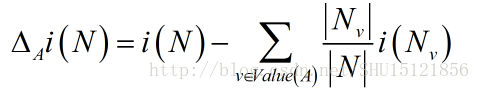
这里v是属性A的每个可能取值，Nv则是结点N下的属性值为具体的v的样本集合。如此去计算每个属性在N处的信息增益，选取信息增益最大的属性在该点做分裂条件，向下递归地去做，就能用ID3算法构造好整个决策树了。

注意，属性和特征不同，当某个特征有离散取值时，属性就是这个特征及其所有可能取值的变量(如天气是晴天/雨天/雪天)；当某个特征有连续取值时，可以设定阈值，则属性就是落在特征及其落在哪个阈值划分好的范围内的变量(如分数是>80/<60/在两者之间)。

一个例子

举一个例子，这个例子是我把书上的天气例子变了个型，可以帮助理解阈值划分属性：

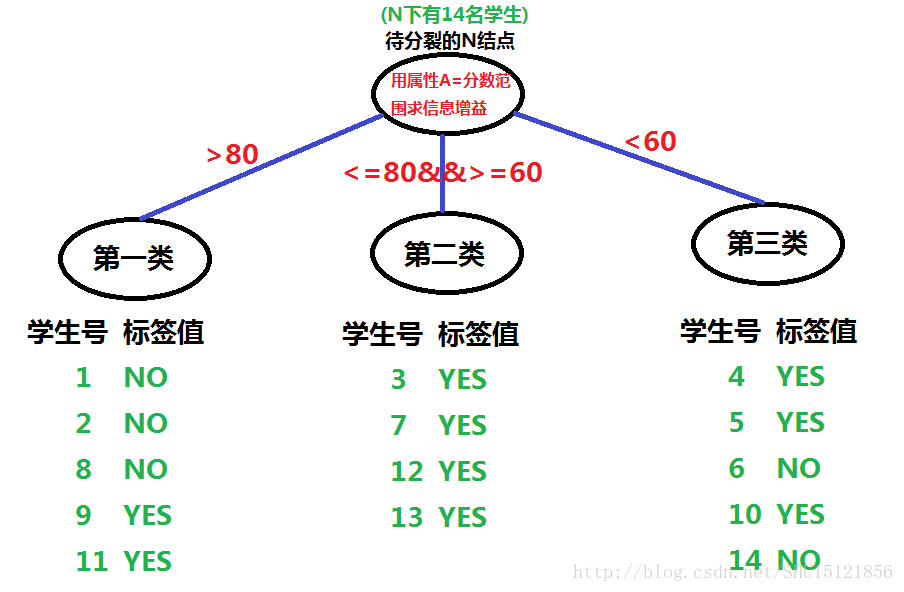
先计算结点N处的熵不纯度，这时和图中的具体分裂及属性没关系。只要看结点N下14个学生样本的标签值，一共有2类标签(YES和NO)，一共有9个YES，5个NO，所以N的熵不纯度：

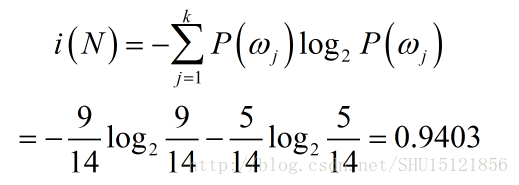
利用这个熵不纯度，再利用图上给出的每个类Nv占总体N的频率，以及每个类内样本标签YES/NO出现的情况(类内熵不纯度)，来计算用属性A=分数范围求得的A在N处的信息增量：

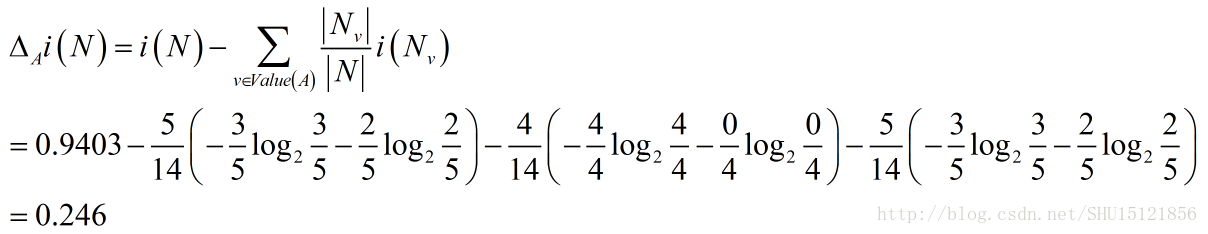
用同样的方式，再计算其它属性在N处的信息增量，选取最大的那个属性作为在结点N处的分裂方式。然后对结点N分裂，对新的节点把属性集合中去掉这个刚选取的属性，递归地去做，以构造整棵决策树。

ID3算法的递归有两种递归出口：如果结点下的样本标签值相同，则标记为该标签值然后返回；如果属性集合为空，则标记为该结点下最普遍出现的标签值然后返回。

C4.5算法

C4.5算法是对ID3算法的改进。因为ID3没有停止和剪枝技术，总是要把所有属性都用完，或者结点下标签已经完全相同才肯停止，这样很可能会overfitting。这里仅根据书上所述简单了解一下C4.5相比ID3额外做的事情。

分支停止

①验证：从训练集中拿出一部分做验证，直到决策树对验证集的分类误差最小为止。
②信息增益阈值：之前的ID3方式，每次向下分裂，信息增益是越来越小的，当最大信息增益小于我们设置的阈值时就干脆不分裂了，防止过学习：

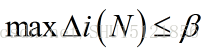
③全局目标最小化：为了兼顾叶节点熵不纯度(信息熵)较小和整个决策树复杂程度size不要太大这两件事，可以把它们按一定的权重α加起来，让这个和最小化作为全局目标：

④假设检验。还不理解，先记下来。

剪枝

对充分生长好后的决策树，虽然有了前面的分支停止做限制，仍然可能过于复杂，可以对这棵决策树再考虑剪枝问题。
①叶结点合并：如果挂在同一父结点上的两个叶节点合并后只引起很小(还是要给阈值)的熵不纯度(信息熵)增加，作合并。
②规则修剪：把生成的决策树根据每个结点的判别规则，转换成IF…THEN…形式的产生式规则，对每个叶子结点，用判别规则的合取和析取式来表示，对这样的规则集合找冗余，做修剪。这相当于是从离散数学的角度去化简逻辑公式，从而实现对决策树的剪枝。

最后

以上就是独特天空为你收集整理的【ML学习笔记】9：认识Decision Tree决策树的全部内容，希望文章能够帮你解决【ML学习笔记】9：认识Decision Tree决策树所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。