GBDT源码解读及实现（一）

GradientBoostingClassifier和GradientBoostingRegressor共同的父类是BaseGradientBoosting。BaseGradientBoosting的最重要的函数是fit()函数。fit()的开始是check_input、check_params等检查的功能。在check_params检查参数的时候初始化了损失函数self.loss_

def _validate_y(self, y):
    check_classification_targets(y)
    self.classes_, y = np.unique(y, return_inverse=True)
    self.n_classes_ = len(self.classes_)
    return y
    
def _check_params(self)：    
if self.loss == 'deviance':
            loss_class = (MultinomialDeviance
                          if len(self.classes_) > 2
                          else BinomialDeviance)
        else:
            loss_class = LOSS_FUNCTIONS[self.loss]

        if self.loss in ('huber', 'quantile'):
            self.loss_ = loss_class(self.n_classes_, self.alpha)
        else:
            self.loss_ = loss_class(self.n_classes_)

当loss='deviance’时len(self.classes_)=2所以 loss_class就是类BinomialDeviance,因此，self.loss_就是BinomialDeviance(2)。

接着判断是否初始化过（主要是区分是否是热启动的），如果没有初始化(我们主要看不是热启动的情况,下面代码中的if)

if not self._is_initialized():
   # init state
   self._init_state()

   # fit initial model - FIXME make sample_weight optional
   self.init_.fit(X, y, sample_weight)

   # init predictions
   y_pred = self.init_.predict(X)
   begin_at_stage = 0

初始化的时候，主要初始化最开始的模型，在_init_state()创建初始模型用的estimator

def _init_state(self):
     """Initialize model state and allocate model state data structures. """

     if self.init is None:
         self.init_ = self.loss_.init_estimator()
     elif isinstance(self.init, six.string_types):
         self.init_ = INIT_ESTIMATORS[self.init]()
     else:
         self.init_ = self.init

因此self.init_就是BinomialDeviance(2).init_estimator()

def init_estimator(self):
    return LogOddsEstimator()

class LogOddsEstimator(BaseEstimator):
    """An estimator predicting the log odds ratio."""
    scale = 1.0

    def fit(self, X, y, sample_weight=None):
        # pre-cond: pos, neg are encoded as 1, 0
        if sample_weight is None:
            pos = np.sum(y)
            neg = y.shape[0] - pos
        else:
            pos = np.sum(sample_weight * y)
            neg = np.sum(sample_weight * (1 - y))

        if neg == 0 or pos == 0:
            raise ValueError('y contains non binary labels.')
        self.prior = self.scale * np.log(pos / neg)

    def predict(self, X):
        check_is_fitted(self, 'prior')

        y = np.empty((X.shape[0], 1), dtype=np.float64)
        y.fill(self.prior)
        return y

因此初始化的y_pred就是LogOddsEstimator.predict(X)

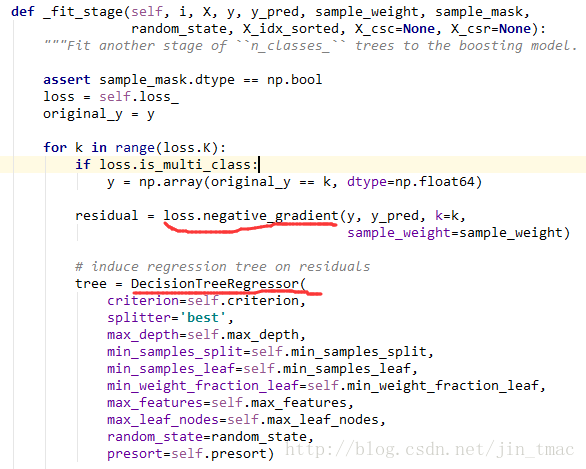
然后是在_fit_stages()函数里构建boosting的过程。
_fit_stages()中最重要的是迭代的更新每一个基础的learner。

其中_fit_stage是每一次的迭代，创建一棵决策回归树进行学习的过程。

The expit function, also
known as the logistic function, is defined as expit(x) = 1/(1+exp(-x)). It is the inverse of the logit function.

总结：
1、每棵树最开始的时候用残差作为预测值，第一棵树的残差是y_test-cnt(positive)/cnt(total)
2、对于二元分类，y_test就是0/1，残差就是y_test - y_pred，其中y_pred是概率值，类似于逻辑回归函数logit(p/1-p)=a+b1*X+…
中的P

3、第一步的pred是log(pos/neg)，残差residual就是y_test - 1/(1+exp(-pred))=y_test - pos/(pos+neg)
然后用X_test和residual进入回归树，
第二个回归树用的残差是y_test - logit(y_pred)(学习过)，但是不用回归树的value，而是logit(value(=from last_tree_region)*learning_rate+y_pred)

4、采用平方误差损失函数，$L(y,f(x))=(y-f(x){)}^2$
其损失变为 $L(y,f_{m-1}(x)+T(x;{\Theta }_m))$
$=[y-f_{m-1}(x)-T(x;{\Theta }_m)){]}^2$
$=[r-T(x;{\Theta }_m)){]}^2$
这里，$r=y-f_{m-1(x)}$是当前模型拟合数据的残差(residual)。
在GBDT中，$f(x)=1/(1+exp(-x))$

最后

以上就是想人陪高山为你收集整理的GBDT源码解读及实现（一）的全部内容，希望文章能够帮你解决GBDT源码解读及实现（一）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。