动态规划(Dynamic Programming, DP)思想启发于分治算法的思想,也是将复杂问题化解若干子问题,先求解小问题,再根据小问题的解得到原问题的解。但是DP与分治算法不同的是,DP分解的若干子问题,往往是互相不独立的,这时如果用分治算法求解,那么会对重叠子问题重复进行求解,从而使得浪费大量的时间。那么如果我们保存已经计算过的子问题的解,这样当再次计算该子问题时,可以直接使用,这样可以节约大量的时间。
DP正是利用一个表记录所有已经求解过的子问题的答案,只要一个子问题被求解过,就将其答案保存起来,无论以后的计算是否会用到,这就是DP的基本思想。
设计动态规划的四个步骤:
1、刻画一个最优解的结构特征。
2、递归地定义最优解的值。
3、计算最优解的值,通常采用自底向上的方法。
4、利用计算出的信息构造一个最优解。
动态规划的应具备两个要素:
1、最优子结构性质。当问题的最优解包含了其子问题的最优解时,称该问题具有最有子结构性质;
2、重叠子问题性质。
首先看一个算法导论中第一个例子,钢条切割问题。
问题:给定一根长度为n英寸的钢条和一个价格表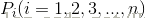 ,求钢条的最佳切割方案,使得销售收益
,求钢条的最佳切割方案,使得销售收益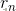 最大。
最大。

对于长度为n的钢条总共有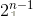 种不同的切割方案。设距离钢条左端i(i = 1,2,....n-1)英寸处为可切割点,那么我们对每个切割点都可以选择切或者不切,则总共有
种不同的切割方案。设距离钢条左端i(i = 1,2,....n-1)英寸处为可切割点,那么我们对每个切割点都可以选择切或者不切,则总共有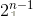 种方法。因此暴力枚举每一种可能是不行的。
种方法。因此暴力枚举每一种可能是不行的。
设长度为n的钢条的最大收益为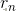 (n>=1)。
(n>=1)。
1、最优子结构
对于长度为n的钢条,假设第一刀在i(i= 1,.....n-1)处切割,使得收益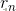 最大。得到的两个小段钢条长度为i,n-i,那么对于其收益
最大。得到的两个小段钢条长度为i,n-i,那么对于其收益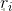 和
和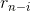 也是最大的。假设不是,即在长度为i和长度为n-i的钢条分别有更好的切割方案,使得对应的收益更大,那么将这两个更优切割方案的收益相加,会得到一个比在i处切割所得收益更大的方案,那么说明开始第一刀就不是最优的,与假设相矛盾!因此本问题具有最有子结构的性质。
也是最大的。假设不是,即在长度为i和长度为n-i的钢条分别有更好的切割方案,使得对应的收益更大,那么将这两个更优切割方案的收益相加,会得到一个比在i处切割所得收益更大的方案,那么说明开始第一刀就不是最优的,与假设相矛盾!因此本问题具有最有子结构的性质。
2、递归地定义最优解的值
有一个更加简单明了的切割方法,假设我们最优的第一刀直接切出一个距离左端为i(i = 1, ....n-1)的钢条,这一段整体收益最大,即不再对这一段继续切割。我们只对剩余长度为n-i的钢条,继续切割,求其收益最大的切割方案,这样问题只化为一个更小的子问题。
由此,我们可以知道长度为n的递推公式为:
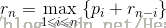
若i取n时表示整体不切割,收益最大,此时剩余部分n-i的收益为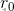 为0。
为0。
3、计算最优解的值
我们先根据2的递推公式,用递归的方式先求解,如下:
int CutRod(int p[], int n)
{
if(n == 0)
return 0;
int q = INT_MIN;
for(int i = 1; i <= n; ++i)
if(q < p[i]+CutRod(p, n-i))
q = p[i]+CutRod(p, n-i);
return q;
} 开始的时候,我们说过,对于切割点i(i = 1, ...., n-1),我们可以选择切或者不切,总共有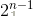 种情况,由此我们可以知道该算法的时间复杂度为
种情况,由此我们可以知道该算法的时间复杂度为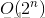 ,(其实它枚举了每一种情况),这是一个指数级的算法,肯定是不行的。那么时间浪费在哪里了?
,(其实它枚举了每一种情况),这是一个指数级的算法,肯定是不行的。那么时间浪费在哪里了?
我们用当n=4时,做个例子,其递归过程如下:
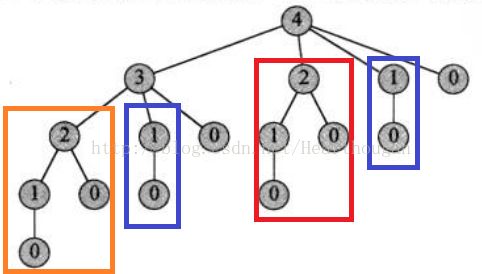
每个节点表示子问题的规模,从父节点s到子节点t的边,表示从钢条的左端切下一段长度为s-t的小钢条,然后递归地求解剩余规模为t的子问题。
由上图可以知道,有很多相同的子问题,被大量的重复计算,从而浪费了大量的时间,那么如何解决这问题?我们可以用空间来换取时间,申请一张表,来储存每次新子问题的答案,这样下次再遇到相同的子问题,直接查表取得,而无需计算,从而可以节约大量的时间。
int CutRod(int p[], int r[], int n)
{
if(r[n] >= 0)
return r[n];
if(n == 0)
return 0;
int q = INT_MIN;
for(int i = 1; i <= n; ++i)
if(q < p[i]+CutRod(p, r, n-i))
q = p[i]+CutRod(p, r, n-i);
r[n] = q;
return q;
}
int MemoizedCutRod(int p[], int n)
{
int r[n+1];
for(int i = 0; i <= n; ++i)
r[i] = INT_MIN;
return
} 这是一个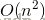 的算法,由此可以看出,算法的效率得到了大大的提高。
的算法,由此可以看出,算法的效率得到了大大的提高。
我们知道,每次递归调用函数,这也是需要时间花销的,我们上面的算法实现全部都是用自上而下的思想来求解最优值的,由1,我们知道子问题的最优解决定着原问题的最优解,那么可以从最小规模开始计算,这样当计算规模较大的问题时,所需的子问题已经全部计算出来,并且被记录下来,这样就可以直接拿来使用,这就自底向上的思想来求解最优值,该问题的自底向上方法的实现如下:
#include <iostream>
#include <cstdlib>
#include <cstring>
using namespace std;
int main()
{
int n;
cin>>n;
int price[11] = {0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30};
int r[n+1];
for(int i = 0; i<= n; ++i)
r[i] = 0;
for(int i = 1; i <= n; ++i)//规模长度为i
{
int q = INT_MIN;
for(int j = 1; j <= i; ++j)//计算规模为i的最大收益
{
if(q < price[j] + r[i-j])//因为i>i-j,所以当计算r[i]时,r[i-j]已经解决,可以直接用
q = price[j] + r[i-j];
}
r[i] = q;
}
cout<<r[n];
}4、利用计算出的信息构造一个最优解
如果只需求解最大收益,这么此步可以被省略,但是如果需要打印出来最佳的切割方案,那么原算法仍需稍微改动。我们另外申请一个数组label[],专门来存储最佳切割点的。其实现如下:
#include <iostream>
#include <cstdlib>
#include <cstring>
using namespace std;
int main()
{
int n;
cin>>n;
int price[11] = {0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30};
int r[n+1];
int label[n+1];
memset(label, 0, sizeof(label));
for(int i = 0; i<= n; ++i)
r[i] = 0;
for(int i = 1; i <= n; ++i)//规模长度为i
{
int q = INT_MIN;
for(int j = 1; j <= i; ++j)//计算规模为i的最大收益
{
if(q < price[j] + r[i-j])//因为i>i-j,所以当计算r[i]时,r[i-j]已经解决,可以直接用
{
q = price[j] + r[i-j];
label[i] = j;
}
}
r[i] = q;
}
cout<<r[n]<<endl;
//打印最佳切割方案
while(n > 0)
{
cout<<label[n]<<" ";
n = n - label[n];
}
cout<<endl;
}那么到此,我们利用DP的设计步骤全部实现钢条的切割问题,下面我们再看一个矩阵相乘的例子,这是把原问题分解为两个子问题,来求解矩阵相乘所需的最小次数的。请参考本人笔记:
http://blog.csdn.net/hearthougan/article/details/25834141
由这两个问题我们可以更加深刻地理解DP的两个要素。何时需要动态规划,主要也是考察问题是否具备这两个要素,现在分析一下这两个要素:
I、最优子结构
这是动态规划求解最优解的第一步。最优子结构性质是:一个问题的最优解包含其子问题的最优解。发掘最优子结构性质的过程,遵循如下模式:
1、证明问题最优解的第一个组成部分是做出一个选择。如,选择钢条第一次切割的位置,第一次选择矩阵链的划分位置等。做出这次选择会产生一个或者多个待解的子问题。
2、对于一个给定问题,在其可能的第一步选择中,你假,定已经知道哪种选择才会得到最优解。现在无需关心这种选择是如何得到的,只是假定已经知道了这种选择。
3、给定可获得最优解选择后,确定这次选择会产生哪些子问题,以及如何更好地刻画子空间。一个刻画子问题空间的经验是:保持子问题空间尽可能简单,只在必要时才扩展它。
4、利用Cut-and-paste方法证明:作为原问题最优解的组成部分,每个子问题的解就是它本身的最优解。证明这一点,就是利用反证法:假定子问题的解不是其自身的最优解,那么我们可以从原问题中“剪切”掉这些非最优解,将最优解“粘贴”进去,从而得到一个原问题更优的解,这与最初的解释原问题的最优解的前提假设相矛盾。
对于不同的问题,最优子结构体现在两个方面:
1、原问题的最优解涉及多少个子问题
2、在确定最优解使用哪些子问题时,我们需要考察多少种选择。
II、重叠子问题
适合动态规划方法求解最优解的问题应该具备:子问题的空间必须足够“小”,即问题的递归算法会反复地求解相同的子问题,而不是一直生成新的子问题。重叠子问题性质:递归算法反复求解相同的子问题。
与之对应的分治算法,其求解问题时,通常在递归的每一步都生成全新的子问题。而动态规划则是,把子问题的解存放在一张表里,在需要的时候直接取出,此步操作的时间复杂仅是常量时间,故而降低了时间复杂度!
最后
以上就是欣慰学姐最近收集整理的关于动态规划总结的全部内容,更多相关动态规划总结内容请搜索靠谱客的其他文章。








发表评论 取消回复