动态规划阶段性总结3 2021.7.27

一、初值条件确定方法：

以二维DP为例，通常有3种确定方式：
(设两维的范围分别为[0,m]  [0,n])
1.设置dp[0][0…n]
2.设置dp[0…m][0]
3.设置dp[0][0]
具体如何设置，应根据题意而定。如果发现其中一种不行，可改变为另一种。如果实在无法确定，可按照3->2->1->(1+2)的顺序依次尝试。

  对于计数问题，如果状态转移方程中没有 +（常数），那么初始值应当设置为1，否则可以设置为0。
  对于最大/最小值问题，将初值设置为0（或-INF）/INF。
动态规划问题，特别是与背包相关的动态规划，常常考虑“选”与“不选”两种情况。
例：

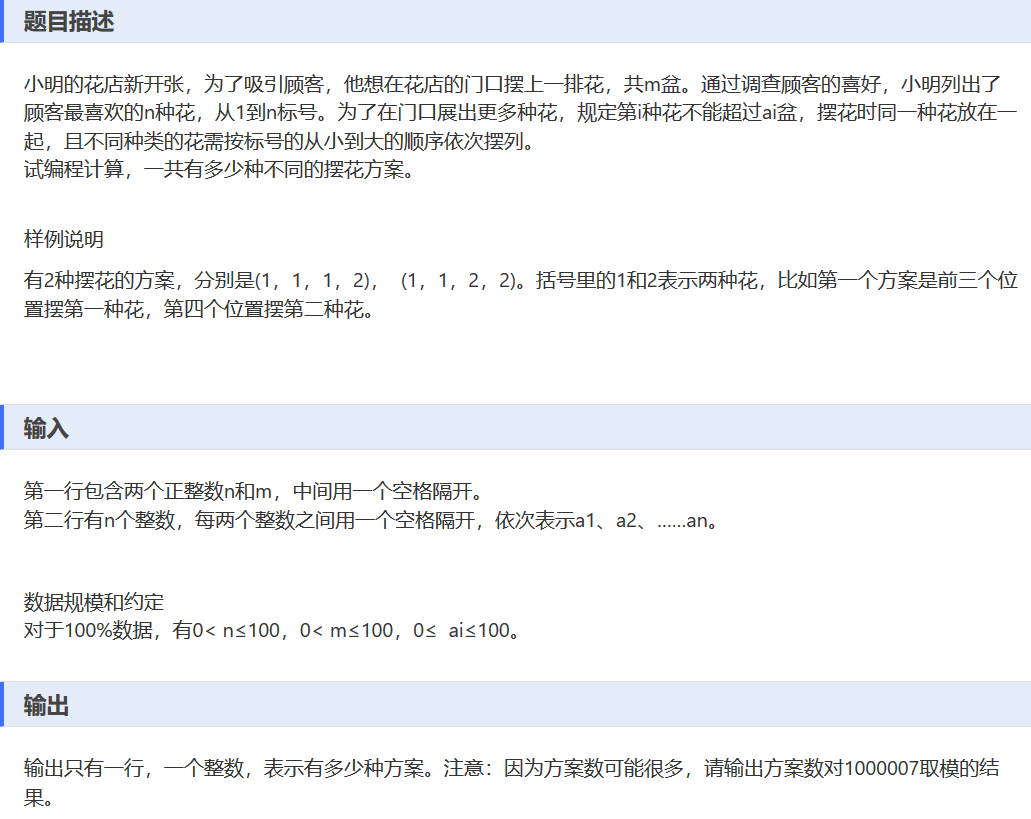
我在做这题时发现，虽然样例能通过，但其中部分dp的值不正确，经检查状态转移方程没错，就是初值条件中少设一个dp[0][0]=1（第一维代表位置，第二维代表花的编号）或者认为只需要另dp[0][0]=1，其实把两个结合起来就行了。

二、测试程序的方法

鉴于动态规划的特性，不能以为最后结果对程序就没问题，过程中所有值都必须正确。可以借助手动分析列表，再断点调试查看数组中每个值与表中是否相等。也可写一个暴力搜索程序与之对比，甚至可以打表 。

1.如果能看出是背包，那么可以直接用一维。
2.如果想对数组按奇偶性进行优化，一定要注意先初始化，比如本题：dp[i&1][j]=(dp[i&1][j]+dp[(i-1)&1][j-k])%MOD; 因为dp[i][j]要利用自身进行更新，因此二三层循环间要加一句dp[i&1][j]=0

最后

以上就是难过金鱼为你收集整理的动态规划阶段性总结3 2021.7.27的全部内容，希望文章能够帮你解决动态规划阶段性总结3 2021.7.27所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。