D. Unusual Sequences (数论,质因子分解,dp)

81 阅读 0 评论 54 点赞

我是靠谱客的博主搞怪保温杯，最近开发中收集的这篇文章主要介绍D. Unusual Sequences (数论,质因子分解,dp)，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

Count the number of distinct sequences a1, a2, ..., an (1 ≤ ai) consisting of positive integers such that gcd(a1, a2, ..., an) = x and 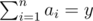$\text{[math]}$ . As this number could be large, print the answer modulo 109 + 7.

gcd here means the greatest common divisor.

Input

The only line contains two positive integers x and y (1 ≤ x, y ≤ 109).

Output

Print the number of such sequences modulo 109 + 7.

   Examples 
 
     input 
    
      Copy 
    
3 9

     output 
    
      Copy 
    
3

     input 
    
      Copy 
    
5 8

     output 
    
      Copy 
    
0

Note

There are three suitable sequences in the first test: (3, 3, 3), (3, 6), (6, 3).

There are no suitable sequences in the second test.

题意:构造数列使得gcd(a1,a2,...,an)=n && a1+a2+...+an=m 询问共有多少种构造方法。

题解:首先可知m%n必须为0,否则无法构造,此时可分出m/n个n,利用隔板法可得共有qpow(2,m/n-1)种方案,然后再将 gcd==k*n 的方案减去即可。

#include<stdio.h>
#include<algorithm>
#include<iostream>
#include<string.h>
#include<vector>
#include<stdlib.h>
#include<math.h>
#include<queue>
#include<deque>
#include<ctype.h>
#include<map>
#include<set>
#include<stack>
#include<string>
#include<algorithm>
#define gcd(a,b) __gcd(a,b)
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define FAST_IO ios::sync_with_stdio(false)
#define mem(a,b) memset(a,b,sizeof(a))
const double PI = acos(-1.0);
const double eps = 1e-6;
const int MAX=1e6+10;
const long long INF=0x7FFFFFFFFFFFFFFFLL;
const int inf=0x3f3f3f3f;
typedef long long ll;
using namespace std;
const int mod=1e9+7;

ll qpow(ll a,ll b)
{
    ll ans=1;
    while(b)
    {
        if(b&1)
            ans=(ans*a)%mod;
        a=(a*a)%mod;
        b/=2;
    }
    return ans;
}

ll dp[10005];
int main()
{
    ll n,m;
    while(cin>>n>>m)
    {
        vector<ll>v;
        if(m%n)
        {
            printf("0n");
            continue;
        }

        for(ll i=1;i<=sqrt(m);i++) //将m的因子中为n的倍数的数找出来
        {
            if(m%i==0)
            {
                if(i%n==0) v.push_back(i);
                if(i*i!=m && m/i%n==0) v.push_back(m/i);
            }
        }
        sort(v.begin(),v.end());

        for(int i=v.size()-1;i>=0;i--)
        {
            dp[i]=qpow(2,m/v[i]-1); //构造gcd为(i+1)*n的序列的总方案数
            for(int j=i+1;j<v.size();j++) //dp递推过去
                if(v[j]%v[i]==0)
                    dp[i]=(dp[i]-dp[j]+mod)%mod; //构造gcd为x的需要减去gcd为2*x,3*x....,所以倒着递推
        }

        printf("%I64dn",dp[0]);
    }
    return 0;
}