莫队

参考资料：https://www.cnblogs.com/WAMonster/p/10118934.html

更好的阅读体验

建议去上面cnblog查看，csdn公式挂了不少

前言——引入

关于莫队算法发明者——莫队·莫涛

众所周知，OIer常用“*队”来称呼实力强大的选手，就如：李队，刘队，杨队，何队 %%%%%

这位莫队，实在是太强了：

【NOI2009】 $577$ 全国Rk1 ；前国家队队长

OrzOrzOrzOrzOrzOrzOrzOrzOrzOrzOrzOrzOrzOrzOrzOrzOrzOrzOrzOrzOrzOrzOrzOrzOrzOrzOrzOrzOrzOrz

关于莫队算法

$$\{\begin{array}{l}普通莫队\\ 带修莫队\\ 树上莫队\\ 回滚莫队\end{array}$$

大致分为这4类莫队算法

*注：只有普通莫队是莫涛提出的，其余都是后人根据不同情况YY得出的。

（莫涛在论文中说了，其实CF上有很多大神都会用莫队算法，只不过没人统一提出）

万谔恶的区间问题

例如最基本的：RMQ，线段树，树状数组，分块……

随之时代的变迁，越来越多毒瘤出题人横空出世！

区间问题变得越来越难

像我一样的蒟蒻OIer渴求一种好写，相对速度较快的数据结构

这时，莫队算法的出现，给蒟蒻们带来了一丝曙光……

莫队算法——优雅而不失复杂度的暴力

像暴力一样好写，又有分块一样时间复杂度，常数还小（不过要离线

如果从$[l,r]$ 的答案能够 $O(1)$扩展到 $[l+1,r][l-1,r][l,r+1][l,r-1]$（即与$[l,r]$相邻的区间）的答案，那么使用莫队算法可以在$O(n\sqrt{n})$的复杂度内求出所有询问的答案。

莫队算法基本原理

双指针跳跃

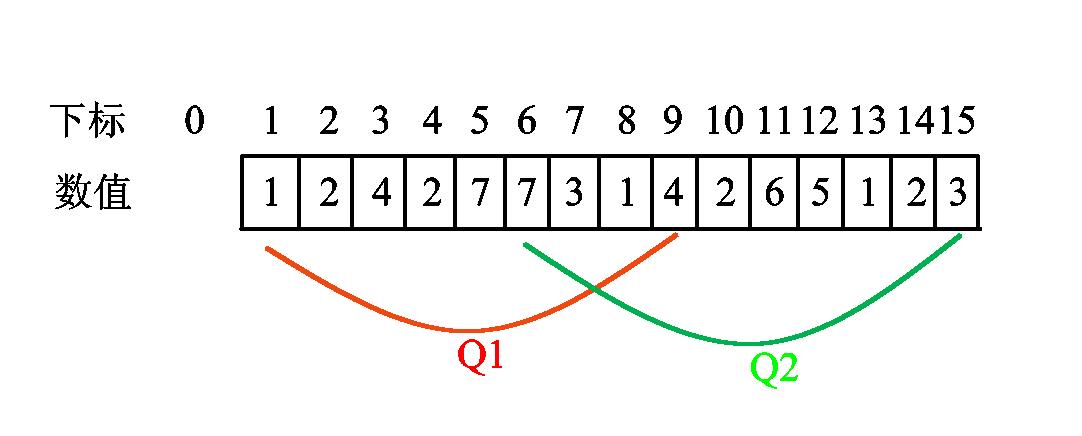
如上图，假如我们要求$Q2$的区间和，并且我们知道了$Q1$的区间和

1.我们可以把$Q1$的右指针右移，沿路加上经过数值的值，这样我们就算出了区间$[1,15]$的区间和

2.然后我们将$Q1$的左指针右移，沿路减去经过数值的值，这样我们就算出了区间$[6,15]$的区间和

同理，从$Q2$到$Q1$也是如此（右移变左移），非常简单，不提了。

我们将$1$操作成为加入操作，$2$操作称为删除操作

莫队中的加入和删除操作是解决问题的核心。

上面的例题未免太简单了，来看看正常一点的题P3901 数列找不同

先不考虑时间复杂度，用双指针跳跃如何做此题

思考ing……

	1	2	3	4
a	1	2	3	2
1	**		**
2		**		**

假设我们当前在$[l,r]$区间

我们用$vis[i]$表示当前区间中数字$i$出现的次数，

那么假如有某个$i$的$vis[i]$超过了$1$，那么代表当前区间不是互不相同的

再用一个$sum$计数器，表示当前区间中$vis[i]$超过$1$的$i$的个数

如果$sum$不是$0$，那么代表当前区间不是互不相同的

我们的加入操作怎么写？每加入一个数$i$，$vis[i]$数组加$1$，如果$vis[i]$由$1$变为超过$1$,那么$sum+1$

删除同理，每删除一个数，$vis[i]$数组减$1$，如果$vis[i]$从超过$1$变为$1$，那么$sum-1$

移动到指定区间后，判断$sum$的值，如果$sum$大于0则$No$，否则输出$Yes$.

核心代码：

void add(int x){if(vis[v[x]]==1)ans++;vis[v[x]]++;}	//加入操作
void remove(int x){vis[v[x]]--;if(vis[v[x]]==1)ans--;}//删除操作

	l=1;r=0;
	for(int i=1;i<=m;i++){
		while(l>a[i].l)add(--l);//左指针往左移加入
		while(l<a[i].l)remove(l++);//左指针往右移删除
		while(r<a[i].r)add(++r);//右指针往右移加入
		while(r>a[i].r)remove(r--);//右指针往左移删除
		if(ans==0)a[i].ans=0;		//Yes
		else a[i].ans=1;			//No
	}

既然上了代码，我来讲讲莫队中要注意的细节——指针移动

首先可以明确一点：

左指针向左移是加入操作，向右移是删除操作

右指针向左移是删除操作，向右移是加入操作

易证，自己可以画图领悟

然后，我们要明白，加入操作是先移动指针，再将指向的值加入

而删除是先将指针所指的值删除，再将指针移动

这个细节很重要，要想清楚再写代码

还有就是刚开始的区间是$[1,0]$，可以发现很奇怪啊

不应该$l<=r$吗，怎么$l>r$了

我们可以用前缀和的思想想一下

$l$代表什么？代表$[0,l)$的位置都删除过了

$r$代表什么？代表$[0,r]$的位置都加入过了

那么代入$l=1,r=0$正好就是区间$[0,0]$，也就是什么都没有。

那就可以解释得通了！

重中之重——莫队

前面是基础，后面才是莫队

明显，如果我们按询问区间这样暴力去跳左右指针，是可以被卡成$O(n^2)$的

例如下图：

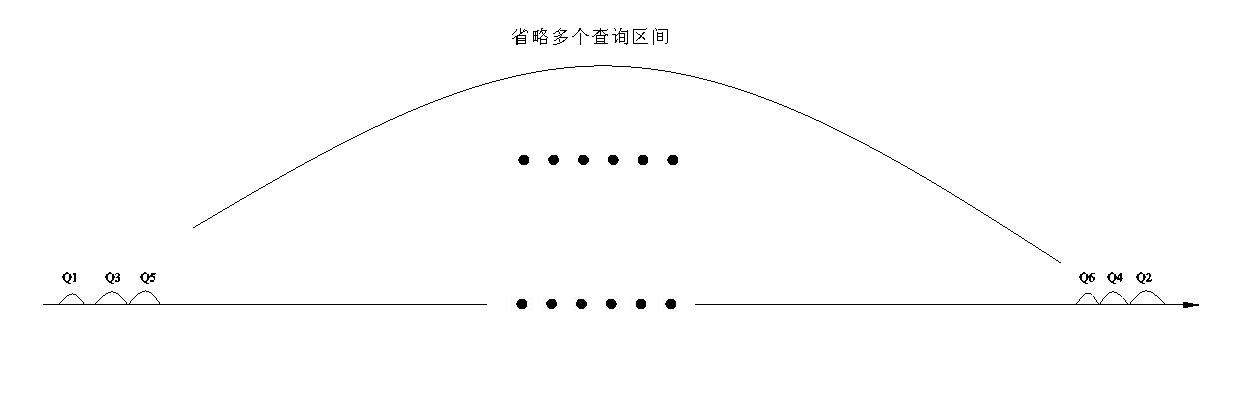
这就十分不爽了，我们要快一点！

莫队算法便是将上面的方法优化到了$O(n\sqrt{n})$

我们想重新安排一下询问的顺序，使总体的指针跳跃量尽可能地小

算法流程：

我们将长度为$n$的序列分成$O(\sqrt{n})$块，从$1$至$\sqrt{n}$编号。

然后标记每一个点所属的块$block[i]$ (表示$i$点属于块的编号)

然后我们对询问排序：

先按左端点所在的块编号为第一关键字排序

如果相同，则按右端点的位置排序

然后按排序后的顺序处理每一个询问，求得答案

再通过一次排序复原原来的顺序。

贴代码：

bool cmp1(kkk a,kkk b){return a.id<b.id;}		//复原原来顺序
bool cmp(kkk a,kkk b){							//询问排序
	if(blo[a.l]!=blo[b.l])return a.l<b.l;		//先按左端点所在块为第一关键字排序
	else return a.r<b.r;						//相同则按右端点排序
}
……
block=sqrt(n);	//块大小
for(int i=1;i<=n;i++)blo[i]=(i-1)/block+1;		//划分块
for(int i=1;i<=m;i++){
    scanf("%lld%lld",&a[i].l,&a[i].r);
    a[i].id=i;	//标记原来编号
}
sort(a+1,a+m+1,cmp);	//对询问排序
……
sort(a+1,a+m+1,cmp1);	//复原顺序

WOW，好短，绝对是数据结构在代码短层面上一流的！

复杂度分析：

？就这？这样就可以把复杂度降低很多？

嗯~，没错，这样就可以将时间复杂度降低到$O(n\sqrt{n})$

时间复杂度分为：

1.排序 $O(nlogn)$

2.设每个块$i$中分布有$x_i$个左端点，那么处理块$i$的最坏时间复杂度是$O(x_i\sqrt{n})$，指针跨越整个块的时间复杂度是$O(\sqrt{n})$ ,要跨越$\sqrt{n}$次，所以总复杂度约为$O(\sum x_i\sqrt{n}+\sqrt{n}\sqrt{n})=O(n\sqrt{n}+n)$

3.右端点在一个左端点相同的块内是有序的，那么对于每一个块$i$中的$x_i$个区间，右端点最多跳完整一个序列（就是不会往回跳），一共有$\sqrt{n}$个块，所以总复杂度为$O(n\sqrt{n})$

至此，莫队算法的时间复杂度约为$O(n\sqrt{n})$

上面是我搞懂的一个证明，下面是大佬的证明，可以看看：

• 分块相同时，右端点递增是的，分块共有个，复杂度为
• 分块转移时，右端点最多变化，分块共有个，复杂度为
• 分块相同时，左端点最多变化，分块转移时，左端点最多变化，共有个询问，复杂度为

莫队的优化

奇偶优化

对于左端点在同一奇数(编号)块时，右端点按升序排序，在同一偶数(编号)块时，右端点按降序排序。

bool cmp(kkk a,kkk b){
	if(blo[a.l]!=blo[b.l])return a.l<b.l;
	if(blo[a.l]%2==0)return a.r>b.r;//多加了行判断
	return a.r<b.r;
}

调节块大小

据数据结构神lxl大佬说，普通莫队将块大小调节成$\frac{n}{\sqrt{m}}$ 会块。

block=n/sqrt(m);

%%%lxl

来证明一下：

设每一块的大小为$T$，序列长为$n$，询问个数为$m$.

那么最多有$n/T$块。

对于右端点的移动，每一块最多移动$n$次，有$n/T$块，所以右端点时间复杂度为$O(n^2/T)$

对于左端点的移动，每一次最多移动$T$次，有$m$次移动，所以左端点时间复杂度为$O(mT)$

那么总时间复杂度为$O(n^2/T+mT)$

设$n^2/T+mT=S$

原式等于 $n^2+m{T}^2-ST=0$

这样变为一个经典的二次函数求最小值的问题

$Delta=S^2-4mn2>=0 $

为取到最小值，$\Delta =0$

那么$S^2-4m{n}^2=0$

$S^2=4m{n}^2$

$S=2\sqrt{m}n$

代入回$x=\frac{-b+\sqrt{\Delta }}{2a}$

算出$T=\frac{n}{\sqrt{m}}$

Q.E.D

---

那么看到现在，相信大家都已经掌握了普通莫队了吧

让我们来练几道简单的例题！

例题

P1494[国家集训队]小Z的袜子

题意：给出一个N个数的序列，M个询问，每次询问区间$[l,r]$中随机挑出$2$个数，这两个数相等的概率是多少？用最简分数表示，即输出x/y的格式

莫队的模板大家都会打，我们要思考的问题是加入和删除操作而已

假设此时有$x$对颜色为$a$的袜子，那么取到一对$a$的方案数是$a(a-1)$ 很显然吧

那么加入$1$只颜色为$a$的袜子，我们把原来取一对颜色$a$的方案数减掉，然后更新$a$的数量

再把取一对颜色$a$的方案数加回去

删除反之依然同理

答案即为$(总方案数/(区间长度\ast (区间长度-1)))$

额，不知道为什么题解有人化式子……暴力不香吗

#include<bits/stdc++.h>
#define maxn 100001
using namespace std;
struct kkk{
	long long l,r,id,a,b;
}a[maxn];
long long ans,ansl[maxn],ansr[maxn],gcd;
int blo[maxn],block,n,m,l,r,tag[maxn],v[maxn];
bool cmp1(kkk a,kkk b){return a.id<b.id;}
bool cmp(kkk a,kkk b){
	if(blo[a.l]!=blo[b.l])return a.l<b.l;
	if(blo[a.l]%2==0)return a.r>b.r;//多加了行判断
	return a.r<b.r;
}
void add(int x){ans-=tag[v[x]]*(tag[v[x]]-1);tag[v[x]]++;ans+=tag[v[x]]*(tag[v[x]]-1);}
void remove(int x){ans-=tag[v[x]]*(tag[v[x]]-1);tag[v[x]]--;ans+=tag[v[x]]*(tag[v[x]]-1);}
int main(){
	scanf("%d%d",&n,&m);block=n/sqrt(m);
	for(int i=1;i<=n;i++)scanf("%d",&v[i]);
	for(int i=1;i<=n;i++)blo[i]=(i-1)/block+1;
	for(int i=1;i<=m;i++){
		scanf("%d%d",&a[i].l,&a[i].r);
		a[i].id=i;
	}
	sort(a+1,a+m+1,cmp);
	l=1;r=0;
	for(int i=1;i<=m;i++){
		while(l>a[i].l)add(--l);
		while(l<a[i].l)remove(l++);
		while(r<a[i].r)add(++r);
		while(r>a[i].r)remove(r--);
		if(a[i].l==a[i].r){
			ansl[i]=0;ansr[i]=1;
			a[i].a=ansl[i];a[i].b=ansr[i];
			continue;
		}
		ansl[i]=ans;
		ansr[i]=(a[i].r-a[i].l+1)*(a[i].r-a[i].l);
		gcd=__gcd(ansl[i],ansr[i]);
		ansl[i]/=gcd;ansr[i]/=gcd;
		a[i].a=ansl[i];a[i].b=ansr[i];
		//printf("%dn",ansr[i]);
	}
	sort(a+1,a+m+1,cmp1);
	for(int i=1;i<=m;i++)
	printf("%lld/%lldn",a[i].a,a[i].b);
}

小B的询问

题意：给出一个长度为$n$的序列，$m$个询问，每次求区间$[l,r]$中(每个数字出现次数的平方)的和

这…… 好水，板子题

对于加入一个数字$i$，先把它原来的贡献减去，更新出现次数，再加上新的贡献

删除同理。搞定了

P3709 大爷的字符串题

首先你可能看1h也看不懂题意……

所以看这里：

给你$n$个数,$m$次询问区间$[l,r]$中众数的出现次数

记录一个数组$vis[i]$表示$i$出现次数，$cnt[i]$表示出现次数为$i$的数有多少个？

当我们加入一个数，更新两个数组，$ans$为$max(ans,cnt[i])$

删除就有点麻烦，如果数$i$是众数，并且是唯一一个众数，那么$ans$要减$1$

否则直接更新数组即可。

[CQOI2018]异或序列

题意：给出一个长度为$n$的序列和一个正整数$k$，$m$个询问，每次询问区间$[l,r]$中有多少个连续的子序列的异或和为$k$ .

给点时间想想吧

如果你熟悉异或的一些性质，那这题应该对你不难

我们知道 区间$[l,r]$的异或和$=$$[1,r]\wedge [1,l-1]$

那我们先预处理出前缀异或和$a[i]$

我们还知道 如果$x\wedge y=k$ 那么 $x\wedge k=y$

对于加入一个数$x$，能和$x$产生贡献的就是$[l,r]$中前缀异或和$y$能满足$x\wedge y=k$的数

那么我们只需要知道$[l,r]$中前缀异或和是$x\wedge k$ 的数有多少就好了

用莫队维护$[l,r]$中前缀异或和的桶$vis$，每次加入答案加上KaTeX parse error: Undefined control sequence: and at position 6: vis[x̲a̲n̲d̲ ̲k] 即可

void add(int x){ans+=vis[a[x]^k];vis[a[x]]++;}
void del(int x){vis[a[x]]--;ans-=vis[a[x]^k];}

注意加减和更新答案的顺序

---

那么看到这里，你已经学会了最基础的莫队了！

恭喜！

现在我们来进阶……

莫队套分块

当两个根号算法通过某种不知名手段交融在一起时，会产生一些奇怪的题目……

前置知识：值域分块+莫队

如果你不会分块，那依然可以继续看下去，毕竟分块比较好理解

先来看一道题 [AHOI2013]作业

题意：给出一个长度为$N$的序列，$M$个询问，每个询问给出$l,r,a,b$，表示查询区间$[l,r]$中有多少个数在值域$[a,b]$中和区间$[l,r]$中有多少种数字在值域$[a,b]$中。

也就是对于每个询问需回答两个答案：

区间$[l,r]$中值域$[a,b]$的数的个数，重复算

区间$[l,r]$中值域$[a,b]$的数的个数，重复不算

这个最好先思考一下，看看自己有什么想法

此题树套树，cdq分治都可过

不过代码嘛……肯定没有莫队辣么好写啦！

通过前面的学习，我们可以轻易算出区间$[l,r]$中不同的数的个数。

但题目有一个值域的限制，也就是我们无法在移动值域指针的同时计算出答案了。

那我们把问题简化，移动左右指针视为值域上单点修改，最后统一值域区间查询。

大部分人都会想到树状数组。

不过树状数组单点修改带一个$log$，会给复杂度多乘一个$log$，这可不行

那有什么单点修改$O(1)$，并且区间查询不慢的算法呢？

值域分块！

考虑一下莫队的本质，即莫队的复杂度分析，本质上分析的是 $l,r$ 移动的复杂度，也就是修改的复杂度。所以莫队可以本质上看成一个 $O(n\sqrt{m})$ 修改，$O(m)$询问的数据结构。观察到询问数较少，于是可以用一个可以快速修改，低速查询的 数据结构 来维护值域，那这自然就是值域分块，最终复杂度 $O(n\sqrt{m}+m\sqrt{n})$。

我们把数的值域分为$\sqrt{maxn}$块，每一块代表对应值域，如第一块为$[1,\sqrt{maxn}]$ 第二块为$[\sqrt{maxn}+1,2\ast \sqrt{maxn}]$ 。莫队的增加和修改操作就是在值域上增加和删除。这时，我们维护值域块内的数的个数$sum$。

查询时我们先对散块进行处理，再对整块进行处理。单次查询时间复杂度$O(\sqrt{maxn})$

考虑到这题值域很小，可以过

同理第二个问题用相同思路维护

$num[i]$表示值$i$的个数，$sum[i]$表示块一共有多少个数，$vis[i]$表示是否有值$i$这个数，$sum1[i]$表示块一共有多少种数

贴代码理解吧

#include<bits/stdc++.h>
#define maxn 1000001
using namespace std;
int block,blo[maxn],bl[maxn],br[maxn],blocknum,bloc[maxn];
int n,m,vis[maxn],ANS[maxn],a[maxn],ANS2[maxn],sum1[maxn];
int num[maxn],sum[maxn],res,B,maxx;
struct kkk{
	int l,r,a,b,id;
}q[maxn];
bool cmp1(const kkk &a,const kkk &b){
	if(blo[a.l]!=blo[b.l])return a.l<b.l;
	if(blo[a.l]%2==1)return a.r<b.r;
	return a.r>b.r;
}
void modify(int x,int val){
	num[x]+=val;sum[bloc[x]]+=val;		//第一个问题值更新
	if(num[x]==1&&val==1)vis[x]=1,sum1[bloc[x]]++;	//第二问对于加值
	if(num[x]==0&&val==-1)vis[x]=0,sum1[bloc[x]]--;	//第二问对于删值
}
int query(int a,int b){
	if(a>b)return 0;	//特判
	int ans=0;
	if(bloc[a]==bloc[b]){for(int i=a;i<=b;i++)ans+=num[i];return ans;}	//在相同块特殊处理
	for(int i=a;i<=br[bloc[a]];i++)ans+=num[i];	//左散块处理
	for(int i=bl[bloc[b]];i<=b;i++)ans+=num[i];	//右散块处理
	for(int i=bloc[a]+1;i<=bloc[b]-1;i++)ans+=sum[i];	//整块处理
	return ans;
}
int query2(int a,int b){
	if(a>b)return 0;
	int ans=0;
	if(bloc[a]==bloc[b]){for(int i=a;i<=b;i++)ans+=vis[i];return ans;}
	for(int i=a;i<=br[bloc[a]];i++)ans+=vis[i];
	for(int i=bl[bloc[b]];i<=b;i++)ans+=vis[i];
	for(int i=bloc[a]+1;i<=bloc[b]-1;i++)ans+=sum1[i];
	return ans;
}
void add(int x){modify(a[x],1);}		//莫队加，值域增加数a[x]
void del(int x){modify(a[x],-1);}		//莫队减，值域删除数a[x]
map<int,int>t;int tot,l,r;
int main(){
	scanf("%d%d",&n,&m);block=1.0*n/sqrt(m)+1;
	for(int i=1;i<=n;i++)blo[i]=(i-1)/block+1;
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);maxx=max(maxx,a[i]);
	}
	B=sqrt(maxx);		//值域块大小
	for(int i=1;i<=maxx;i++)bloc[i]=(i-1)/B+1;blocknum=bloc[maxx];	//值域划分块
	for(int i=1;i<=blocknum;i++)bl[i]=(i-1)*B+1,br[i]=i*B;br[blocknum]=maxx;	//记每个值域块的左右边界
	for(int i=1;i<=m;i++){
		int x,y;
		scanf("%d%d%d%d",&x,&y,&l,&r);
		q[i].l=x;q[i].r=y;
		q[i].a=l;q[i].b=r;q[i].b=min(maxx,q[i].b);		//超过值域不用处理
		q[i].id=i;
	}sort(q+1,q+m+1,cmp1);
	l=1,r=0;
	for(int i=1;i<=m;i++){
		while(l<q[i].l)del(l++);
		while(l>q[i].l)add(--l);
		while(r<q[i].r)add(++r);
		while(r>q[i].r)del(r--);
		ANS[q[i].id]=query(q[i].a,q[i].b);	//查询第一个问题
		ANS2[q[i].id]=query2(q[i].a,q[i].b);//查询第二个问题
	}
	for(int i=1;i<=m;i++)printf("%d %dn",ANS[i],ANS2[i]);
	return 0;
}

例题

Rmq Problem / mex

同上面例题差不多，记录值域中的数有没有出现过，记录值域块是否全部数出现过

如果值域块中全部数都出现过，打一个标记，表示可以跳过该块

否则对该块进行查找，找到最小没有出现过的数

值域块也是从小到大枚举。

$blolen[i]$表示块$i$的长度，用来判断是否全部值域都出现过。

void modify(int x,int val){
	num[x]+=val;sum[bloc[x]]+=val;
	if(num[x]==1&&val==1)vis[x]=1,sum1[bloc[x]]++;
	if(num[x]==0&&val==-1)vis[x]=0,sum1[bloc[x]]--;
	if(sum1[bloc[x]]==blolen[bloc[x]])flag[bloc[x]]=1;else flag[bloc[x]]=0;//标记块
}
int query(){
	int ans=0,be=0;
	for(int i=1;i<=blocknum;i++)if(flag[i]==0){be=i;break;}	//如果不是全部出现过，就弹出
	if(be==0)return maxx+1;		//如果整个值域都出现过
	for(int i=bl[be];i<=br[be];i++)if(vis[i]==0){ans=i;break;}	//查找最小未出现值
	return ans;
}

曼哈顿交易

值域分块的另一种应用，查寻区间第$k$小

我们的值域是彩票出现次数

查询方法和平衡树查询区间第$k$小差不多

void modify(int x,int val){num[x]+=val;sum[blo[x]]+=val;res+=val;};
int query(int x){
	if(res<x)return -1;		//没有第k小
	for(int i=1;i<=block;i++){
		if(x>sum[i]){x-=sum[i];continue;}	//第k小不在当前块，跳下一个块
		for(int j=bl[i];j<=br[i];j++)		//第k小在当前块
		if(x>num[j])x-=num[j];
		else return j;		//找到第k小
	}
}
void add(int x){if(vis[a[x]])modify(vis[a[x]],-1);vis[a[x]]++;modify(vis[a[x]],1);}
void del(int x){modify(vis[a[x]],-1);vis[a[x]]--;if(vis[a[x]])modify(vis[a[x]],1);}

讲得不是很清，可以看题解区花姐姐的题解

带修莫队

例题：[国家集训队]数颜色 / 维护队列

题意：给出一个长为$N$的序列，$M$个操作$mode,x,y$，分为修改($mode=1$)和查询($mode=2$)，对于修改：将$x$位置的值改为$y$；对于询问：查询$[x,y]$中有多少个不同的数字。

我们可以发现，上面的例题没有一道是有修改的，难道莫队只能做无修的题吗？

NoNoNo

我们加一个时间维来解决~~（没有什么问题是加维解决不了的，如果有，就再加一维~~

首先，我们将修改和询问分开。

对于询问，我们记录以下值：

struct kkk{
	int l;	//左端点
	int r;	//右端点
	int t;	//此询问前修改数量
	int id;	//询问编号
}q[maxn];

对于修改，我们记录以下值：

struct ttt{
	int id;	//修改位置
	int val;//修改值
}c[maxn];

输入：

for(int i=1;i<=m;i++){
    bool mode;mode=readc();	//快读字符
    l=read();r=read();
    if(mode==1){		//询问
        qnum++;			//询问数
        a[qnum].l=l;a[qnum].r=r;
        a[qnum].t=rnum;a[qnum].id=qnum;	//记录t和id
    }else{				//修改
        rnum++;			//修改数
        c[rnum].id=l;c[rnum].val=r;
    }
}

然后对询问排序，由于多了一个关键字，于是乎变为三关键字排序，$l,r,t$的顺序

处理时我们多加一个指针$now$，表示已完成多少个修改

对于每个查询操作，如果当前时间$now$相对大了，说明已进行的修改操作比要求的多，就把之前改的改回来，反之往后改。只有当当前区间和查询区间左右端点、时间戳均重合时，才认定区间完全重合，此时的答案才是本次查询的最终答案。

在移动左右指针前，我们先对修改进行处理。

如果此时$now$比$a[i].t$小，那么时光推移，增加修改

如果此时$now$比$a[i].t$大，那么时光倒流，把之前的修改抹去

那如何增加或抹去修改？

我们先将原来值对答案的影响抹去，再将修改值对答案的影响加上，然后更新该位置的值

#define add(x) if(++vis[x]==1)sum++;
#define del(x) if(--vis[x]==0)sum--;
void change(int x){
	if(c[x].id>=l&&c[x].id<=r){del(v[c[x].id]);add(c[x].val);}	//改变影响
	swap(c[x].val,v[c[x].id]);		//值更新 *
}
……
while(now<q[i].t)change(++now);	//修改
while(now>q[i].t)change(now--);	//修改

*注：del和add函数和询问的函数一致

询问和先前一样，不需要修改。

不过有个代码长度的小优化——移完 $now$，做完一处修改后，有可能要改回来，所以我们还要把原值存好备用。但其实我们也可以不存，只要在修改后把修改操作的值和原值swap一下，那么改回来时也只要swap一下，swap两次相当于没搞，就改回来了QwQ (从别人那学的)

提醒：此题有点卡常，要修改块大小

带修莫队块大小要多大才最快？

明显，除了询问的移动，我们还要考虑修改的移动，所以普通莫队的块大小会在带修莫队中没有优秀的表现。

那么怎么样的块大小才适合呢？

给出几种块大小：$n^{\frac{2}{3}}$ 、$\sqrt[3]{nt}$（理论最优，对于此题慢得一匹（可能是我写太丑了））、自己调（例如下面代码

至于证明嘛，我不会哦~

#include<bits/stdc++.h>
#define maxn 135001 
using namespace std;
struct kkk{
	int l;	//左端点
	int r;	//右端点
	int t;	//此询问前修改数量
	int id;	//询问编号
}q[maxn];
struct ttt{
	int id;	//修改位置
	int val;//修改值
}c[maxn];
bool readc(){		//读字符
	char ch=getchar();
	while(ch!='Q'&&ch!='R')ch=getchar();
	return ch=='Q';
}
int read(){
	int x=0;char ch=getchar();
	while(ch<48||ch>57){ch=getchar();}
	while(ch>=48&&ch<=57){x=x*10+(ch^48);ch=getchar();}
	return x;
}
int blo[maxn],block,n,m,l,r,now,sum,v[maxn],vis[1020001],ANS[maxn];
int qnum,rnum;
bool cmp(const kkk &a,const kkk &b){
	if(blo[a.l]!=blo[b.l])return a.l<b.l;
	if(blo[a.r]!=blo[b.r])return (blo[a.l]&1)?(a.r<b.r):(a.r>b.r);
	return a.t<b.t;
}
#define add(x) if(++vis[x]==1)sum++;
#define del(x) if(--vis[x]==0)sum--;
void change(int x){
	if(c[x].id>=l&&c[x].id<=r){del(v[c[x].id]);add(c[x].val);}	//改变影响
	swap(c[x].val,v[c[x].id]);		//值更新
}
int main(){
	n=read();m=read();block=10; while(1ll*block*block*block<=1ll*n*n*3)block++;//YYC大佬YY的块大小，跑得飞快
	for(int i=1;i<=n;i++)v[i]=read();
	for(int i=1;i<=n;i++)blo[i]=i/block;
	for(int i=1;i<=m;i++){
		bool mode;mode=readc();
		l=read();r=read();
		if(mode==1){
			qnum++;
			q[qnum].l=l;q[qnum].r=r;
			q[qnum].t=rnum;q[qnum].id=qnum;
		}else{
			rnum++;
			c[rnum].id=l;c[rnum].val=r;
		}
	}
	sort(q+1,q+qnum+1,cmp);
	l=1;r=0;now=0;
	for(int i=1;i<=qnum;i++){
		while(now<q[i].t)change(++now);
		while(now>q[i].t)change(now--);
		while(l>q[i].l)add(v[--l]);
		while(l<q[i].l)del(v[l++]);
		while(r<q[i].r)add(v[++r]);
		while(r>q[i].r)del(v[r--]);
		ANS[q[i].id]=sum;
	}
	for(int i=1;i<=qnum;i++)
	printf("%dn",ANS[i]);
	return 0;
}

问题：如果我们在移动左右指针后再对修改进行处理，会不会影响结果或时间复杂度？

个人见解：

其实对结果是不会影响的……

因为修改对答案的影响有调整

但对时间复杂度会有影响

至于是更优还是更劣

看数据决定了…… 事实证明，某些情况下会更快一点

树上莫队

传说什么数据结构都能上树，莫队也可以！

引入：SP10707 COT2 - Count on a tree II

题目描述： 给定一个n个节点的树，每个节点表示一个整数，问u到v的路径上有多少个不同的整数。

通常情况，我们对树上的区间问题都使用$dfs$序来转化为序列问题，我们来试试

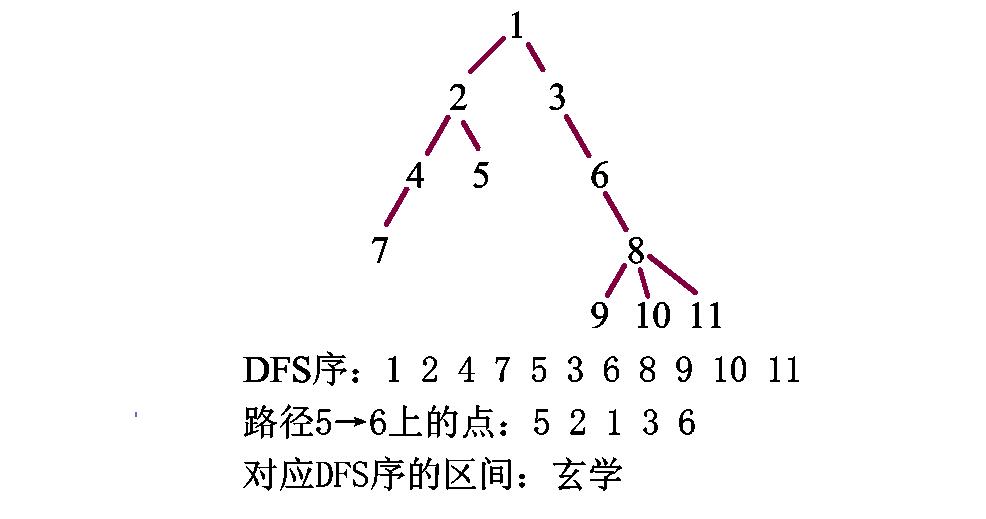
参照此图，明显：普通$dfs$序是完全不行的（因为区间没有对应关系）。

欧拉序

性质：

1.每一个点出现了两次

2.两个相同点之间出现的点是该点子数上的点，并且出现两次

欧拉序求法：DFS到一个点时加入序列，退出时也加入一遍。

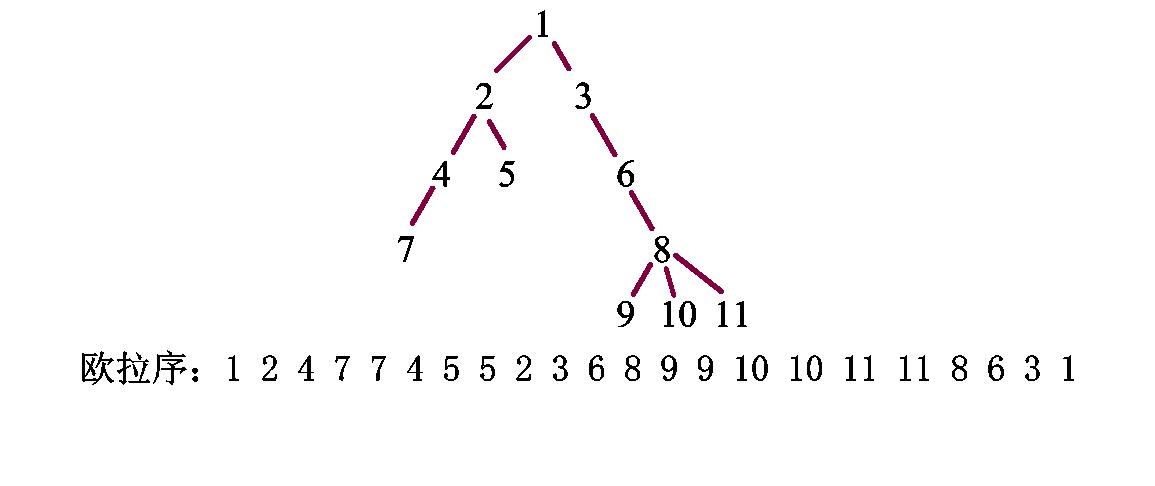
欧拉序有什么用呢？举两个例子，看图：

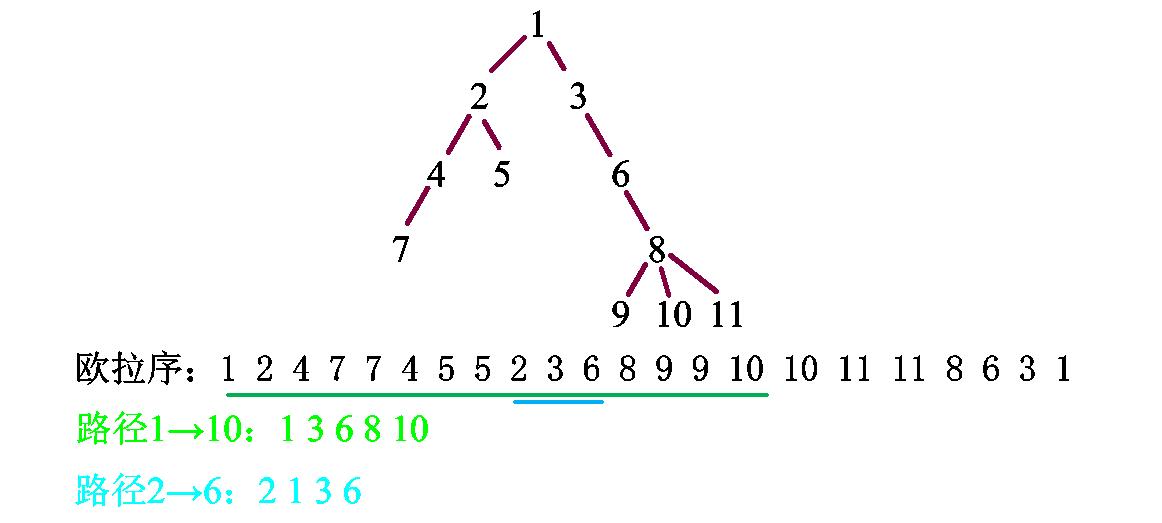
我们发现绿色范围中出现次数为$1$的点正好对应树上要求的点

蓝色范围处理$LCA$也就是$1$没有出现，也满足出现次数为$1$的点正好对应树上要求的点

具体做法：设每个点的编号$a$首次出现的位置$first[a]$，最后出现的位置为$last[a]$，那么对于路径$x\to y$，设$first[x]<=first[y]$，如果$lca(x,y)=x$，则直接把$[first[x],first[y]]$的区间扯过来用，反之使用$[last[x],first[y]]$区间（为什么不用$[first[x],first[y]]$？因为$(first[x],last[x])$不会在路径上，根据性质，里面的编号都会出现两次，考虑了等于没考虑），但这个区间内不包含$x$和$y$的最近公共祖先，查询的时候单独加上即可。

注意：序列长度为$2\ast n$

做完了这些，树上莫队的其他东西就和普通莫队差不多啦。值得注意的是，我们又可以像上文的带修莫队那样优化代码长度——由于无需考虑的点会出现两次，我们可以弄一个标记数组（标记结点是否被访问），没访问就加，访问过就删，每次操作把标记·异或个1，完美解决所有添加、删除、去双问题。

算法流程：

1.建树，跑dfs求出欧拉序和first,last

2.对于每一个询问，求出他们在欧拉序下的对应左右区间，和上文提的方法一样

3.正常莫队排序

4.正常莫队处理，如果要加上Lca记得加，统计完答案要把加的Lca撤回

5.正常输出

---

P4074 [WC2013]糖果公园

题意：

给出三个正整数 $n,m,q$， 分别表示点个数、 点种类数和操作次数。

给出 $n$ 个正整数 $V_1,V_2,\dots ,V_m$。表示$i$种类点的价值

给出 $m$ 个正整数 $W_1,W_2,\dots ,W_n$。表示某种类点出现第$i$次的加成数

给出$n-1$行，每行包含两个正整数 $A_i,B_i$，表示这两个点之间有路径可以直接到达。

给出 $n$ 个正整数 $C_1,C_2,\dots ,C_n$。表示第$i$个点的种类数

$q$ 个询问， 每行包含三个整数 $Type,x,y$ 表示一次操作：

若 $Type$ 为 $0$，则 $1\le x\le n$，$ 1 ≤ y ≤ m$，表示将编号为 $x$ 的点的种类改为 $y$；

若 $Type$ 为 $1$，则 $1\le x,y\le n$，表示对出发点为$ x$ ，终止点为$ y $的路线询问答案。

对于每个点，记它的种类为$x$，它是该路径上第$y$个出现的$x$种类点，它的权值为$V_a\ast W_y$

答案即为该路径上的点权和。

解法：

港真，这题没有什么思维难度，莫队的转移大家应该很快都能想到

所以这题就是树上带修莫队的模板题，把树上莫队和带修莫队结合一下就好了

主要是考验大家对树上莫队和带修莫队是否真正理解

额，真的没什么好讲的，记得开longlong

其实这题还有一个作用，考验你的卡常能力

过了不算什么，要把总时间压缩到3~5s内，这才达到这题的价值

这样你能学到不少莫队的压缩时间的技巧，这里就不一一讲了

卡常吧，少年！

回滚莫队

用于解决你会加入但不会删除的莫队（或者加入简单，删除太复杂的莫队）

也就是不删除的莫队

给道模板题：P5906【模板】回滚莫队&不删除莫队

此时，由于莫队的无敌（雾），有神犇发明了一个玄学高效的算法，复杂度最坏$O(n\sqrt{n})$，而且常数碾压同为$O(n\sqrt{n})$的块状数组做法。

我们观察莫队的性质：左端点在同一块中的所有查询区间右端点单调递增。这样，对于左端点在同一块中的每个区间，我们都可以$O(n)$解决所有的右端点，且不用回头删除值（单调递增）。考虑枚举每个块，总共需要枚举$O(\sqrt{n})$个块，这部分的总复杂度$O(n\sqrt{n})$。

又对于每个块内的左端点：假设每个块内的每个左端点都从块右端开始统计，每次都重新开始暴力统计一次，做完每个左端点复杂度$O(\sqrt{n})$，共$n$个左端点，总复杂度$O(n\sqrt{n})$。

我们发现这两部分是很容易结合起来的。做法就是枚举每个块，每次把$l,r$指针置于块尾+1的位置和块尾（至于为什么+1还请看前面），先暴力处理掉左右端点在一块的特殊情况（$O(\sqrt{n})$），然后右端点暴力向右推，左端点一个个解决，在移动左指针前纪录一下当前状态，移动保存值后复原即可，也无需删除。以上的问题完美解决。

以上引用别人博客

代码：

#include<bits/stdc++.h>
#define maxn 4000001
using namespace std;
struct kkk{
	int l,r,id;int ans;
}a[maxn];
int ans;
int blo[maxn],block,n,m,v[maxn],la[maxn],st[maxn],vis[maxn],cl[maxn],cn;
bool cmp1(kkk a,kkk b){return a.id<b.id;}
bool cmp(kkk a,kkk b){
	if(blo[a.l]!=blo[b.l])return a.l<b.l;
	else return a.r<b.r;
}
void add(int x,int mode){			//加值
	if(mode==1){
		la[v[x]]=x;
		if(!st[v[x]])st[v[x]]=x,cl[++cn]=v[x];	//cl数组记录右端点修改位置
		ans=max(ans,x-st[v[x]]);
	}else{
		if(la[v[x]])ans=max(ans,la[v[x]]-x);
		else la[v[x]]=x;
	}
}
int query(int l,int r){				//单独暴力查询
	int maxx=0;
	for(int i=l;i<=r;i++)vis[v[i]]=0;
	for(int i=l;i<=r;i++){
		if(vis[v[i]]!=0)maxx=max(maxx,i-vis[v[i]]);
		else vis[v[i]]=i;
	}
	return maxx;
}
void roll(int x){if(la[v[x]]==x)la[v[x]]=0;}	//回滚
int solve(int qnum,int id){
	int L=min(id*block,n);
	int l=L+1,r=l-1;cn=0;int i=qnum;
	ans=0;
	for(;blo[a[i].l]==id;i++){
		if(blo[a[i].r]==id){a[i].ans=query(a[i].l,a[i].r);continue;}
		while(r<a[i].r)add(++r,1);		//右端点移动
		int jc=ans;
		while(l>a[i].l)add(--l,2);		//左端点移动
		a[i].ans=ans;
		while(l<=L)roll(l++);		//滚去左端点
		ans=jc;	//复原答案
	}
	for(int j=1;j<=cn;j++)la[cl[j]]=st[cl[j]]=0;	//清0，防对下一个块有影响
	return i;
}
map<int,int>t;int tot,blocknum;
int main(){
	//freopen("P5906.in","r",stdin);
	//freopen("5906.out","w",stdout);
	scanf("%d",&n);block=sqrt(n);
	for(int i=1;i<=n;i++){
		int x;
		scanf("%d",&x);
		if(!t.count(x))t[x]=tot++;
		v[i]=t[x];
	}
	scanf("%d",&m);
	for(int i=1;i<=n;i++)blo[i]=(i-1)/block+1; blocknum=blo[n];
	for(int i=1;i<=m;i++){
		scanf("%d%d",&a[i].l,&a[i].r);
		a[i].id=i;
	}
	sort(a+1,a+m+1,cmp);
	int qnum=1;
	for(int i=1;i<=blocknum;i++){
		qnum=solve(qnum,i);		//处理块
	}
	sort(a+1,a+m+1,cmp1);
	for(int i=1;i<=m;i++)printf("%dn",a[i].ans);
}

练习：AT1219 歴史の研究

一样是修改简单查询难，套上回滚莫队的模板即可

#include<bits/stdc++.h>
#define maxn 1000001
using namespace std;
struct kkk{
	int x,y,id,flag;
	long long ans;
}a[maxn];
struct ggg{
	int a,b,p;
}a1[maxn];
int block,blo[maxn],v[maxn],vis[maxn],aa[maxn];
int Vis[maxn],pos;
int n,m,l,r;
long long maxx;
bool cmp1(ggg a,ggg b){
	return a.a<b.a||(a.a==b.a&&a.p<b.p);
}
bool comp(kkk a,kkk b){
	return a.id<b.id;
}
bool cmp(kkk a,kkk b){
	if(blo[a.x]!=blo[b.x])return a.x<b.x;
	return a.y<b.y;
}
void add(int x){
	vis[v[x]]++;maxx=max(maxx,(long long)vis[v[x]]*aa[x]);
}
void roll(int x){vis[v[x]]--;}
long long check(int l,int r){
	long long maxy=0;
	for(int i=l;i<=r;i++)Vis[v[i]]=0;
	for(int i=l;i<=r;i++){
		Vis[v[i]]++;
		maxy=max(maxy,(long long)Vis[v[i]]*aa[i]);
	}
	return maxy;
}
int Mo(int pos,int bl){
	maxx=0;int last=0,i=pos;
	for(int j=1;j<=n;j++)vis[j]=0;
	int L=min(block*bl,n);
	int l=L+1,r=L;
	for(;blo[a[i].x]==bl;i++){
		if(blo[a[i].x]==blo[a[i].y]){a[i].ans=(long long)check(a[i].x,a[i].y);continue;}
		while(r<a[i].y){add(++r);}
		last=maxx;
		while(l>a[i].x){add(--l);}
		a[i].ans=maxx;
		while(l<L+1)roll(l++);
		maxx=last;
	}
	return i;
}
int main(){
	int num;
	scanf("%d%d",&n,&m);block=sqrt(n);
	for(int i=1;i<=n;i++){scanf("%d",&a1[i].a);aa[i]=a1[i].a;a1[i].p=i;}  //离散化
	for(int i=1;i<=n;i++)blo[i]=(i-1)/block+1;num=blo[n];
	sort(a1+1,a1+n+1,cmp1);
	for(int i=1,j=0;i<=n;i++){
		if(i==1||a1[i].a!=a1[i-1].a)j++;
		v[a1[i].p]=j;       //离散化后数组
	}
	for(int i=1;i<=m;i++){
		scanf("%d%d",&a[i].x,&a[i].y);
		a[i].id=i;
	}
	pos=1;
	sort(a+1,a+m+1,cmp);
	for(int i=1;i<=num;i++){
		pos=Mo(pos,i);
	}
	sort(a+1,a+m+1,comp);
	for(int i=1;i<=m;i++){
		printf("%lldn",a[i].ans);
	}
	return 0;
}

二次离线莫队

太难了，暂时不想写，到时候熟练了再写

结语

那么莫队讲到这里就差不多了，相信大家一定都有收获

来总结一下：

莫队算法是区间利器，它可以解决很多离线的条件不那么苛刻的区间问题

总之就是非常厉害

但莫队受到只能离线的限制，因此其他区间算法还是很重要（在线莫队/jk

本篇文章收集许多网上博客整合而成，应该算是很详细的了（自夸

当然提升还是要靠多刷题

所以这里我又给大家准备几道题：

莫队细讲题单

完成上面的题单大概就差不多了

[SNOI2017]一个简单的询问（化式子+莫队）

[SCOI2012]喵星球上的点名（SA+莫队）

[LnOI2019]来者不拒，去者不追（二次离线莫队

『MdOI R1』Path（回滚莫队+01Trie）

「Wdoi-1」完美冻结（二次离线莫队）

完结撒花❀

$Finsih$

屁

莫队比我想的毒瘤多了

莫队的扩展

在线莫队

二维莫队

回滚莫队拓展

最后

以上就是无辜可乐为你收集整理的莫队细讲——从零开始学莫队莫队更好的阅读体验例题莫队套分块带修莫队树上莫队回滚莫队二次离线莫队结语莫队的扩展的全部内容，希望文章能够帮你解决莫队细讲——从零开始学莫队莫队更好的阅读体验例题莫队套分块带修莫队树上莫队回滚莫队二次离线莫队结语莫队的扩展所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。