CCF-201312-3-最大的矩形

63 阅读 0 评论 42 点赞

我是靠谱客的博主悦耳衬衫，最近开发中收集的这篇文章主要介绍CCF-201312-3-最大的矩形，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

题目：
问题描述
　　在横轴上放了n个相邻的矩形，每个矩形的宽度是1，而第i（1 ≤ i ≤ n）个矩形的高度是hi。这n个矩形构成了一个直方图。例如，下图中六个矩形的高度就分别是3, 1, 6, 5, 2, 3。

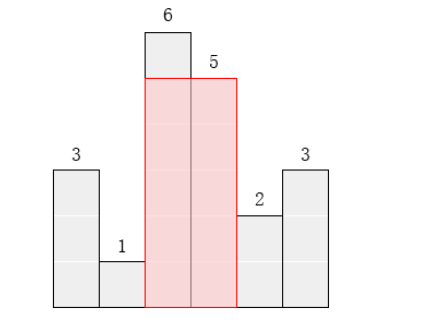
在这里插入图片描述

请找出能放在给定直方图里面积最大的矩形，它的边要与坐标轴平行。对于上面给出的例子，最大矩形如下图所示的阴影部分，面积是10。
输入格式
　　第一行包含一个整数n，即矩形的数量(1 ≤ n ≤ 1000)。
　　第二行包含n 个整数h1, h2, … , hn，相邻的数之间由空格分隔。(1 ≤ hi ≤ 10000)。hi是第i个矩形的高度。
输出格式
　　输出一行，包含一个整数，即给定直方图内的最大矩形的面积。
样例输入
6
3 1 6 5 2 3
样例输出
10
这道题乍一看想到动态规划，但结果发现做不出来，看了一下以前写的代码，实际可以这样做（如果下一段看不懂的话直接跳过看再下一段）：
因为题目说了要使连续的几个矩形组成的最大面积，直接换个方向来想，就把所有的边都给测试出来，设置两个循环，第一个循环把所有的边的高度矩形的高度，第二个循环检查以该边为高度下能有几个连续的矩形，当检查到该边比指定高度小时就看前几个矩形组成的面积是否比最大面积大，比最大面积大就记录下来，然后面积归零，从下一个位置又开始以该高度进行计算。
简单来说看下图：
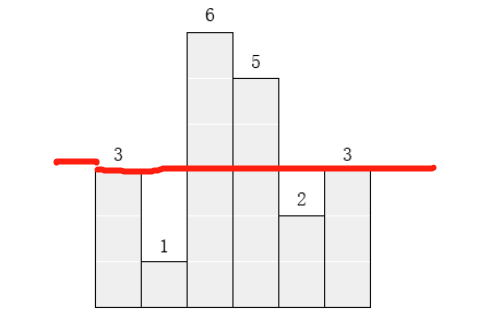
在这里插入图片描述

首先以a[0] 即3为高，对整个数组进行检查，
第一个a[0]=3，可以加到面积上去，
a[1]=1<3，放弃该边并比较前面统计出来的面积是否比最大面积大，当前面积比最大面积大就修改最大面积，
然后从a[2]又重新开始统计面积，a[2],a[3]都可以以3为高，可以加到面积上去，即执行步骤2，得到面积为6，到a[4]=2<3,执行过程如（3）
通过以上一趟循环就算出以a[0]=3为高时能得到的矩阵的最大面积，然后i增1，以a[1]为高再执行以上1~4过程如下图

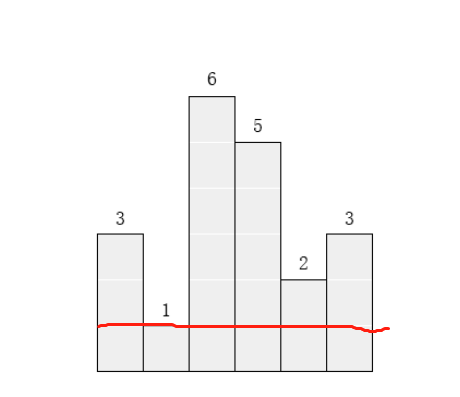
通过以上计算就能得出以每一个矩阵的高度为直方图矩阵高度时的面积，从而得出最大面积。总结起来就一句话，以每一个高度为矩阵高度都去试一试。
代码如下：

#include<iostream>
using namespace std;
int main(){
	int m;
	cin>>m;
	int a[m];
	int b[m];
	for(int i=0;i<m;i++){
		cin>>a[i];
		b[i]=a[i];
	}
	
	int maxarea=0;
//	先对a数组进行排序，然后看最大面积
	for(int i=0;i<m;i++){
		int area=0;
		for(int j=0;j<m;j++)//注意这里不能从i开始，因为虽然a在递增但b是无序的 每一个b[j]即可能比a[i]大也可能比他小
		{
			if(b[j]>=a[i]) area+=a[i];//相当于直接以每一个高度来进行计算
			else{
				if(area>maxarea) maxarea=area;
				area=0;
			} 
		 } 
		if(area>maxarea) maxarea=area;
	} 
	cout<<maxarea;
}