深度学习科学炼丹

本文主要记录一些深度学习中的一些trick的使用及其原因 不定期更新

为什么激活函数更喜欢ReLU而不是tanh或者sigmoid

当我们网络比较深的时候，ReLU往往表现更好，因为ReLU只有一个拐点，而tanh/sigmoid有两个拐点（这里叫拐点不太准确），之后曲线就都趋近于平缓，这可能会导致梯度消失的问题，当输入到激活函数的值很大或很小时，会导致在反向传播的时候会导致这部分的导数很小，使得该部分前面的网络无法训练。

对输入进行normalize

一般来说应该在训练前，对于训练集做归一化，使训练数据的每个维度的均值为0。
举例来说，对于一个神经网络的输入，如果某层节点的输入始终为正数，那么在更新与该结点连接的权重的时候，假设该结点的输出为$a_i$，那么梯度为$\frac{\partial L}{\partial a_i}{x}_i$，因为$x_i$始终为正，那么更新方向就完全取决于$\frac{\partial L}{\partial a_i}$的方向，而这可能会导致zigzag的更新方式，更新效率低下。
使得训练数据的各个维度的方差相同/相似，一般可调整为1。
如果不同的维度的数据尺度大小相差很多，那么各权重还要学着去适应不同维度的大小尺度，除非有一些维度已知的没那么重要，那么可以相对的使其scale小一些，降低它在学习过程中的重要性。

降低神经网络各结点输入值的相关性

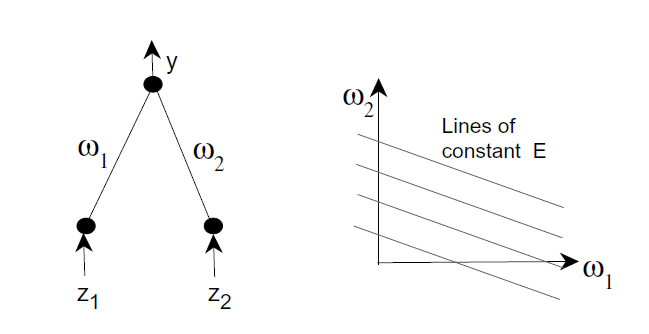
如下图左所示，如果输入$z1$和$z2$线性相关，假设$z2$的输入始终为$z1$输入的两倍，即$y=w_1{z}_1+w_2{z}_2=w_1{z}_1+2w_2{z}_1$等价于$w_1+2w_2=\frac{y}{z_1}$，根据输入$z_1$的变化，$w_1$与$w_2$的关系始终满足下图右中的某一条直线，所以当$w_1$与$w_2$满足某条直线的时候，而沿着该直线的更新就没有用处了，所以在一个2-D范围内，很容易造成很多无效的更新，增长训练时间。

在参数训练时对参数加上L1/L2正则化，在训练一段时间之和再开始做正则化

$L=c(w)+\alpha R(w)$
$w_i=w_i-\eta \frac{\partial L}{\partial w_i}=w_i-\eta (\frac{\partial c}{\partial w_i}+\alpha \frac{\partial R}{\partial w_i})$
对于$L2$正则化，$R(w)=||w|{|}^2$
所以$w_i=w_i-\eta (\frac{\partial c}{\partial w_i}+\alpha \ast 2w_i)=(1-2\alpha \eta )w_i-\eta \frac{\partial c}{\partial w_i}$
相当于在每一个更新权重的时候，为$w_i$乘上一个小于1的权重

对于$L1$正则化，$R(w)={\Sigma }_i|w_i|$
所以$w_i=w_i-\eta (\frac{\partial c}{\partial w_i}+\alpha sign(w_i))$

为什么在开始训练一段时间之后再做正则化
因为weight space的原点类似于loss function的一个saddle point，如果一开始就做正则化的话，可能会导致weights都变成0，然后网络就不会work了，所以这也说明了权重正确初始化的重要性。

CNN网络擅长处理什么

CNN网络擅长处理的图片最好有以下三个性质

Locality
一般对于一张图片来说，相邻的像素往往可能有着相似的颜色，随着像素间距离的增大，这种相似的可能性也随之下降，这种小范围内的相似性有利于CNN去挖掘pattern

Stationarity
相同的pattern可以在图片的任何地方出现

Compositionality
图像是由各pattern层级组成的，和网络中的多层神经元相对应，后面的神经元能够从前面神经元的输出从更大的感受野中提取信息

Activation Functions

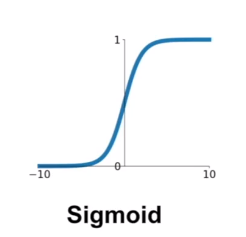
Sigmoid的问题：
（1）梯度消失，对于较正或者较负的输入，在反向传播的时候，梯度接近是0
（2）输出不是zero-centered，原因和为什么一般要对输入进行normalize是一样的
（3）exp()运算的计算代价

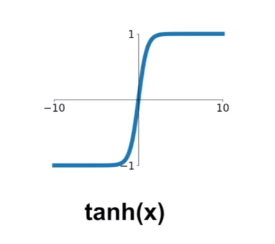
tanh的问题：
（1）同sigmoid一样的梯度消失的问题

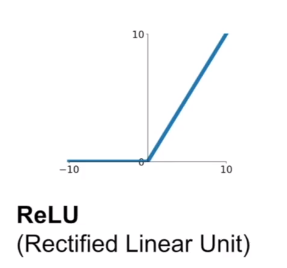
ReLU
（1）在正向不会有梯度消失
（2）计算代价低，收敛快
（3）输出不是zero-centered
（4）负向仍然存在梯度消失的问题（不好的weights初始化；学习率过高，梯度对weights的更新太大）

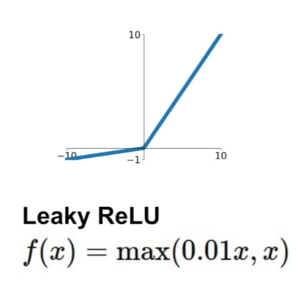
Leaky ReLU
（1）没有梯度消失的问题
（2）一定程度上解决输出不是zero-centered的问题
（2）PReLU：$f(x)=max(\alpha x,x)$，相当于把Leaky ReLU的0.01参数化了

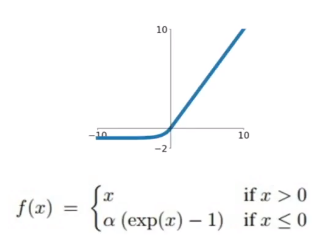
ELU：
（1）对离群点有一定的鲁棒性，因为在负向随着$x$变小梯度会逐渐消失
（2）一定程度上解决输出不是zero-centered的问题

参考资料：
Neural Networks Tricks of the Trade
NYU《deep learning》course 2020
CS231n

最后

以上就是称心大树为你收集整理的深度学习科学炼丹的全部内容，希望文章能够帮你解决深度学习科学炼丹所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。