J - Jumping frog Gym - 101889J（gcd，置换）

题意：
R可与走，P不可以走。
可以任选起点，每步的长度为k。
求问存在多少k，使得你最后可以跳回起点。
从i跳一步后会变成(i+k)%n

思路：
感觉和之前写过的置换很像，也是在环上跳。

对于所跳的步长k，如果gcd(n,k)=1，那么实际就是要遍历每一个点，必须得满足所有点都是R。
否则的话，最终要跳$n\ast k/gcd(n,k)/k=n/gcd(n,k)$步。这里有一个结论，对于$k1,k2$,如果$gcd(n,k1)=gcd(n,k2)$，那么起点相同时，步长为$k1$或者$k2$进行跳跃得到的点集数一样的，所以与$n$的$gcd$相同的数可以合并一起统计。或者说，对于步长$k$，我们只需要考虑前$gcd(n,k)$个起点。所以知道步长以后，枚举起点模拟跳的复杂度为$O(n)$

证明：
假设存在$gcd(n,k1)=gcd(n,k2)$，
不妨设$k1|n$，则可以得到$k1|k2$，
当起点确定，步长分别为$k1,k2$时，两者跳跃的循环长度都为$n/gcd(n,k1)$，
而又有$k1|k2$，所以步长$k2$时能跳到的点一定包含于步长$k1$时能跳到的点，
而两者步数又一样，
所以得证两者跳跃得到的点集一样。

所以我们枚举n的所有约数（互质直接判断），然后枚举起点模拟一直跳就好了；其他的数要么是n的约数的倍数（约数可以，则倍数一定可以），要么就和n互质。
（这里直接枚举了所有与n的gcd不为1的数，感觉复杂度有点假，但是过了）。

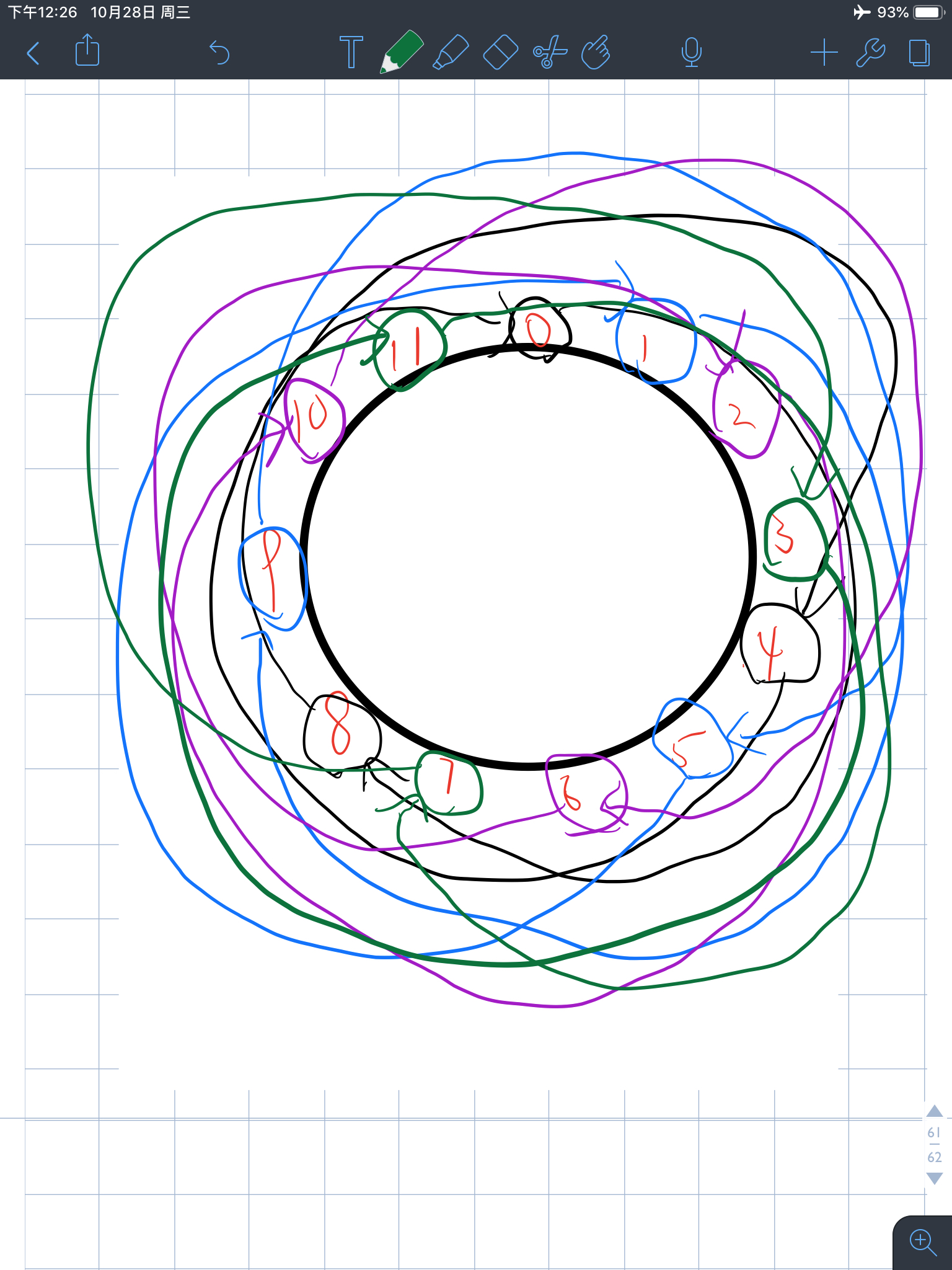
（图凑合看吧，就是表达一个意思）
此时k=8,n=12
0->8->4->0
1->9->5->1
2->10->6->2
3->11->7->3

#include <bits/stdc++.h>
#define lson (id<<1)
#define rson (id<<1|1)
using namespace std;
const int maxn = 1e5+10;
typedef long long ll;

char s[maxn];

int gcd(int n,int m) {
    return m == 0 ? n : gcd(m,n % m);
}

int main() {
    scanf("%s",s);
    int n = strlen(s);
    int flag = 1;
    for(int i = 0;i < n;i++) {
        if(s[i] == 'P') {
            flag = 0;break;
        }
    }

    int ans = 0;
    for(int i = 1;i < n;i++) {
        int num = gcd(i,n);
        if(num == 1) {
            if(flag) {
                ans++;
            }
        } else {
            bool ok = 1;
            for(int j = 0;j < num;j++) {
                ok = 1;
                int sta = j;
                while(1) {
                    if(s[sta] == 'P') {
                        ok = 0;break;
                    }
                    sta = (sta + i) % n;
                    if(sta == j) break;
                }
                if(ok) break;
            }
            if(ok) ans++;
        }
    }

    printf("%dn",ans);
    return 0;
}

最后

以上就是甜甜板栗为你收集整理的J - Jumping frog Gym - 101889J（gcd，置换）的全部内容，希望文章能够帮你解决J - Jumping frog Gym - 101889J（gcd，置换）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。