Step1 Problem:
给你 n 个盒子,每个盒子里面有 f[i] 朵花,不同盒子花不一样,同一个盒子花一样,求从这 n 个盒子选出 s 朵花得方案数
数据范围:
1 <= n <= 20, 0 <= s <= 1e14, 0 <= fi <= 1e12.
Step2 Ideas:
逆元学习地方
a * x ≡ 1(mod p)。
因为p是素数,所以我们求逆元可以用费马小定理 和 欧拉定理
a^(p-1) ≡ 1(mod p) -> a*a^(p-2) ≡ 1(mod p)。所以a^(-1) = a^(p-2)还有一种通用的求逆元方法,适合所有情况。公式如下
现在我们来证明它,已知,证明步骤如下
Lucas定理
那么得到
这样然后分别求,采用逆元计算即可。
这题学习博客
从 n 个盒子选花,有的盒子可以不选,组成 s 的方案数 可以转换为:
s 个球是无标志的,n 个盒子是由区别的,取 s 个球放进盒子,每个盒子允许多于一个球。
相当于有 s+n-1 个物品摆放着,我们从中选取 n-1 个当作隔板,被隔板隔开的物品就相当于每个盒子的球的数量。
从 n 个盒子选花,有的盒子可以不选,组成 s 的方案数 = C(s+n-1, n-1);
这题有 f[i] 的限制,这样计数的话某些花会超出其个数,我们可以进行容斥:
比如确定 i 超出个数其它不确定的方案 C(sum-(f[i]+1)+n-1,n-1)
因为 n <= 20, 所以我们可以二进制枚举确定哪些 i 超出容斥
所以 ans = 超0 - 超1 + 超2 - 超3 …
Lucas 适用于 n 和 m 很大,但是 MOD 不是特别大
这题可以不用 Lucas, 因为 n 很小
Step3 Code:
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int MOD = 1e9+7;
ll f[25];
ll Pow(ll a, ll n)//快速幂
{
ll sum = 1;
while(n)
{
if(n&1) sum = sum*a % MOD;
a = a*a % MOD;
n >>= 1;
}
return sum;
}
ll C(ll n, ll m)//c(n,m)
{
ll a = 1, b = 1;
if(m > n) return 0;
if(m > n/2) {
m = n-m;
}
if(m == 0) return 1;
for(ll i = 1; i <= m; i++)
{
a = a*(n+i-m) % MOD;
b = b*i % MOD;
}
return (a*Pow(b, MOD-2)%MOD)%MOD;//a*b^(-1)%MOD
}
ll Lucas(ll n, ll m)//Lucas定理 m <= n
{
if(!m) return 1;
return C(n%MOD, m%MOD) * Lucas(n/MOD, m/MOD) % MOD;
}
int main()
{
int n;
ll s;
scanf("%lld %lld", &n, &s);
for(int i = 0; i < n; i++)
scanf("%lld", &f[i]);
ll ans = 0;
for(int k = 0; k < (1<<n); k++)
{
ll sum = s; int flag = 0;
for(int i = 0; i < n; i++)
{
if((1<<i)&k) {
sum -= f[i]+1;
flag ^= 1;
}
}
if(sum < 0) continue;
if(!flag) {
ans += Lucas(sum+n-1, n-1); ans %= MOD;
}
else {
ans -= Lucas(sum+n-1, n-1); ans = (ans%MOD+MOD)%MOD;
}
}
printf("%lldn", ans);
return 0;
}
最后
以上就是甜甜荔枝最近收集整理的关于【组合数学 && 容斥 && C(n, m)%p && 逆元 && m 个大于等于 0 的数组成 k 的方案数】CodeForces - 451E Devu and Flowers的全部内容,更多相关【组合数学内容请搜索靠谱客的其他文章。
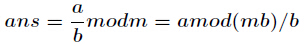
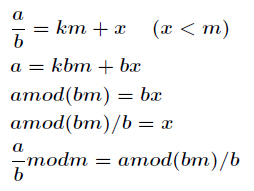
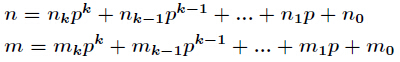
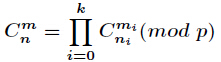








发表评论 取消回复