BP神经网络

目录

1、BP（Back propagation）神经网络描述

2、BP神经网络的向前传播

3、BP神经网络的代价函数（损失函数）

4、BP神经网络的反向传播

5、BP神经网络优化过程总结

6、BP神经网络的进一步优化

1、BP（Back propagation）神经网络描述

（1）BP（反向传播(Back Propagation)）神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络，是目前应用最广泛的神经网络之一。

（2）该网络的主要特点是信号的正向传播，误差反向传播

（3）BP神经网络主要分为两个过程：

     第一个过程是信号的正向传播（前向传播），从输入层经过隐藏层，最后到达输出层；

     第二个过程是误差的反向传播，从输出层到隐藏层，最后到输入层，依次调节隐藏层到输出层的权重和偏置，输入层到隐藏层的权重和偏置。

2、BP神经网络的向前传播

（1）前向传播算法的数学定义（偏置项和权重）（加权求和+激活函数）

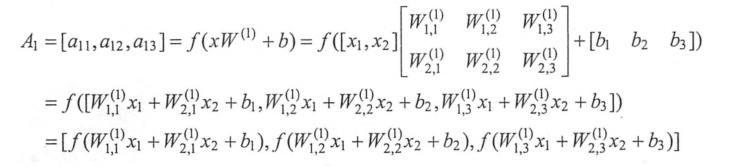
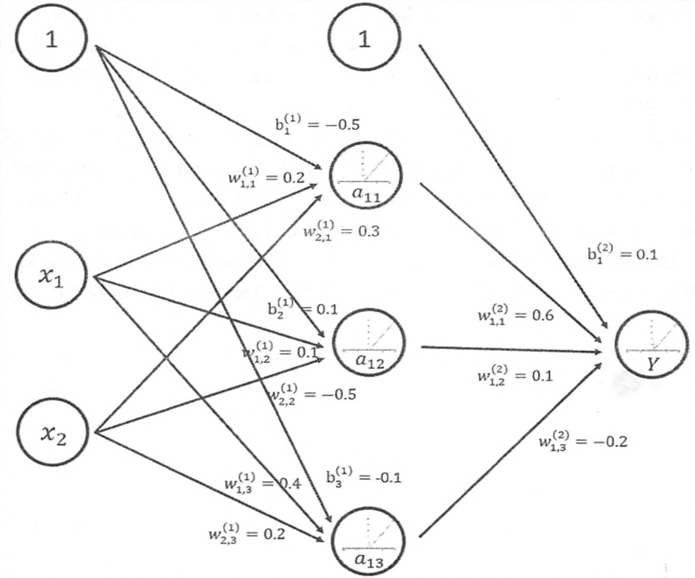
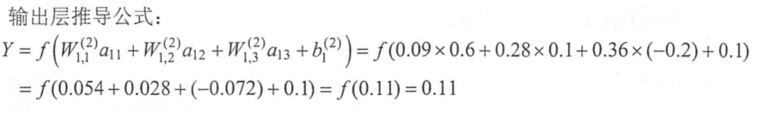
（2）偏置项和激活函数

• 偏置项：是神经网络中非常常用的一种结构，与线性方程 y=wx+b 中的 b 的意义是一致的，在 y=wx+b中，b表示函数在y轴上的截距，控制着函数偏离原点的距离。
• 激活函数：加入非线性因素，实现去线性化，解决线性模型不能解决的问题

常用激活函数如下：

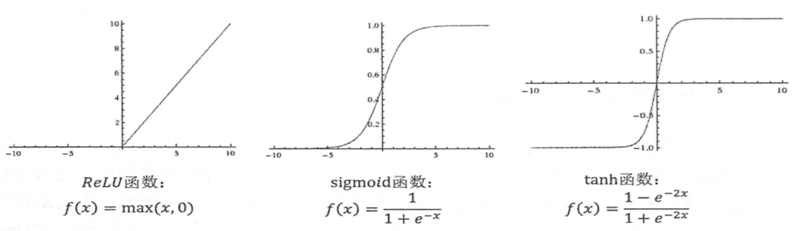
3、BP神经网络的代价函数（损失函数）

（1）二次代价函数（均方误差函数）

单变量线性回归二次代价函数

建模误差的平方和（预测值与真实值）

多变量线性回归二次代价函数

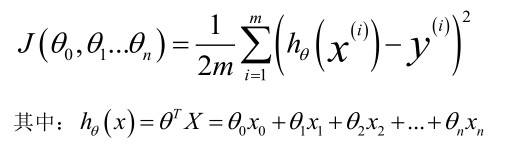
二分类问题和回归问题，一般用二次代价函数（均方误差函数）

    比如:

           对于判断零件是否合格的二分类问题，神经网络的输出层有一个节点。当这个节点越接近0时越有可能不合格，越接近1时越有可能合格。具体分类结果可以选择0.5作为阈值，小于0.5则不合格，大于0.5则合格。

神经网络解决多分类问题

    用n维数组作为输出结果，如果样本属于类别k，那么这个类别所对应的的输出节点的输出值应该为1，其他节点的输出都为0

    例如：[0,0,0,0,0,0,0,1,0,0]

    那么神经网络的输出结果越接近[0,0,0,0,0,0,0,1,0,0]越好

如何判断一个输出向量和期望的向量有多接近呢？这就用到了交叉熵

（2）交叉熵

交叉熵是刻画两个概率分布之间的距离，也是分类问题中使用比较广泛的一种损失函数

给定两个概率分布p和q,通过q来表示p的交叉熵：

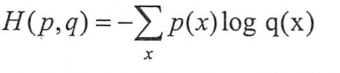
该公式表示通过概率分布q来表达概率分布p的困难程度（p代表的正确答案，q代表的是预测值）概率分布p(X=x)满足：

但是神经网络的输出不一定是一个概率分布，所以需要在神经网络的输出层添加一个Softmax层（即Softmax回归）

Softmax模型可以用来给不同的对象分配概率

假设原始的神经网络输出为y1,y2……yn，那么经过Softmax回归处理之后的输出为：

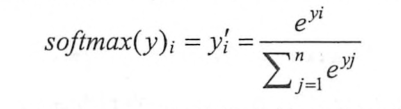
Softmax举例

交叉熵举例：

交叉熵刻画的是两个概率分布的距离，即交叉熵的值越小，两个概率分布越接近。

假设有一个三分类问题：

    某个样例的正确答案是（1,0,0）

    某模型经过Softmax回归之后的预测答案是（0.5,0.4,0.1）

    则这个预测和正确答案之间的交叉熵为：

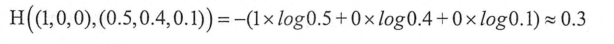
另外一个模型的预测答案是（0.8,0.1,0.1）

    则预测值和真实值之间的交叉熵为：

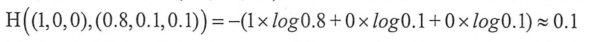
4、BP神经网络的反向传播

（1）梯度下降算法

主要用于优化单个参数的取值

举例：

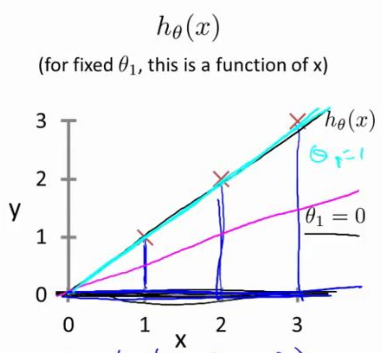
如下图：X轴表示参数θ的取值；Y轴表示损失函数J(θ)的值

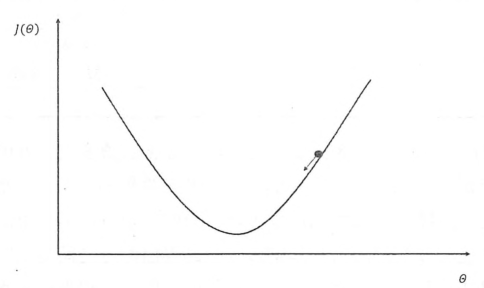
参数更新公式：

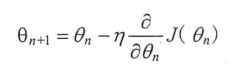
例如损失函数为J(X)=x² ,学习率为0.3

（2）反向传播算法

在所有的参数上使用梯度下降算法，从而使神经网络模型在训练数据集上的损失函数达到一个较小的值

反向传播算法是训练神经网络模型的核心算法，它可以根据定义好的损失函数优化神经网络中参数的取值

神经网络中一般选用批量梯度下降算法

5、BP神经网络优化过程总结

（1）定义神经网络的结构，通过前向传播算法计算得到预测值

（2）定义损失函数，计算预测值和真实值两者之间的差距

（3）选择反向传播优化算法，计算损失函数对每一个参数的梯度

（4）根据梯度和学习率使用梯度下降算法更新每一个参数

（5）在训练数据上反复运行反向传播优化算法，训练神经网络

BP神经网络实现MNIST手写数字识别实战：TensorFlow——MNIST手写数字识别

6、BP神经网络的进一步优化

（1）学习率（learning rate）的设置

学习率控制参数更新的速度，决定了每次参数更新的幅度。

如果学习率过大：可能导致参数在极优值的两侧来回移动。

例如：优化J(x)=x²函数，如果在优化过程中使用学习率为1

那么整个优化过程如下：

从结果可以看出：无论进行多少轮迭代，参数将在-5和5之间摇摆，而不会收敛到一个极小值

如果学习率过小，虽然能保证收敛性，但是会大大降低优化速度。

所以学习率既不能过大，也不能过小

TensorFlow中提供了一种更加灵活的学习率设置方法——指数衰减法

（指数衰减法可以先使用较大的学习率来快速得到一个比较优的解，然后随着迭代的继续逐步减小学习率，使得模型在训练后期更加稳定）

（2）过拟合问题

• 增加数据集
• 正则化方法

    正则化的思想：在损失函数中加入刻画模型复杂程度的指标

    假设用于刻画模型在训练数据上表现的损失函数为J(θ)，那么在优化时不是直接优化J(θ)，而是优化J(θ)+ λR(w)（其中R(w)刻画的模型的复杂度，而λ表示模型复杂损失在总损失中的比例）

注意：这里的θ表示的是一个神经网络中的所有参数，它包括边上的权重w和偏置项b,一般来说模型复杂度只由权重w决定

常用刻画模型复杂度的函数R(w)有两种:

一种是L1正则化，计算公式如下：

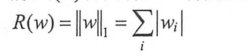
一种是L2正则化，计算公式如下：

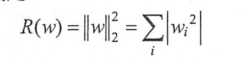
两种正则化方式的基本思想：通过限制权重大小，使模型不能任意拟合训练数据中的随机噪音

在实践中也可以将L1正则化和L2正则化同时使用，如下公式：

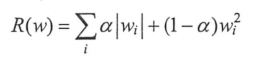
Dropout方法

dropout并不会修改代价函数而是修改深度网络本身

dropout是指在深度学习网络的训练过程中，对于神经网络单元，按照一定的概率将其暂时从网络中丢弃

（3）多层网络解决异或运算

异或运算直观来说就是如果两个输入的符号相同时（同时为正或同时为负），则输出为0，否则（一个正一个负）输出为1

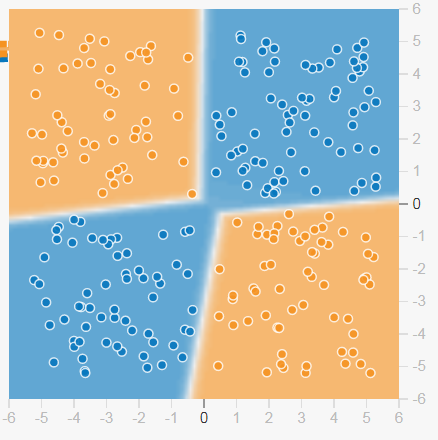
深层神经网络有组合特征提取的功能，这个特性对于解决不易提取特征向量的问题（比如图片识别、语音识别等）有很大帮助。

参考书籍：《TensorFlow实战 Google深度学习框架》

吴恩达机器学习教程

神经网络游乐场

最后

以上就是畅快悟空为你收集整理的BP神经网络的全部内容，希望文章能够帮你解决BP神经网络所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。