机器学习数学基础之python矩阵运算

一、 在Jupyter中进行Python矩阵基本运算

实验环境：

Anaconda + python3.7 + jupyter

1.python矩阵基本操作

• 矩阵的加减，行列转换
  代码如下：

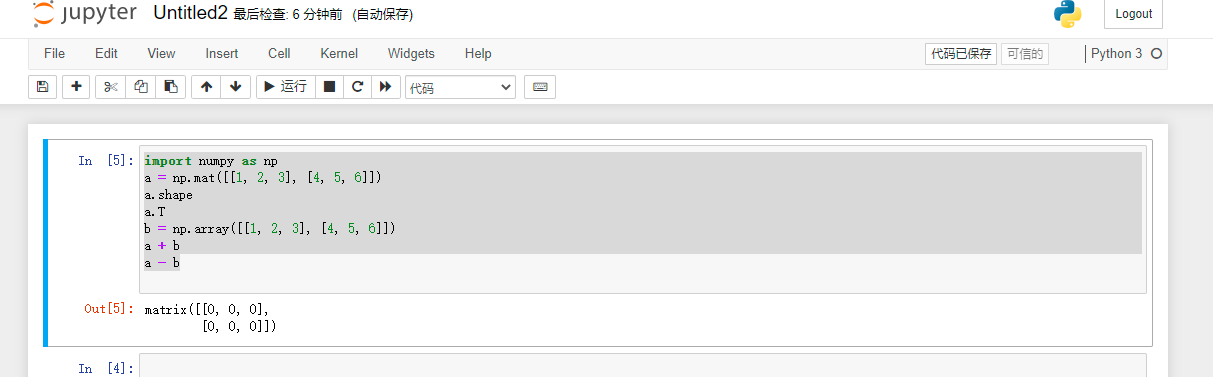
import numpy as np
a = np.mat([[1, 2, 3], [4, 5, 6]])
a.shape
a.T
b = np.array([[1, 2, 3], [4, 5, 6]])
a + b
a - b

2.python矩阵乘法

注：

矩阵之间的相乘和数的相乘不一样。

• 1.实现数乘

A = np.array([[1, 2, 3], [4, 5, 6]])
B = A.T
2 * A

结果如下：

• 2.矩阵相乘
  完整代码如下：

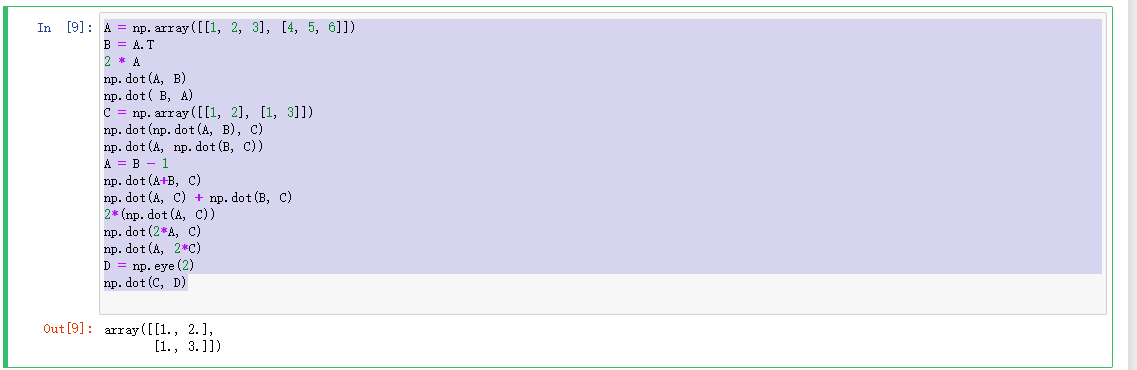
A = np.array([[1, 2, 3], [4, 5, 6]])
B = A.T
2 * A
np.dot(A, B)
np.dot( B, A)
C = np.array([[1, 2], [1, 3]])
np.dot(np.dot(A, B), C)
np.dot(A, np.dot(B, C))
A = B - 1
np.dot(A+B, C)
np.dot(A, C) + np.dot(B, C)
2*(np.dot(A, C))
np.dot(2*A, C)
np.dot(A, 2*C)
D = np.eye(2)
np.dot(C, D)

结果如下：

3.矩阵转置

注：

矩阵的转置就是行列转换。行->列

• 矩阵转置的转置就是本身：

import numpy as np

A = np.array([[1, 2, 3], [4, 5, 6]])

A.T.T

如图所示：

• 矩阵转置运算之后求和
  代码如下：

import numpy as np

A = np.array([[1, 2, 3], [4, 5, 6]])

A.T.T
B = A.T
C = B - 1
(B + C).T
B.T + C.T
(2 * A).T
2 * A.T
np.dot(A, B).T
np.dot(B.T, A.T)

结果如下：

4.求解矩阵的迹

• 验证方阵的迹等于方阵的转置的迹
  代码：

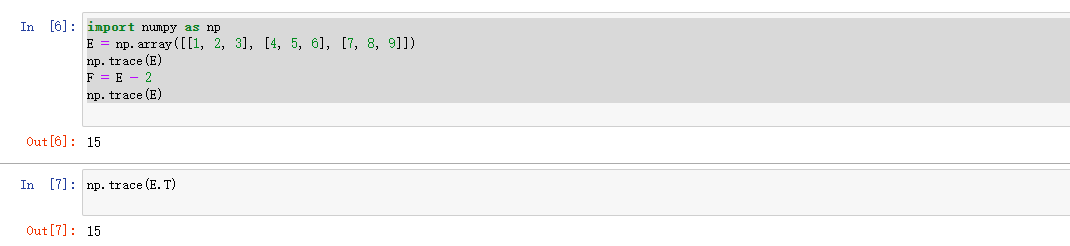
import numpy as np
E = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
np.trace(E)
F = E - 2
np.trace(E)

结果展示：

• 方阵乘积的迹
  代码：

np.trace(np.dot(E, F))
np.trace(np.dot(F, E))

结果展示：

5.方阵的行列式计算

代码如下：

E = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
F = np.array([[1, 2], [1, 3]])
np.linalg.det(E)
np.linalg.det(F)

结果展示：

6.矩阵的逆矩阵/伴随矩阵

逆矩阵的定义：

设A是数域上的一个n阶方阵，若在相同数域上存在另一个n阶矩阵B，使得： AB=BA=E。 则我们称B是A的逆矩阵，而A则被称为可逆矩阵。当矩阵A的行列式|A|不等于0时才存在可逆矩阵。

代码如下：

A = np.array([[1, -2, 1], [0, 2, -1], [1, 1, -2]])
B = np.linalg.inv(A)
A_abs = np.linalg.det(A)
B = np.linalg.inv(A)
A_bansui = B * A_abs

7.求解多元一次方程组

代码如下：

a = [[1, 2, 1], [2, -1, 3], [3, 1, 2]]
a = np.array(a)
b = [7, 7, 18]
b = np.array(b)
x = np.linalg.solve(a, b)
np.dot(a, x)

结果展示：

二、梯度下降法

1.相关概念的介绍

• 1.微分在数学中的定义：

由函数B=f(A)，得到A、B两个数集，在A中当dx靠近自己时，函数在dx处的极限叫作函数在dx处的微分，微分的中心思想是无穷分割。

• 2.梯度的定义

梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）

• 3.什么是梯度下降法

在机器学习算法中，对于很多监督学习模型，需要对原始的模型构建损失函数，接下来便是通过优化算法对损失函数进行优化，以便寻找到最优的参数。在求解机器学习参数的优化算法中，使用较多的是基于梯度下降的优化算法(Gradient Descent, GD)。

2.用梯度下降法手工求解

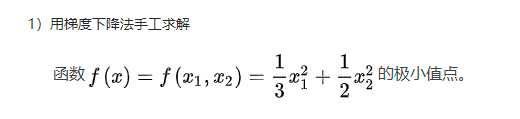
3.Excel利用梯度下降法求解近似根

• 1.初始设定
  

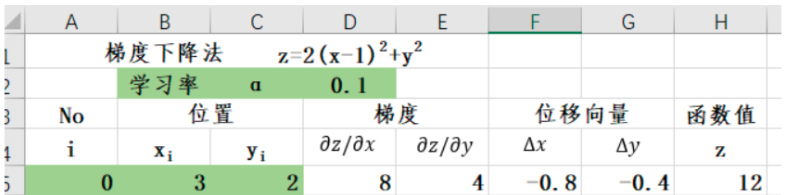
• 2.计算位移量
  

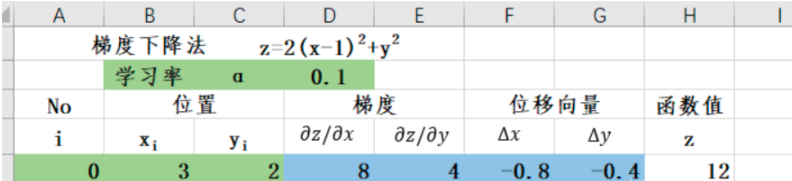
• 3.更新位置

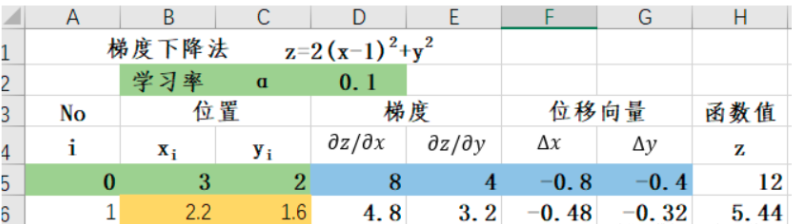
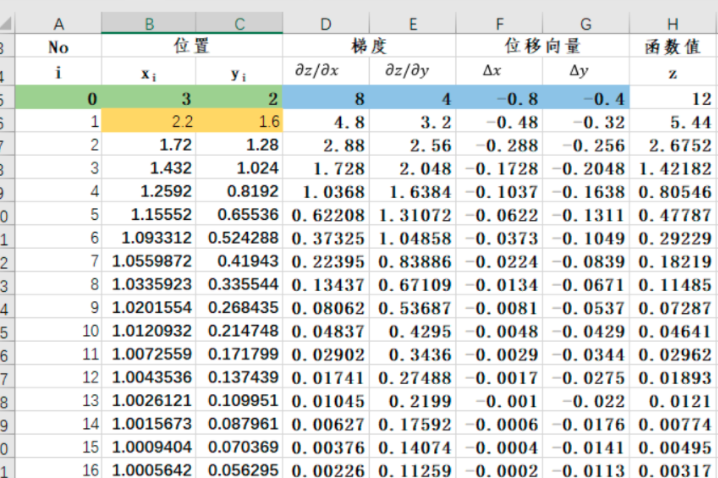
结论：函数z 在 (1,0) 处取得最小值 0

4.python编程实现求解

• 1.导入所需的库
  代码：

# 导入所需库
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import math
from mpl_toolkits.mplot3d import Axes3D
import warnings

• 2.定义相关函数

# 原函数
def Z(x,y):
    return 2*(x-1)**2 + y**2
# x方向上的梯度
def dx(x):
    return 4*x-4
# y方向上的梯度
def dy(y):
    return 2*y

• 3.重复迭代

# 初始值
X = x_0 = 3
Y = y_0 = 2
# 学习率
alpha = 0.1
# 保存梯度下降所经过的点
globalX = [x_0]
globalY = [y_0]
globalZ = [Z(x_0,y_0)]
# 迭代30次
for i in range(30):
    temX = X - alpha * dx(X)
    temY = Y - alpha * dy(Y)
    temZ = Z(temX, temY)
    # X,Y 重新赋值
    X = temX
    Y = temY
    # 将新值存储起来
    globalX.append(temX)
    globalY.append(temY)
    globalZ.append(temZ)

• 4.打印结果

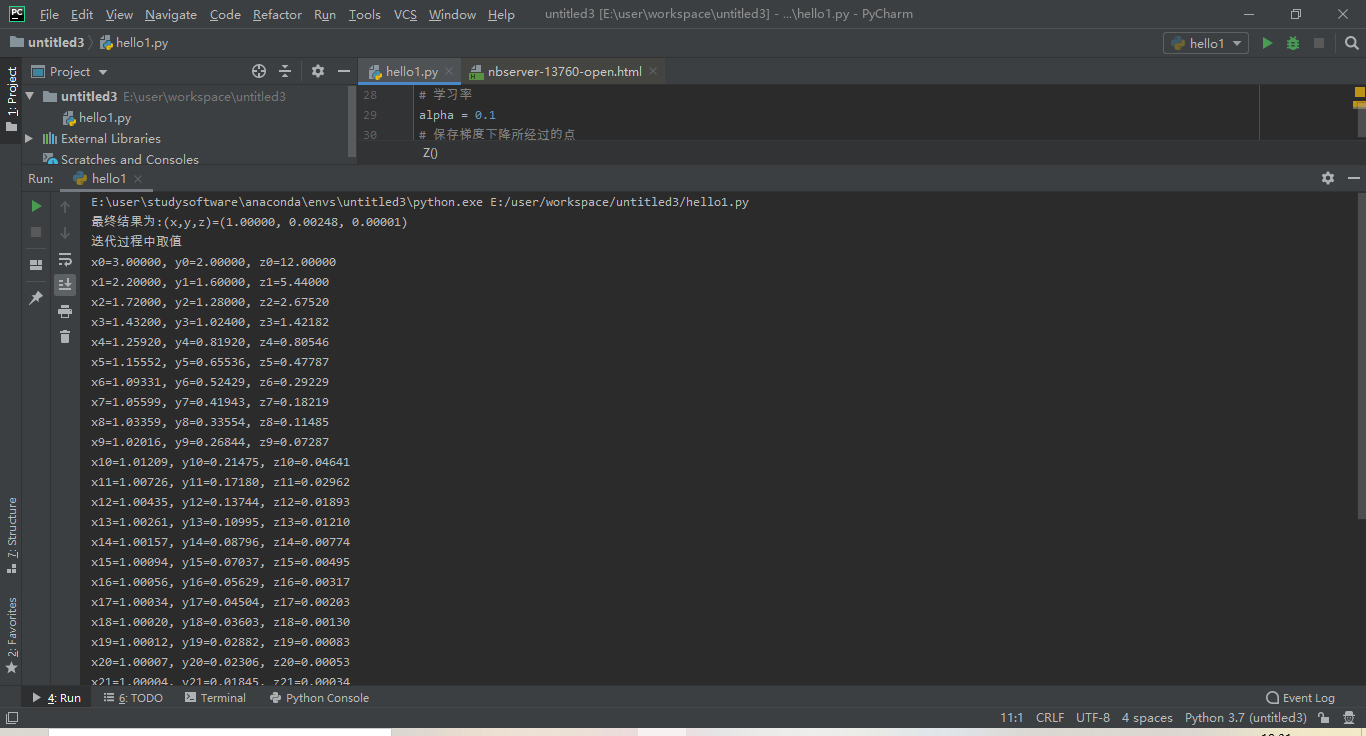
# 打印结果
print(u"最终结果为:(x,y,z)=(%.5f, %.5f, %.5f)" % (X, Y, Z(X,Y)))
print(u"迭代过程中取值")
num = len(globalX)
for i in range(num):
    print(u"x%d=%.5f, y%d=%.5f, z%d=%.5f" % (i,globalX[i],i,globalY[i],i,globalZ[i]))

结果展示：

• 5.绘制过程图

%matplotlib inline
axisX = np.arange(-4,4,0.2)
axisY = np.arange(-4,4,0.2)
axisX, axisY = np.meshgrid(axisX, axisY) # 生成xv、yv，将axisX、axisY变成n*m的矩阵，方便后面绘图
valueZ = np.array(list(map(lambda t : Z(t[0],t[1]),zip(axisX.flatten(),axisY.flatten()))))
valueZ.shape = axisX.shape # 1600的Z图还原成原来的（40,40）
%matplotlib inline

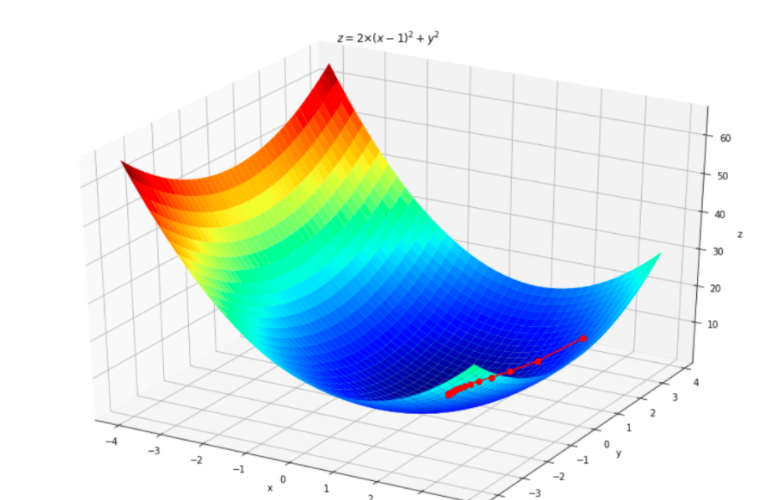
#作图
fig = plt.figure(facecolor='w',figsize=(12,8))
ax = Axes3D(fig)
ax.plot_surface(axisX,axisY,valueZ,rstride=1,cstride=1,cmap=plt.cm.jet)
ax.plot(globalX,globalY,globalZ,'ko-')
ax.set_title(u'$ z=2×(x-1)^2 + y^2  $')
ax.set_xlabel(u'x')
ax.set_ylabel(u'y')
ax.set_zlabel('z')
plt.show()

结果如图：

三、参考链接

梯度下降法

最后

以上就是虚心方盒为你收集整理的机器学习数学基础之python矩阵运算的全部内容，希望文章能够帮你解决机器学习数学基础之python矩阵运算所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。