武汉地铁站点最短路径搜索的实现（一）——Dijkstra算法（资料收集）

Dijkstra算法

1.定义概览

Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。Dijkstra算法是很有代表性的最短路径算法，在很多专业课程中都作为基本内容有详细的介绍，如数据结构，图论，运筹学等等。注意该算法要求图中不存在负权边。

问题描述：在无向图 G=(V,E) 中，假设每条边 E[i] 的长度为 w[i]，找到由顶点 V0 到其余各点的最短路径。（单源最短路径）

最短路径算法主要有二（Dijkstra算法和Floyd算法），Dijkstra算法研究的是从初始点到其他每一结点的最短路径 ，而Floyd算法研究的是任意两结点之间的最短路径

 Dijkstra算法在应对数据规模量级的增大的情况下表现出来的性能是很优越的(耗时短)，这也是在面对大规模图结构的时候不能使用Floyd算法的原因。

 

2.算法描述

1)算法思想：

Dijkstra算法是典型最短路径算法，用于计算一个节点到其他所有节点的最短路径。以源点为中心向外层层扩展，直到扩展到终点为止；算法中引入两个集合S（dis数组）和U。S的作用是记录已求出最短路径的节点(以及相应的最短路径长度即源点到该节点的最短距离)，而U则是记录还未求出最短路径的节点(以及该节点到源点s的距离)。

设G=(V,E)是一个加权有向图，把图中节点集合V分成两组，第一组点集合S包含已求出最短路径的节点（初始时S中只有初始源点s，以后每求得一条最短路径 , 就将加入到集合S中，直到全部节点都加入到S中，算法就结束了），第二组为其余未确定最短路径的节点集合（用U表示），按最短路径长度的递增次序依次把第二组的节点加入S中。在加入的过程中，总保持从源点s到S中各节点的最短路径长度不大于从源点v到U中任何节点的最短路径长度。此外，每个节点对应一个距离，S中的节点的距离就是从s到此节点的最短路径长度，U中的节点的距离，是从s到此节点只包括S中的节点为中间节点的当前最短路径长度。

2)算法步骤：

a.初始时，S只包含源点，即S＝{s}，s的距离为0。U包含除s外的其他节点，即:U={其余节点}，若s与U中节点u邻接，则<s,u>正常有权值，若u不是v的出边邻接点，则<s,u>权值为∞。

b.从U中选取一个距离s最小的节点k，把k，加入S中（该选定的距离就是v到k的最短路径长度）。

c.以k为新考虑的中间点，修改U中各节点的距离；若从源点s到节点u的距离（经过节点k）比原来距离（不经过节点k）短，则修改节点u的距离值，修改后的距离值为节点k的距离值+<k,u>边上的权。

d.重复步骤b和c直到所有节点都包含在S中。

 

 

3.算法示例

1）示例一

算法步骤：

（1）初始时，源点 s 的路径权重被赋为 0 （dis[s] = 0）。若对于节点 s 存在能直接到达的边（s,m），则把dis[m]设为w（s, m）,同时把所有其他（s不能直接到达的）节点的路径长度设为无穷大。初始时，集合S只有节点s；

（2）然后，从dis数组选择最小值，则该值就是源点s到该值对应的节点的最短路径，并且把该点加入到集合S中，此时完成一个节点；

（3）再然后，需要看新加入的节点是否可以到达其他节点并且看通过该节点到达其他点的路径长度是否比源点直接到达短，如果是，那么就替换这些顶点在dis中的值；

（4）从dis中找出最小值，重复上述动作，直到S中包含了图的所有节点。

图Y1及其邻接矩阵D：
                                                              

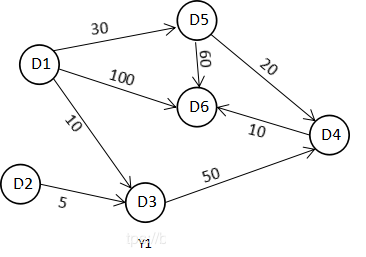
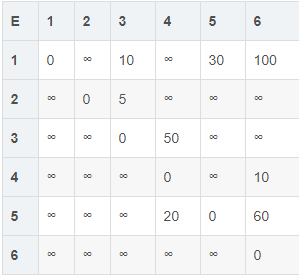
迪杰斯特拉进行算法演示(以顶点D1为起点)：

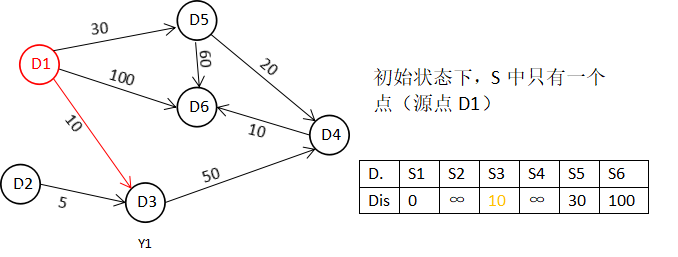
step1：S={D1}，Dis以节点D1到U中的节点距离赋值

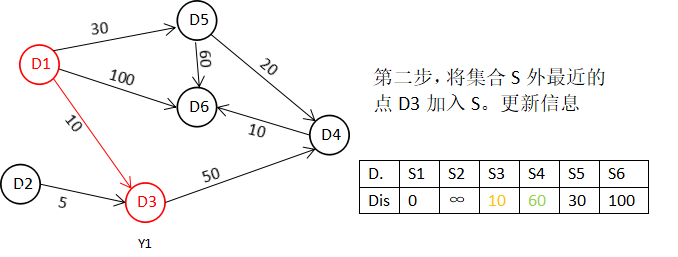
step2：在数组 Dis中除S={D1}对应的Dis[0]（D.s1）外，搜索到最小值D.s3，当前离D1节点最近是 D3节点。搜索D3 节点后，Dis[2]（下标从0开始）的值就已经从“估计值”变为了“确定值”。确定最短路径D1-D3：10，S={D1，D3}

step3：有新的顶点D3进入集合S，发现D3为弧尾的有： < D3,D4 >,那么我们看看路径：D1–D3–D4的长度是否比D1–D4短，因为Dis[3]代表的就是D1–D4的长度为无穷大，而D1–D3–D4的长度为：10+50=60，(Dis[2]+w<D3,D4>=10+50=60)<Dis[3]，所以更新Dis[3]的值。

搜索D3的邻接点Di（Di∉S），D.si=min{D.s3+w(D3，Di),D.si}。

step4：我们从除dis[2]和dis[0]外的其他值中寻找最小值，发现dis[4]的值最小，通过之前是解释的原理，可以知道D1到D5的最短距离就是dis[4]的值，然后，我们把D5加入到集合S中，然后，考虑D5的出度是否会影响我们的数组dis的值，D5有两条出度：< D5,D4>和 < D5,D6>,然后我们发现：D1–D5–D4的长度为：50，而dis[3]的值为60，所以我们要更新dis[3]的值.另外，D1-D5-D6的长度为：90，而dis[5]为100，所以我们需要更新dis[5]的值。

在数组 Dis中除S={D1，D3}对应的D.s1、D.s3外，搜索到最小值D.s5=30，确定最短路径D1-D5：30，S={D1，D3，D5}。搜索D5的邻接点得：D6、D4，修改D.s6=min{ D.s5+w<D5,D6>=30+60=90，D.s6=100}=90，D.s4=min{D.s5+w<D5,D4>=30+20=50，D.s4=60}=50。

 

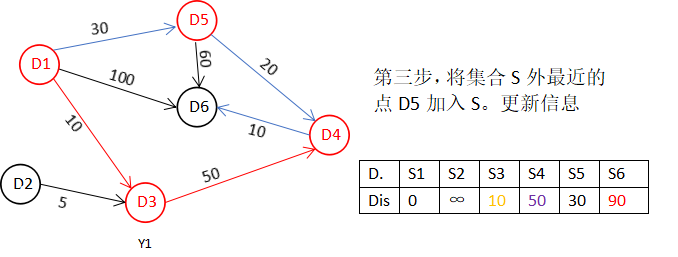
step5：继续从dis中选择未确定的顶点的值中选择一个最小的值，发现dis[3]的值是最小的，所以把D4加入到集合S中。此时集合S={D1,D3,D5,D4},然后，考虑D4的出度是否会影响我们的数组dis的值，D4有一条出度：< D4,D6>,然后我们发现：D1–D5–D4–D6的长度为：60，而dis[5]的值为90，所以我们要更新dis[5]的值。

在数组 Dis中除S={D1，D3，D5}对应的D.s1、D.s3、D.s5外，搜索到最小值D.s4=50，确定最短路径D1-D4：50，S={D1，D3，D5，D4}。搜索D4的邻接点得：D6，修改D.s6=min{ D.s4+w<D4,D6>=50+10=60，D.s6=90}=60。

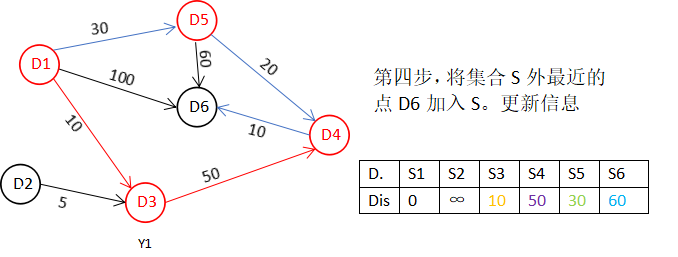
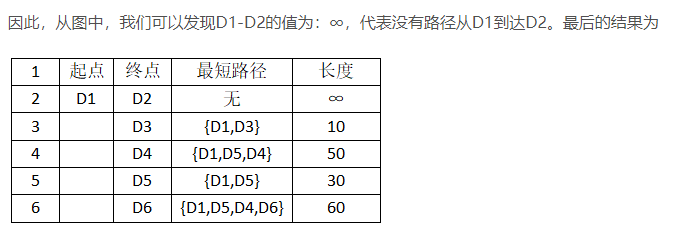
然后，我们使用同样原理，分别确定了D6和D2的最短路径，最后dis的数组的值如下：

                                            

2）示例二

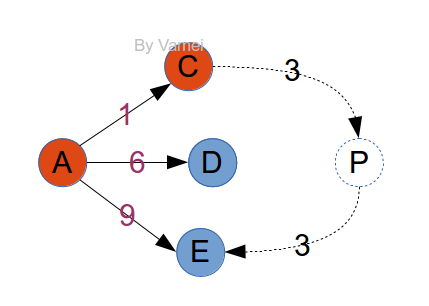
将节点分为三种：已知点：已知到达A最短距离的点；邻接点：有从记录点出发的边，直接相邻的点； 未知点。

最初的已知点只有A。已知点的直接下游节点为邻接点。对于邻接点，我们需要独立的记录它们。我们要记录的有：

· 当前情况下，从A点出发到达该邻接点的最短距离。比如对于上面的点D，为6。

· 此最短距离下的上游节点。对于上面的点D来说，为A。

每次，我们将邻接点中最短距离最小的点X转为已知点，并将该点的直接下游节点Q，改为邻接点。我们需要计算从A出发，经由X，到达这些新增邻接点Q的距离：新距离 = X最短距离 + QX边的权重。此时有两种情况，

· 如果下游节点Q还不是邻接点，那么直接加入，Q最短距离 = 新距离，Q上游节点为X。

· 如果下游节点Q已经是邻接点，记录在册的上游节点为Y，最短距离为y。如果新距离小于y，那么最小距离改为新距离，上游节点也改为X。否则保持原记录不变。

我们还用上面的图，探索A到E的路径：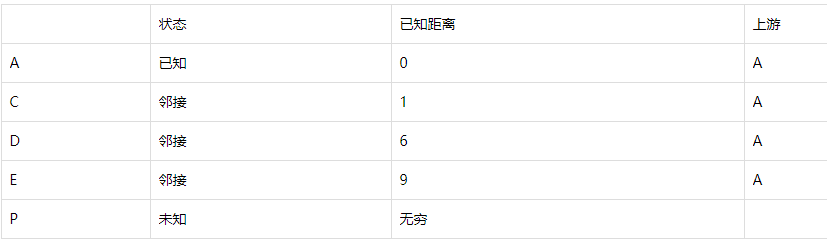

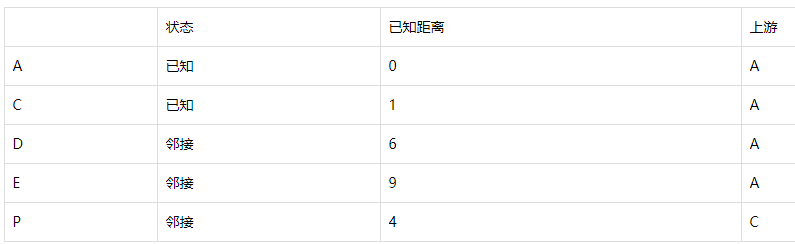
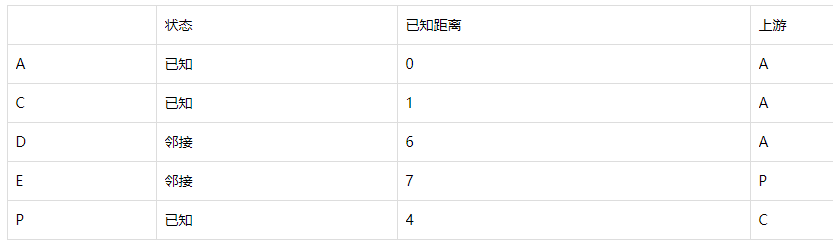
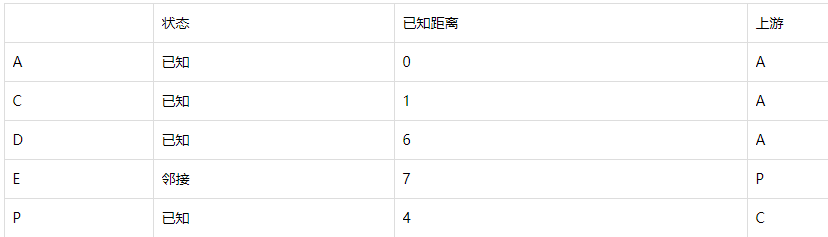
最后，E成为已知。倒退，可以知道路径为E, P, C, A。正过来，就是从A到E的最短路径了。

 2）示例三

 

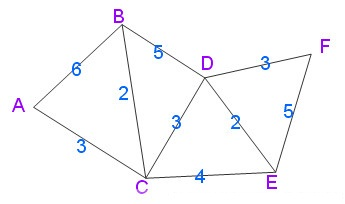
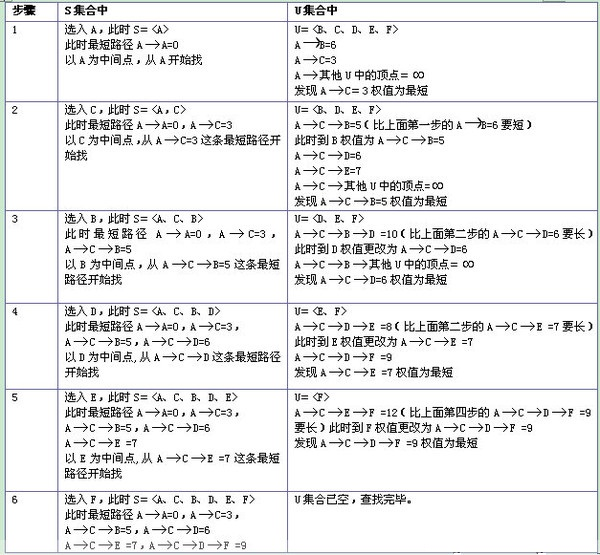
用Dijkstra算法找出以A为起点的单源最短路径步骤如下

 

Floyd算法

1.定义概览

Floyd-Warshall算法（Floyd-Warshall algorithm）是解决任意两点间的最短路径的一种算法，可以正确处理有向图或负权的最短路径问题，同时也被用于计算有向图的传递闭包。Floyd-Warshall算法的时间复杂度为O(N³)，空间复杂度为O(N²)。

 

2.算法描述

1)算法思想原理：

     Floyd算法是一个经典的动态规划算法。用通俗的语言来描述的话，首先我们的目标是寻找从点i到点j的最短路径。从动态规划的角度看问题，我们需要为这个目标重新做一个诠释（这个诠释正是动态规划最富创造力的精华所在）

      从任意节点i到任意节点j的最短路径不外乎2种可能，1是直接从i到j，2是从i经过若干个节点k到j。所以，我们假设Dis(i,j)为节点u到节点v的最短路径的距离，对于每一个节点k，我们检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立，如果成立，证明从i到k再到j的路径比i直接到j的路径短，我们便设置Dis(i,j) = Dis(i,k) + Dis(k,j)，这样一来，当我们遍历完所有节点k，Dis(i,j)中记录的便是i到j的最短路径的距离。

2).算法描述：

a.从任意一条单边路径开始。所有两点之间的距离是边的权，如果两点之间没有边相连，则权为无穷大。 　　

b.对于每一对顶点 u 和 v，看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比己知的路径更短。如果是更新它。

3).Floyd算法过程矩阵的计算----十字交叉法

方法：两条线，从左上角开始计算一直到右下角 如下所示

给出矩阵，其中矩阵A是邻接矩阵，而矩阵Path记录u,v两点之间最短路径所必须经过的点

相应计算方法如下：

最后A₃即为所求结果

 

3.算法代码实现

typedef struct
{

char vertex[VertexNum];
//顶点表


int edges[VertexNum][VertexNum];
//邻接矩阵,可看做边表


int n,e;
//图中当前的顶点数和边数

}MGraph;

void Floyd(MGraph g)
{

　　int A[MAXV][MAXV];

　　int path[MAXV][MAXV];

　　int i,j,k,n=g.n;

　　for(i=0;i<n;i++)

　　for(j=0;j<n;j++)

　　{ 　　

A[i][j]=g.edges[i][j];

　　 path[i][j]=-1;

　 }

　　for(k=0;k<n;k++)
 　　{

　　for(i=0;i<n;i++)

　　for(j=0;j<n;j++)

　　if(A[i][j]>(A[i][k]+A[k][j]))

　　{

　　A[i][j]=A[i][k]+A[k][j];

　　path[i][j]=k;

　 }

　}
}