视觉里程计- 位姿

50 阅读 0 评论 33 点赞

我是靠谱客的博主健忘缘分，最近开发中收集的这篇文章主要介绍视觉里程计- 位姿，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

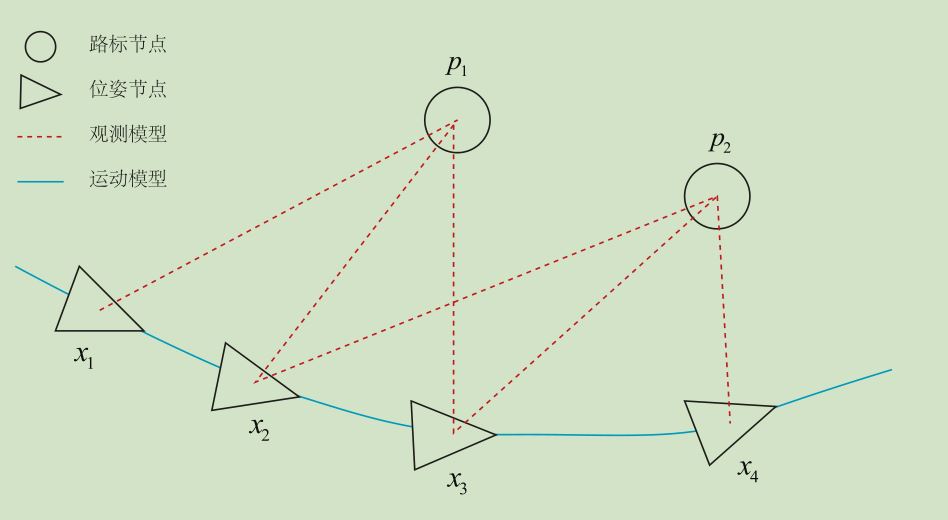
注意到位姿节点之间的变换并不是位姿，之前一直有误解；

一般地；

路标节点：也就是观测方程【数学形式下见】的观测值，也就是特征点的像素坐标[u,v],或者该帧相机坐标系下的3d坐标[x,y,z];

位姿节点：也就是运动方程【数学形式下见】的输出值。例如：上述x1、x2、x3、X4对应位姿为：Tcw1、Tcw2、Tcw3、Tcw4。这里的Tcw表示对应帧相机坐标系->世界坐标系的变换；比如：在x1处看到了路标点p1，在x2处也看到了路标点p1（当然是通过特征匹配才知道再次看到）考虑以下两种情况：

1> x1对应第一帧，x2对应第二帧

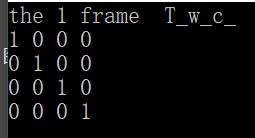
那么x1的相机坐标系即为：世界坐标系；那么第一帧位姿我们直接初始化为：

第二帧我们要：通过……solvePNPransac(points3d_1, points2d_2,R,t);来求解，points3d_1对应的是世界坐标系下的3D点（在这种情形，第一帧相机坐标系也就是世界坐标系，所以第一帧相机坐标系下的3D点）, points2d_2是第二帧像素点（设第二帧对应3D路标点（在第二帧相机坐标系下）为：points3d_2）。

在这里[左乘]，

Tcw2 * points3d_1 = points3d_2

同时必须知道：（假设两帧之间的变换 T12，也就是位姿变换）

T12 * Tcw1 = Tcw2

2> x2对应第2帧，x3对应第3帧

接着，我们再次想通过solvePNPransac(points3d_2_, points2d_3,R,t)来求解Tcw3，points3d_2_ （世界坐标系）肯定不是 points3d_2(相机坐标系)，所以在第一种情形你就应该提前将points3d_2 从它所在的相机坐标系映射到世界坐标系，故：

points3d_2_ = Tcw2.inverse() * points3d_2

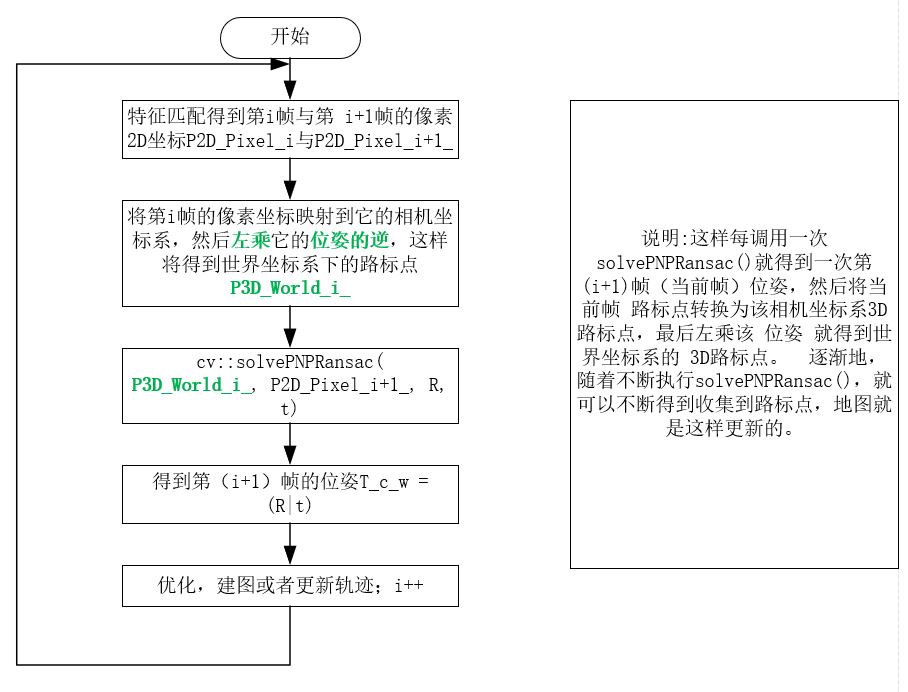
我们得出流程图如下图：

观测模型：具体见下

运动模型：具体见下

两个模型与G2O结合了解说明；

位姿：位置和姿态；

对于上述位姿图，我们假设 x1 对应参考帧 ref_（同时假设是第一帧），x2对应当前帧curr_（同时假设是第二帧）;我们通过......最后通过opencv中API solvePNPransac();求出的R|t 其实是Tcw；

Tcw指的是：当前帧与世界坐标系之间的变换；

Trw指的是：参考帧与世界坐标系之间的变换。那么待估计的两帧之间的变换为：Tcr，构成左乘关系：

Tcr， s.t. Tcr * Trw = Tcw

P_camera_curr 指的是：当前帧3D路标点（相机坐标系）

P_world_ref 指的是：参考帧3D路标点 (世界坐标系）

P_camera_curr = Tcw*P_world_ref

这里 opencv中的 solvePNPransac 求出来的是 T = （R|t）；依据上述公式：所以你要将当前帧3D路标点转化到世界坐标系，应该是左乘：Tcw.inverse() * P_camera_curr = P_world_ref;请看以下代码【就是匹配，第一帧相机坐标系当作世界坐标系，第二帧就是相机坐标系，重点关注代码 81行 - 124行】：


1 #include <iostream>

2 #include <opencv2/core/core.hpp>

3 #include <opencv2/features2d/features2d.hpp>

4 #include <opencv2/highgui/highgui.hpp>

5 #include <opencv2/calib3d/calib3d.hpp>

6 #include <Eigen/Core>

7 #include <Eigen/Geometry>

8 #include <g2o/core/base_vertex.h>

9 #include <g2o/core/base_unary_edge.h>
 10 #include <g2o/core/block_solver.h>
 11 #include <g2o/core/optimization_algorithm_levenberg.h>
 12 #include <g2o/solvers/csparse/linear_solver_csparse.h>
 13 #include <g2o/types/sba/types_six_dof_expmap.h>
 14 #include <chrono>
 15
 16 using namespace std;
 17 using namespace cv;
 18
 19 #include"sophusse3.h"
 20 #include"sophusso3.h"
 21
 22 void find_feature_matches(
 23
const Mat& img_1, const Mat& img_2,
 24
std::vector<KeyPoint>& keypoints_1,
 25
std::vector<KeyPoint>& keypoints_2,
 26
std::vector< DMatch >& matches);
 27
 28 // 像素坐标转相机归一化坐标
 29 Point2d pixel2cam(const Point2d& p, const Mat& K);
 30
 31 void bundleAdjustment(
 32 const vector<Point3f> points_3d,
 33 const vector<Point2f> points_2d,
 34 const Mat& K,
 35 Mat& R, Mat& t
 36 );
 37
 38 int main()
 39 {
 40
//-- 读取图像
 41
Mat img_1 = imread("color/b.png", CV_LOAD_IMAGE_COLOR);
 42
Mat img_2 = imread("color/c.png", CV_LOAD_IMAGE_COLOR);
 43
 44
vector<KeyPoint> keypoints_1, keypoints_2;
 45
vector<DMatch> matches;
 46 
find_feature_matches(img_1, img_2, keypoints_1, keypoints_2, matches);
 47
cout << "一共找到了" << matches.size() << "组匹配点" << endl;
 48
 49
// 建立3D点
 50
Mat depth_1 = imread("depth/b.pgm", CV_LOAD_IMAGE_UNCHANGED);
// 深度图为16位无符号数，单通道图像
 51
Mat depth_2 = imread("depth/c.pgm", CV_LOAD_IMAGE_UNCHANGED);
// 深度图为16位无符号数，单通道图像
 52
//Mat K = (Mat_<double>(3, 3) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1);
 53
Mat K = (Mat_<double>(3, 3) << 518.0, 0, 325.5, 0, 519.0, 253.5, 0, 0, 1);
 54
vector<Point3f> pts_3d1;//世界坐标点
 55
vector<Point3f> pts_3d2;
 56
vector<Point2f> pts_2d;//相机坐标系点（归一化？？？）
 57
//【注：】这里表示同一个3D点在两幅图中的图二对应像素点，本来就是求世界坐标系下的r、t
 58
for (DMatch m : matches)
 59 
{
 60
//取出深度值，此时彩图和深度图已经对齐
 61
ushort d1 = depth_1.ptr<unsigned short>(int(keypoints_1[m.queryIdx].pt.y))[int(keypoints_1[m.queryIdx].pt.x)];
 62
ushort d2 = depth_2.ptr<unsigned short>(int(keypoints_2[m.trainIdx].pt.y))[int(keypoints_2[m.trainIdx].pt.x)];
 63
if ((d1 == 0) || (d2 == 0))
// bad depth
 64
continue;
 65
float dd1 = d1 / 1.0;
 66
float dd2 = d2 / 1.0;
 67
Point2d p1 = pixel2cam(keypoints_1[m.queryIdx].pt, K); // 相机坐标系归一化平面：p1的形式 [x/z,y/z,1]
 68
Point2d p2 = pixel2cam(keypoints_2[m.trainIdx].pt, K);
 69
pts_3d1.push_back(Point3f(p1.x*dd1, p1.y*dd1, dd1));//乘以Z就得到形式
[x,y,z]?????左边相机为参考，把他当作世界坐标系,确实是这样的
 70
pts_3d2.push_back(Point3f(p2.x*dd2, p2.y*dd2, dd2));
 71
pts_2d.push_back(keypoints_2[m.trainIdx].pt);//图二中的2D像素坐标[u,v]
 72 
}
 73
 74
cout << "3d-2d pairs: " << pts_3d1.size() << endl;
 75
 76 
Mat r, t;
 77
// 调用OpenCV 的 PnP 求解r t，可选择EPNP，DLS等方法
 78
//solvePnP(pts_3d, pts_2d, K, Mat(), r, t, false);
 79
//solvePnP(pts_3d1, pts_2d, K, Mat(), r, t, false, SOLVEPNP_EPNP);
 80
 81
cv::solvePnPRansac(pts_3d1, pts_2d, K, Mat(), r, t, false, 100, 1.0, 0.99);
 82
 83 
Mat R;
 84
cv::Rodrigues(r, R); // r为旋转向量形式，用Rodrigues公式转换为矩阵
 85
//RR = -R.inv();
 86
cout << "R=" << endl << R << endl;
 87
cout << "t=" << endl << t << endl;
 88
//************************************************************************************************
 89
// 李群
 90
//************************************************************************************************
 91
Sophus::SE3 T_se3 = Sophus::SE3(
 92
Sophus::SO3(r.at<double>(0, 0), r.at<double>(1, 0), r.at<double>(2, 0)),
 93
Sophus::Vector3d(t.at<double>(0, 0), t.at<double>(1, 0), t.at<double>(2, 0))
 94 
);
 95
cout << "T_se3 = " << T_se3.matrix() << endl;
 96
//************************************************************************************************
 97
// 欧氏群
 98
//************************************************************************************************
 99
Eigen::Isometry3d T_Isometry3d = Eigen::Isometry3d::Identity();
100
//Eigen::AngleAxisd rot_vec(r.at<double>(0, 0), r.at<double>(1, 0), r.at<double>(2, 0));
101
Eigen::Vector3d trans(t.at<double>(0, 0), t.at<double>(1, 0), t.at<double>(2, 0));
102
Eigen::Matrix<double, 3, 3> R_;
103
R_ << R.at<double>(0,0), R.at<double>(0,1), R.at<double>(0,2),
104
R.at<double>(1,0), R.at<double>(1,1), R.at<double>(1,2),
105
R.at<double>(2,0), R.at<double>(2,1), R.at<double>(2,2);
106 
T_Isometry3d.rotate(R_);
107 
T_Isometry3d.pretranslate(trans);
108
cout << " T_Isometry3d = " << T_Isometry3d.matrix() << endl;
109
110
cout << "calling bundle adjustment" << endl;
111 
bundleAdjustment(pts_3d1, pts_2d, K, R, t);
112
//************************************************************************************************
113
// 计算误差：error = point3d_curr -( R * point3d_ref + t )
114
//************************************************************************************************
115
for (int i = 0; i < 20; i++)
116 
{
117
cout << " pts_3d1 =
" << pts_3d1[i] << endl;
118
cout << " pts_3d2 =
" << pts_3d2[i] << endl;
119
cout << " error " <<
120
(Mat_<double>(3, 1) << pts_3d2[i].x, pts_3d2[i].y, pts_3d2[i].z)
121
- R*((Mat_<double>(3, 1) << pts_3d1[i].x, pts_3d1[i].y, pts_3d1[i].z)) - t
122
<< endl;
123
cout << endl;
124 
}
125
126
waitKey(0);
127
return 0;
128 }
129
130 void find_feature_matches(const Mat& img_1, const Mat& img_2,
131
std::vector<KeyPoint>& keypoints_1,
132
std::vector<KeyPoint>& keypoints_2,
133
std::vector< DMatch >& matches)
134 {
135
//-- 初始化
136 
Mat descriptors_1, descriptors_2;
137
// used in OpenCV3
138
Ptr<FeatureDetector> detector = ORB::create(1000);
139
Ptr<DescriptorExtractor> descriptor = ORB::create();
140
// use this if you are in OpenCV2
141
// Ptr<FeatureDetector> detector = FeatureDetector::create ( "ORB" );
142
// Ptr<DescriptorExtractor> descriptor = DescriptorExtractor::create ( "ORB" );
143
Ptr<DescriptorMatcher> matcher = DescriptorMatcher::create("BruteForce-Hamming");
144
//-- 第一步:检测 Oriented FAST 角点位置
145
detector->detect(img_1, keypoints_1);
146
detector->detect(img_2, keypoints_2);
147
148
//-- 第二步:根据角点位置计算 BRIEF 描述子
149
descriptor->compute(img_1, keypoints_1, descriptors_1);
150
descriptor->compute(img_2, keypoints_2, descriptors_2);
151
152
//-- 第三步:对两幅图像中的BRIEF描述子进行匹配，使用 Hamming 距离
153
vector<DMatch> match;
154
// BFMatcher matcher ( NORM_HAMMING );
155
matcher->match(descriptors_1, descriptors_2, match);
156
157
//-- 第四步:匹配点对筛选
158
double min_dist = 10000, max_dist = 0;
159
160
//找出所有匹配之间的最小距离和最大距离, 即是最相似的和最不相似的两组点之间的距离
161
for (int i = 0; i < descriptors_1.rows; i++)
162 
{
163
double dist = match[i].distance;
164
if (dist < min_dist) min_dist = dist;
165
if (dist > max_dist) max_dist = dist;
166 
}
167
168
printf("-- Max dist : %f n", max_dist);
169
printf("-- Min dist : %f n", min_dist);
170
171
//当描述子之间的距离大于两倍的最小距离时,即认为匹配有误.但有时候最小距离会非常小,设置一个经验值30作为下限.
172
for (int i = 0; i < descriptors_1.rows; i++)
173 
{
174
if (match[i].distance <= max(2 * min_dist, 30.0))
175 
{
176 
matches.push_back(match[i]);
177 
}
178 
}
179
180
181
182 
Mat img_match;
183 
Mat img_goodmatch;
184 
drawMatches(img_1, keypoints_1, img_2, keypoints_2, match, img_match);
185 
drawMatches(img_1, keypoints_1, img_2, keypoints_2, matches, img_goodmatch);
186
namedWindow("所有匹配点对", CV_WINDOW_NORMAL);
187
imshow("所有匹配点对", img_match);
188
namedWindow("优化后匹配点对", CV_WINDOW_NORMAL);
189
imshow("优化后匹配点对", img_goodmatch);
190 }
191
192 Point2d pixel2cam(const Point2d& p, const Mat& K)// [u,v,1] - > [x/z, y/z, 1]
193 {
194
return Point2d
195 
(
196
(p.x - K.at<double>(0, 2)) / K.at<double>(0, 0),
197
(p.y - K.at<double>(1, 2)) / K.at<double>(1, 1)
198 
);
199 }
200
201
202 void bundleAdjustment(
203 const vector< Point3f > points_3d,
204 const vector< Point2f > points_2d,
205 const Mat& K,
206 Mat& R, Mat& t)
207 {
208 // 初始化g2o
209 typedef g2o::BlockSolver< g2o::BlockSolverTraits<6, 3> > Block;
// pose 维度为 6, landmark 维度为 3
210 Block::LinearSolverType* linearSolver = new g2o::LinearSolverCSparse<Block::PoseMatrixType>(); // 线性方程求解器
211 Block* solver_ptr = new Block(linearSolver);
// 矩阵块求解器
212 g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg(solver_ptr);
213 g2o::SparseOptimizer optimizer;
214 optimizer.setAlgorithm(solver);
215
216 // vertex
217 g2o::VertexSE3Expmap* pose = new g2o::VertexSE3Expmap(); // camera pose
218 Eigen::Matrix3d R_mat;
219 R_mat <<
220 R.at<double>(0, 0), R.at<double>(0, 1), R.at<double>(0, 2),
221 R.at<double>(1, 0), R.at<double>(1, 1), R.at<double>(1, 2),
222 R.at<double>(2, 0), R.at<double>(2, 1), R.at<double>(2, 2);
223 pose->setId(0);
224 pose->setEstimate(g2o::SE3Quat(
225 R_mat,
226 Eigen::Vector3d(t.at<double>(0, 0), t.at<double>(1, 0), t.at<double>(2, 0))
227 ));
228 optimizer.addVertex(pose);
229
230 int index = 1;
231 for (const Point3f p : points_3d)
// landmarks
232 {
233 g2o::VertexSBAPointXYZ* point = new g2o::VertexSBAPointXYZ();
234 point->setId(index++);
235 point->setEstimate(Eigen::Vector3d(p.x, p.y, p.z));
236 point->setMarginalized(true); // g2o 中必须设置 marg 参见第十讲内容
237 optimizer.addVertex(point);
238 }
239
240 // parameter: camera intrinsics
241 g2o::CameraParameters* camera = new g2o::CameraParameters(
242 K.at<double>(0, 0), Eigen::Vector2d(K.at<double>(0, 2), K.at<double>(1, 2)), 0
243 );
244 camera->setId(0);
245 optimizer.addParameter(camera);
246
247 // edges
248 index = 1;
249 for (const Point2f p : points_2d)
250 {
251 g2o::EdgeProjectXYZ2UV* edge = new g2o::EdgeProjectXYZ2UV();
252 edge->setId(index);
253 edge->setVertex(0, dynamic_cast<g2o::VertexSBAPointXYZ*> (optimizer.vertex(index)));
254 edge->setVertex(1, pose);
255 edge->setMeasurement(Eigen::Vector2d(p.x, p.y));
256 edge->setParameterId(0, 0);
257 edge->setInformation(Eigen::Matrix2d::Identity());
258 optimizer.addEdge(edge);
259 index++;
260 }
261
262 chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
263 optimizer.setVerbose(true);
264 optimizer.initializeOptimization();
265 optimizer.optimize(100);
266 chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
267 chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>> (t2 - t1);
268 cout << "optimization costs time: " << time_used.count() << " seconds." << endl;
269
270 cout << endl << "after optimization:" << endl;
271 cout << "T=" << endl << Eigen::Isometry3d(pose->estimate()).matrix() << endl;
272 }

View Code

这里我们只关心运动，不关心结构。换句话说，只要通过特征点成功求出了运动，我们就不再需要这帧的特征点了。这种做法当然会有缺陷，但是忽略掉数量庞大的特征点可以节省许多的计算量。然后，在 t 到 t + 1 时刻，我们又以 t 时刻为参考帧，考虑 t 到 t + 1 间的运动关系。如此往复，就得到了一条运动轨迹。