VIO中的预积分推导

为什么要预积分呢？

首先积分是肯定需要的，因为IMU的频率通常是远高于Camera的，而IMU获得的是每一时刻的加速度和角速度，我们通过积分获得两帧之间的由IMU测出的位移和旋转变换。那么预积分呢？在世界坐标系下的连续时刻积分是这样计算的：

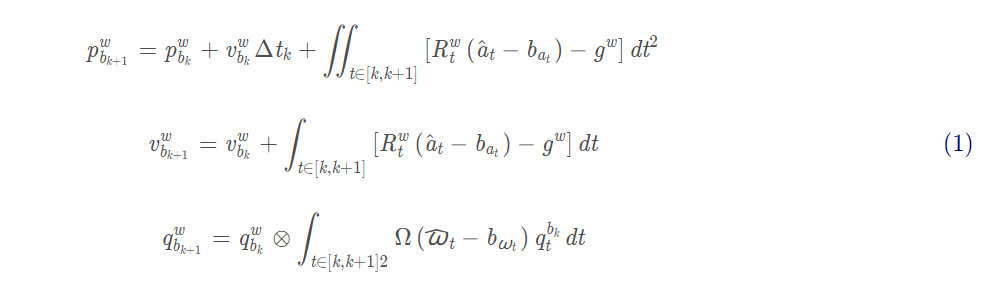
其中：

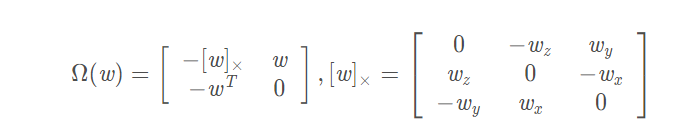
因为我们获得的IMU数据是离散的，所以第一步我们先需要对上述（1）式进行离散化

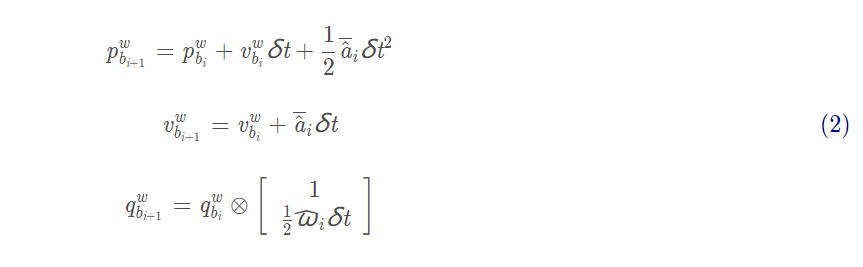
其中，运用了中值积分有

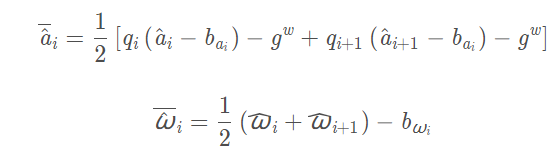
这样会遇到一个问题就是假如我们通过后端优化使得使得前一个状态改变那么这个状态又需要重新积分，如图所说：

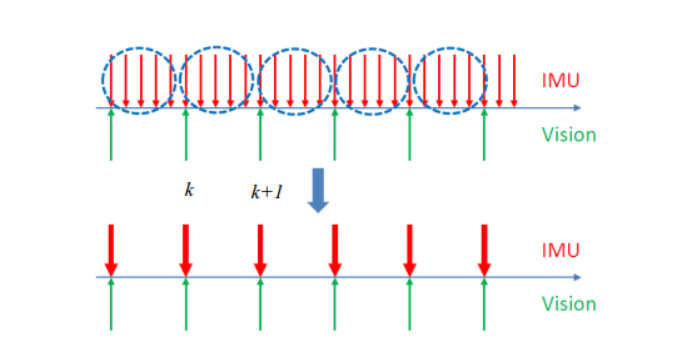
我们的后端优化里面的代价函数是包括两帧之间的残差量，以位置为例，就是状态量Pk和Pk+1以及IMU积分出来的结果之间的差，如果我们想获得这个位置差，我们如果按照（2）式计算，我们需要计算上图第一幅图中红色箭头的每一个位置的状态量，这是我们不愿意发生的，因此我们引入了预积分，它的作用就是避免重复积分，将IMU预积分的参考坐标系改为前一帧体坐标系，从而获得两帧之间的相对运动，也就是第二幅图中红色箭头之间的量。

既然我们要避免第i帧的影响，我们就需要以第i帧为参考系。简单来说就是把绝对位置，变成相对与前一帧的位置。

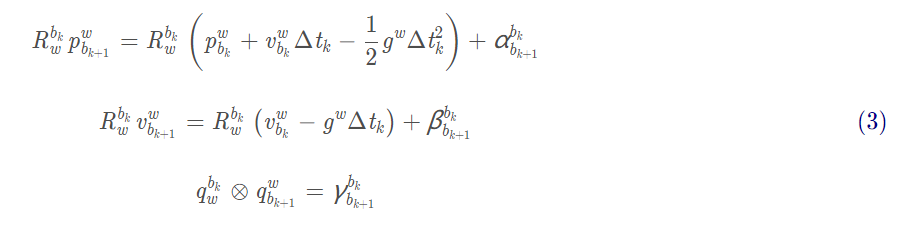
其中

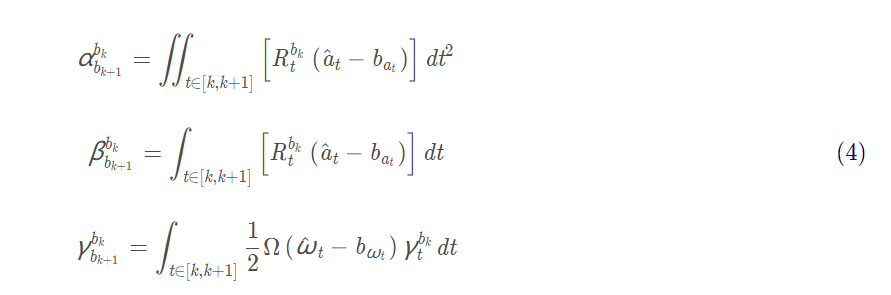
上述（4）式就是我们需要的预积分公式了，离散化后：

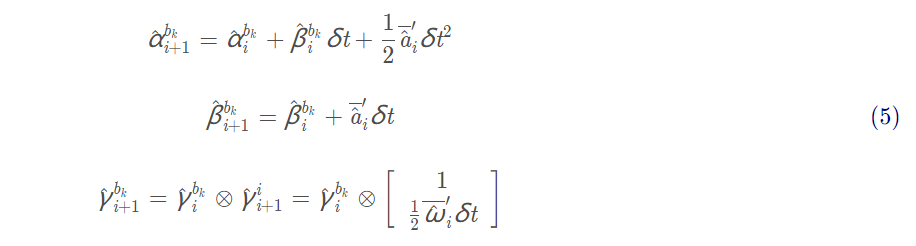
其中

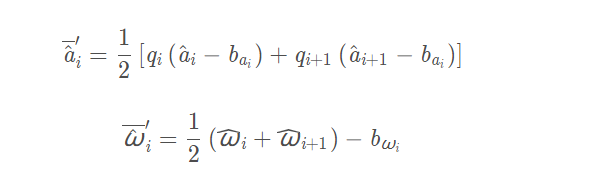
这里会存在一个Bias相关的误差：

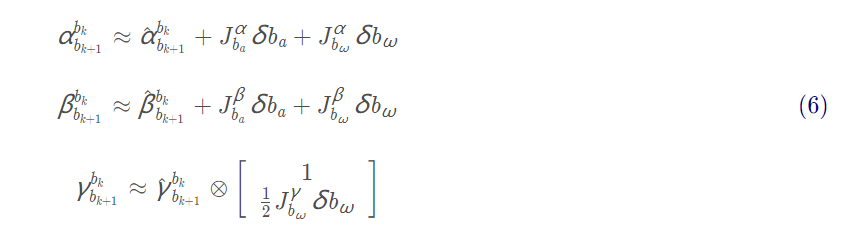
预积分误差

在上面的推导中引入误差的不仅仅是将变换的Bias视为不变，还存在加速度计和陀螺仪的噪声，同时位置、速度和角度之间的误差也会相互影响，并且误差是随时间一直累计的，因此，我们直接给出误差的状态方程，也就是误差变化的情况，通过误差的变化以及上一时刻累计的误差我们就可以求得下一时刻的误差：（这里误差的传递由两部分组成：当前时刻的误差传递给下一时刻+当前时刻测量噪声传给下一个时刻）

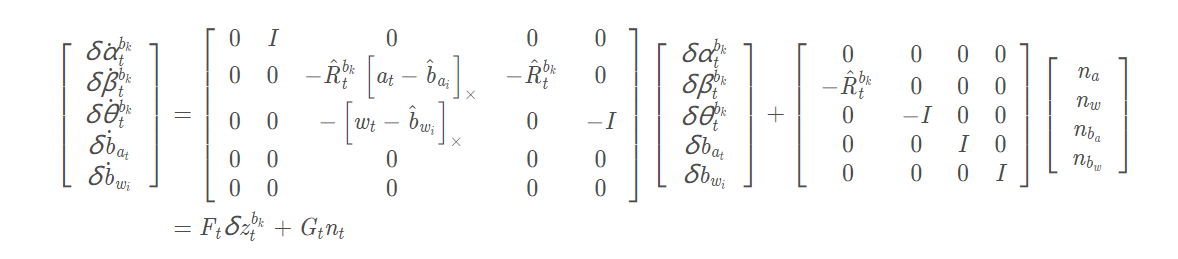
那么根据导数的定义有上一时刻推导下一时刻的误差如下：

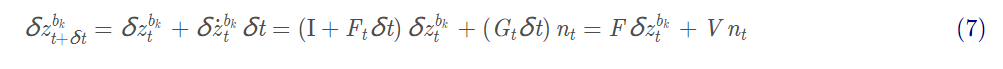
类比EKF的运动转移方程（其实也是把一个原本非线性的方程线性化），我们类似给出误差的协方差变化：

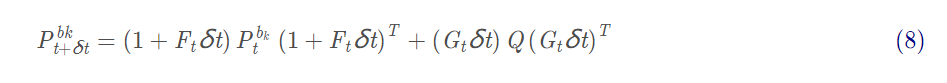
F为Xk对Xk-1的雅可比矩阵
G为Xk对Uk-1（输入量）的雅可比矩阵

因为上面的方程是线性方程，那么我们的状态转移方程关于δ的雅克比矩阵也可以递推出来：

上面的公式都是在连续时间推导的（t嘛）所以我们下面对应进行离散化一下：
(7)式离散形式为：

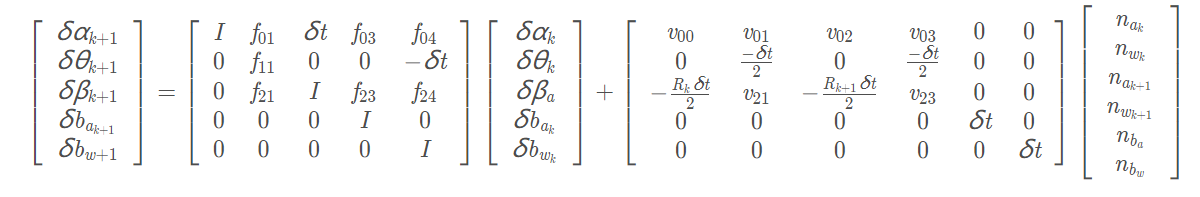
其中

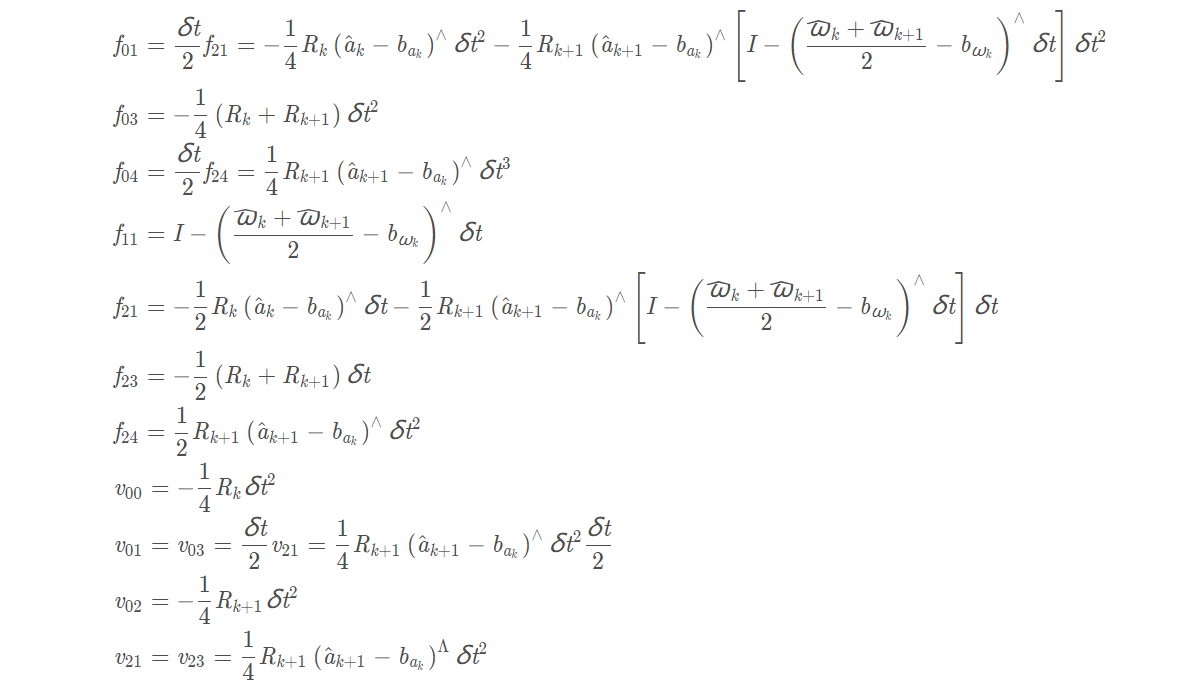
这里最后计算出来的协方差矩阵其实是观测值对应的权值（因为有很多观测值）。

最后

以上就是苹果彩虹为你收集整理的淦VINS-MONO源码 02--VIO中的预积分推导VIO中的预积分推导的全部内容，希望文章能够帮你解决淦VINS-MONO源码 02--VIO中的预积分推导VIO中的预积分推导所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。