概述
1.激光雷达（激光测距雷达）
1.1 传感器介绍
基于三角测距原理的传感器
主要简单介绍三角测距原理。
原理如下图，A是接收器镜头，B是激光发射器；L,α,β均是已知量。
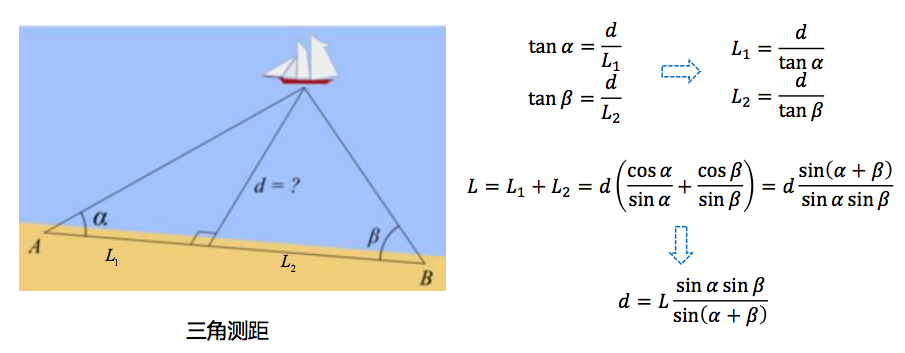
基于TOF测距原理的传感器
主要简单介绍TOF测距原理。
TOF是飞行时间(Time of Flight)的简写。
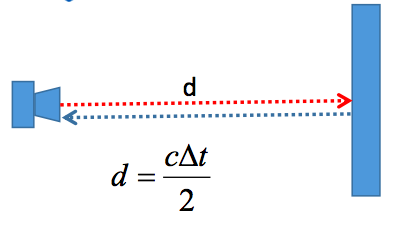
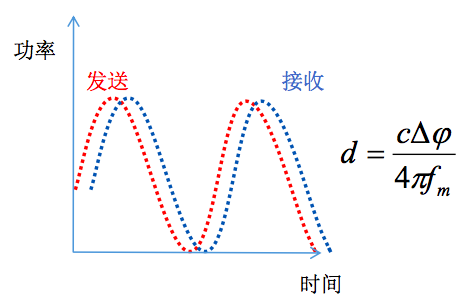
波形相位差测距原理，精度较TOF高
传感器比较
| 优点 | 不足 | 适用场景 | |
|---|---|---|---|
| 三角测距特点 | 中近距离精度较高；价格便宜 | 远距离精度较差；易受干扰 | 一般在室内使用（如扫地机器人） |
| TOF特点 | 测距范围广；测距精度高；抗干扰能力强 | 价格昂贵 | 室内室外皆可 |
1.2 数学模型介绍
1.2.1 波束模型
介绍
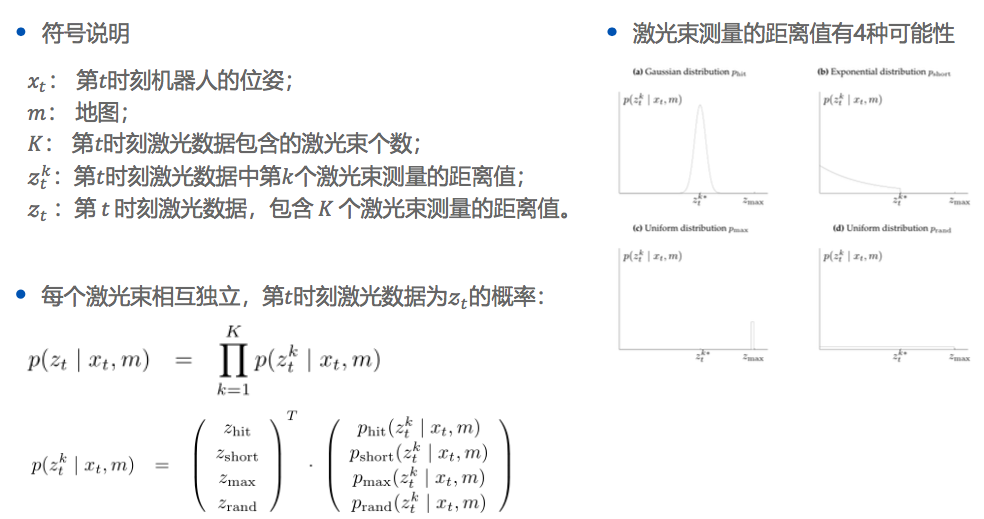
缺点
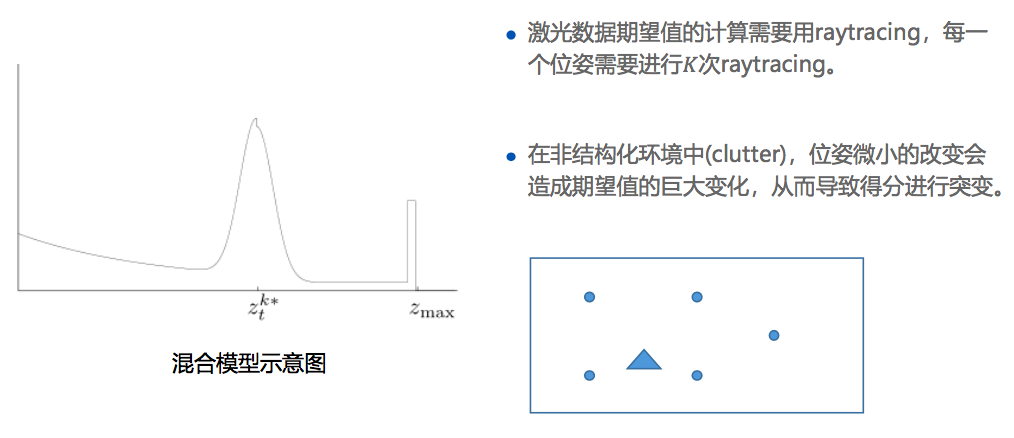
1.2.2 似然域模型
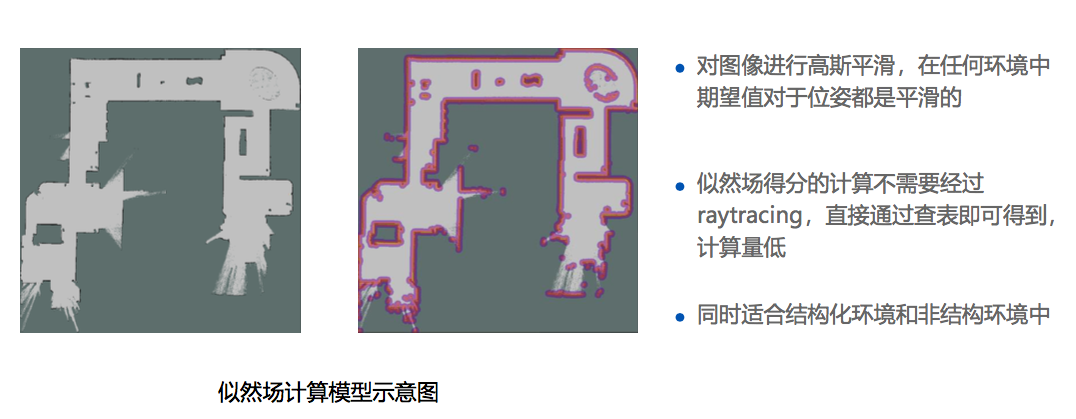
2.运动畸变
2.1 原因
运动畸变产生的原因
- 激光点数据不是瞬时获得
- 激光测量时伴随着机器人的运动
- 激光帧率较低时，机器人的运动不能忽略
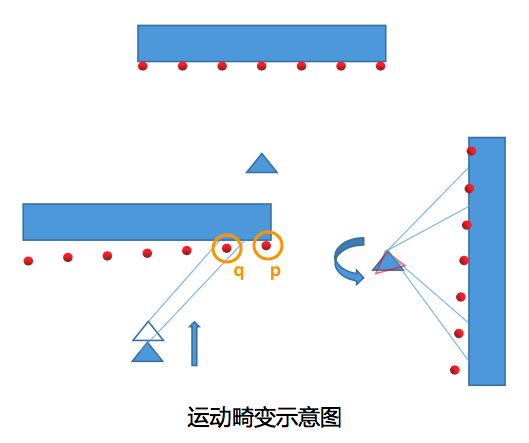
2.2 去除
2.2.1 纯估计方法
ICP方法
求解两个点云集合转换关系的最通用的方法。
数学描述
给定两个点云集合X , P
求解旋转矩阵R 和平移向量t ，使得下式最小
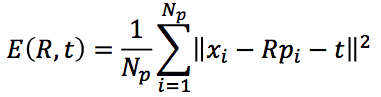
求解方法
已知对应点
1、求点云集合X , P X,PX,P的几何中心u x , u p
2、点云集合X , P 中的点去中心化
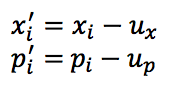
3、SVD分解
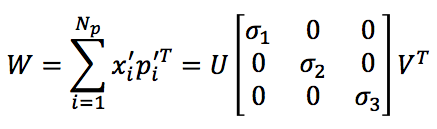
4、ICP的解
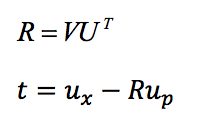
未知对应点（大多数情况）
实际中，一般是不知道对应点匹配的，不能一步到位计算出R 和t，因此需要迭代计算，用到期望最大化(Expectation Maximization,EM)的思想。
流程
- 寻找对应点（找最近的点）
- 根据对应点，计算R 和t
- 对点云进行转换，计算误差
- 不断迭代，直至误差小于某一个值
VICP方法
ICP方法没有考虑激光的运动畸变以及出现错误的激光数据。
VICP方法
- ICP方法的变种
- 考虑了机器人的运动
- 匀速运动
- 进行匹配的同时估计机器人的速度
描述
流程
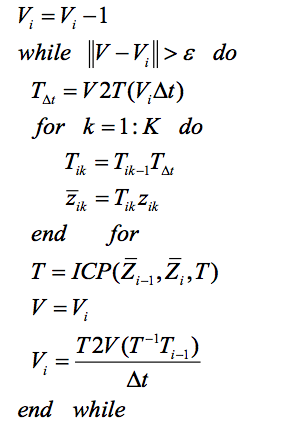
效果
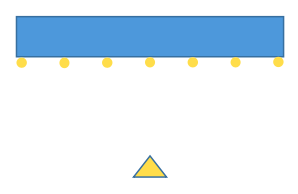
2.2.2 里程计辅助方法（本次重点）
VICP方法缺点
- 低帧率激光(5HZ)，匀速运动假设不成立
- 数据预处理和状态估计过程耦合
解决方法
- 尽可能准确地反映运动情况
- 实现预处理和状态估计的解耦
引出传感器辅助方法(里程计/IMU)
- 极高的位姿更新频率(200HZ)，可以比较准确地反应运动情况
- 较高精度的局部位姿估计
- 跟状态估计完全解耦
对比
IMU与轮式里程计对比
| IMU× | 轮式里程计√ |
|---|---|
| 直接测量角速度和线加速度 | 直接测量机器人的位移和角度 |
| 具有较高的角速度测量精度 | 具有较高的局部角度测量精度 |
| 测量频率极高(1kHz~8kHz) | 具有较高的局部位置测量精度 |
| 线加速度精度太差，二次积分在局部的精度依然很差× | 更新速度较高(100Hz~200Hz)√ |
在单片机和处理器上处理对比
| 单片机× | 处理器√ |
|---|---|
| 用单片机读取激光雷达数据，每次读取激光点数据时都可以获取当时机器人的位姿，根据机器人位姿消除运动畸变。得到一帧完整的数据后，上传至处理器 | 用CPU读取激光雷达数据，同时单片机上传里程计积分数据，两者进行时间同步。 在CPU上统一进行运动畸变去除 |
| 在单片机层消除运动畸变 | 体系清晰，不会产生延时 |
| 无需考虑时间同步的问题 | 需要进行时间同步 |
| 需要对数据进行压缩，否则会产生较大延时× | 需要进行位姿插值√ |
目的
通过已知量求未知量。
已知量
- 当前帧激光起始时间结束时间：t s , t e
- 两个激光束之间的时间间隔：Δ t
且满足以下条件
- 里程计数据按照时间顺序存储在一个队列中
FIFO，队首数据时间最早，队尾数据时间最晚。 - 最早的里程计数据的时间戳<t s
- 最晚的里程计数据的时间戳>t e
未知量（求解目标）
- 当前帧激光数据中每一个激光点对应的机器人位姿：p t s , p t s + Δ t , . . . , p t e
接下来
- 根据求解的位姿把所有激光点转换到同一坐标系下
- 重新封装成一帧激光数据，发布出去
过程
求解t s , t e t_s,t_ets,te时刻的位姿p s , p e
利用p l , p k 可以线性插值得到一条直线L 1 ，而l < s < k ，可得出p s p_sps，p e 求解过程类似。
二次插值
使用线性插值得到机器人在t s , t e ,te中间时刻t m 的位姿p m
假设在一帧激光数据之间，认为机器人做匀加速运动，因此机器人的位姿是关于时间t tt的二次函数。
已知p s , p m , p e ，二次插值近似该二次函数得到二次曲线L 2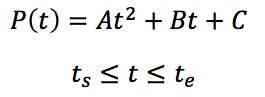 
二次曲线L 2 如下图
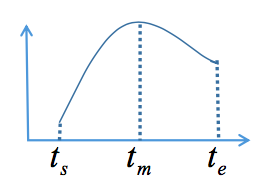
二次曲线的近似
目标
使用分段线性函数对二次曲线L 2进行近似
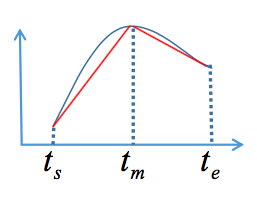
⚠️分段数大于3时，近似误差可以忽略不计，例如
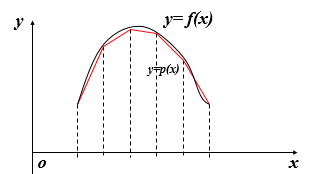
激光点坐标转换及激光数据发布
2.2.3 融合方法
将纯估计方法与里程计辅助方法结合，过程如下
- 用里程计辅助方法进行矫正，去除绝大部分的运动畸变
- 认为里程计存在误差，但是误差值是线性分布的
- 用ICP的方法进行匹配，匹配的结果作为正确值，得到里程计的误差值
- 把误差值均摊到每一个点上，重新进行激光点位置修正
- 再一次进行ICP迭代，直到收敛为止
⚠️位置误差的线性假设比位置线性假设更合理
3.附录
线性插值
几何意义
用过两插值节点的直线近似原函数。
如图，利用过点(x 0 , y 0 )和(x 1 , y 1 )的直线L ( x ) 来近似原函数f ( x ) 。
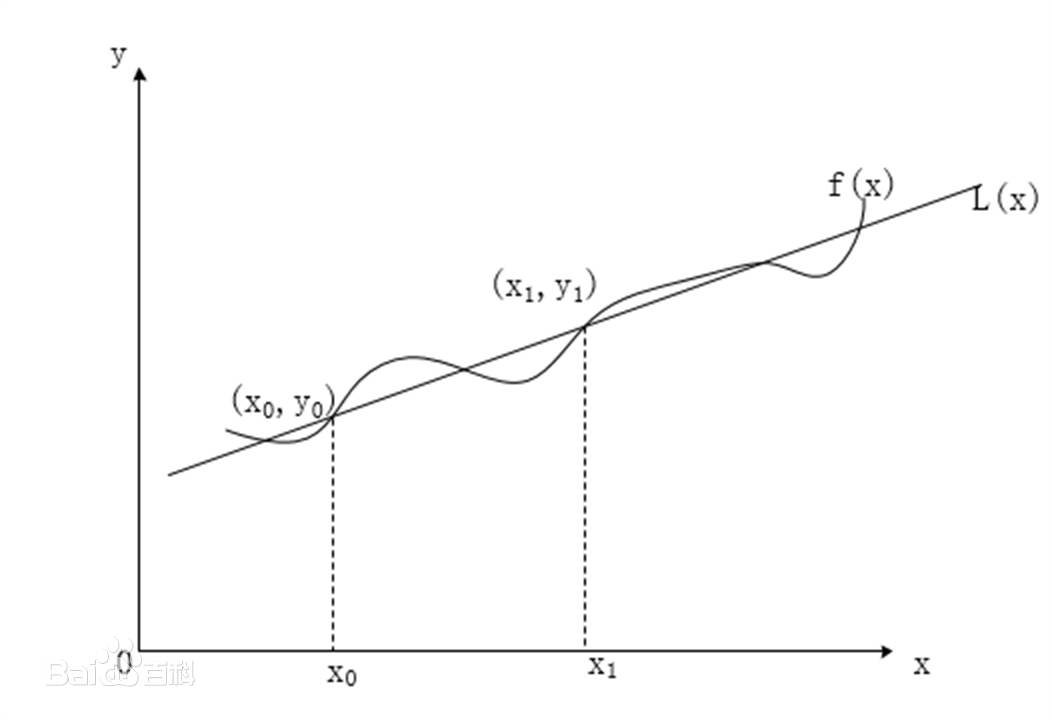
过程
线性插值百度百科
二次插值（抛物线法）
几何意义
过程
抛物线法百度百科
最后
以上就是炙热可乐为你收集整理的激光雷达运动畸变去除1.激光雷达（激光测距雷达）2.运动畸变3.附录的全部内容，希望文章能够帮你解决激光雷达运动畸变去除1.激光雷达（激光测距雷达）2.运动畸变3.附录所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复