基本概念

字母表 (Alphabet)

字母表∑是一个有穷符号集合
#符号：字母、数字、标点符号、…
#例：

• 二进制字母表：{ 0,1 }
• ASCII字符集
• Unicode字符集

字母表上的运算

字母表∑1和∑2的乘积( product)

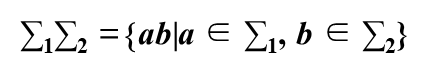
例： {0, 1} {a, b} ={0a, 0b, 1a, 1b}

字母表∑的n次幂( power)

#字母表的n次幂：长度为n的符号串构成的集合

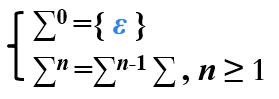
例： {0, 1}³ ={0, 1} {0, 1} {0, 1}
={000, 001, 010, 011, 100, 101, 110, 111}

字母表∑的正闭包( positive closure)

#字母表的正闭包：长度正数的符号串构成的集合

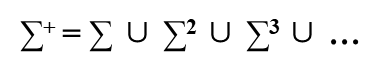
例：{a, b, c, d }⁺ = {a, b, c, d,
aa, ab, ac, ad, ba, bb, bc, bd, …,
aaa, aab, aac, aad, aba, abb, abc, …}

字母表∑的克林闭包(Kleene closure)

#字母表的克林闭包：任意符号串（长度可以为零）构成的集合

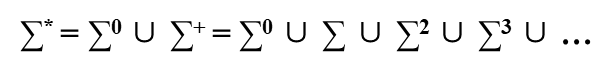
例：{a, b, c, d }* = {ε, a, b, c, d,
aa, ab, ac, ad, ba, bb, bc, bd, …,
aaa, aab, aac, aad, aba, abb, abc, …}

串(String)

设∑是一个字母表，∀x∈∑*，x称为是∑上的一个串
串是字母表中符号的一个有穷序列
串s的长度，通常记作|s|，是指s中符号的个数
例: |aab|=3
空串是长度为0的串，用 ε（epsilon）表示
|ε|= 0

串上的运算

连接

如果 x和y是串，那么x和y的连接(concatenation)
是把y附加到x后面而形成的串，记作xy
例如，如果 x=dog且 y=house，那么xy=doghouse

空串是连接运算的单位元( identity)，即，对于任何串s都有，εs = sε = s
设x,y,z是三个字符串，如果 x=yz，则称y是x的前缀，z是x的后缀
如：x=yz=doghouse，y=dog是x的前缀，z=house是x的后缀

幂

串s的幂运算:将n个s连接起来

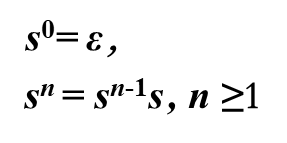
s1 = s0 s = εs = s，s2 = ss，s3 = sss，…
例：如果 s =ba，那么s¹= ba，s²=baba，s³=bababa，…

文法的定义

我们先看

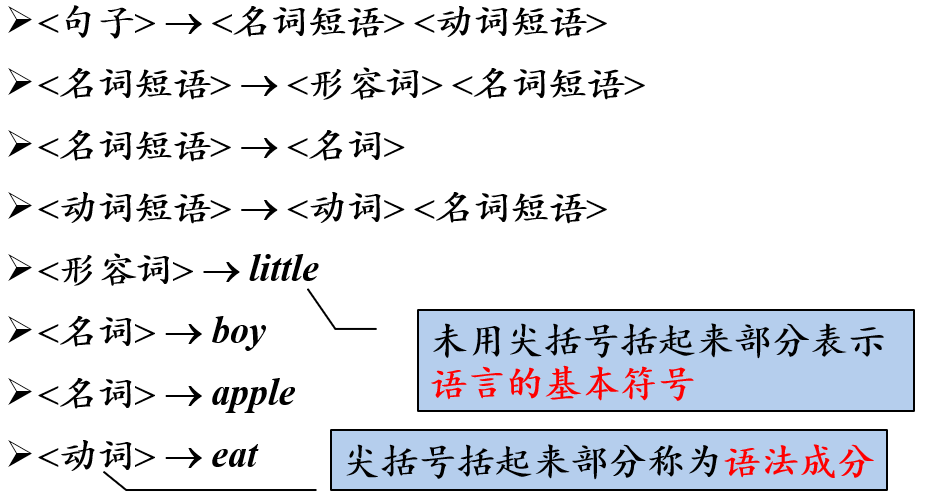
自然语言的句子的构成规则

然后尝试

形式化定义文法

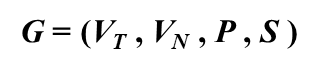
V_T ：终结符集合

终结符（terminal symbol）是文法所定义的语言的基本符号，有时也称为token
例: V_T = { apple, boy, eat, little }

V_N：非终结符集合

非终结符(nonterminal) 是用来表示语法成分的符号，有时也称为“ 语法变量”
例: V_N = { <句子>, <名词短语>, <动词短语>, <名词>, … }

P ：产生式集合

产生式( production)**描述了将终结符和非终结符组合成串**的方法

＃＃ 产生式的一般形式：
α→β
读作：α定义为β
α∈(V_T∪V_N)⁺，且α中至少包含VN中的一个元素：称为产生式的头(head)或左部(left side)
β∈(V_T∪V_N)* ：称为产生式的体(body)或右部(right side)

S ：开始符号

S∈V_N 开始符号(start symbol)表示的是该文法中最大的语法成分
例：S = <句子>

一个完整的文法

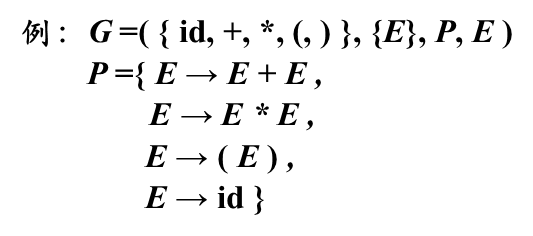
约定：
不引起歧义的前提下，可以只写产生式
即：

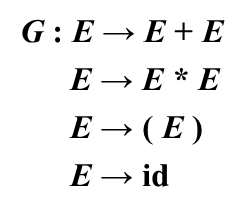
符号约定

1.一般的终结符有：
(1) 字母表中排在前面的小写字母，如 a、b、c
(2) 运算符，如 +、*等
(3) 标点符号，如括号、逗号等
(4) 数字0、1、. . . 、9
(5) 粗体字符串，如id、if等
2.一般的非终结符有：
(1) 字母表中排在前面的大写字母，如A、B、 C
(2) 字母S。通常表示开始符号
(3) 小写、斜体的名字，如 expr、stmt等
(4) 代表程序构造的大写字母。如E(表达式)、T(项)和F(因子)
3.字母表中排在后面的大写字母（如X、Y、Z）表示文法符号（即终结符或非终结符）
4.字母表中排在后面的小写字母（主要是u、v、. . . 、z） 表示终结符号串（包括空串）
5.小写希腊字母，如α、β、γ，表示文法符号串（包括空串）
6.除非特别说明，第一个产生式的左部就是开始符号

语言的定义

首先明确

推导 (Derivations)和归约(Reductions)

几点说明：

推导与是归约在语言上的不同角度：

句型和句子

句型

句子

语言上的运算

例：令L={A，B，…，Z，a，b，…，z}，D={0，1，…，9}。则L(L∪D)*表示的语言是标识符

Chomsky 文法的分类

• 0型文法 (Type-0 Grammar)
• 1型文法 (Type-1 Grammar)
• 2型文法 (Type-2 Grammar)
• 3型文法 (Type-3 Grammar)

各方法关系

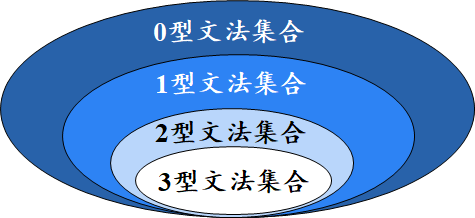
0型文法 (Type-0 Grammar)

又名无限制文法(Unrestricted Grammar) /短语结构文法 (Phrase Structure Grammar, PSG )
顾名思义，几乎没有什么限制。
要说有限制，下面这个算一个吧
∀α → β∈P， α中至少包含1个非终结符

0型语言：由0型文法G生成的语言L(G )

1型文法 (Type-1 Grammar)

又名上下文有关文法(Context-Sensitive Grammar , CSG )
∀α → β∈P，｜α｜≤｜β｜  //产生式头的长度小于体即CSG中不包含ε-产生式
产生式的一般形式： α₁Aα₂ → α₁βα₂ ( β≠ε )

上下文有关语言（1型语言）：由上下文有关文法 (1型文法) G生成的语言L(G )

2型文法 (Type-2 Grammar)

又名上下文无关文法 (Context-Free Grammar, CFG )
∀α → β∈P，α ∈ V_N   //  V_N表非终结符集合
产生式的一般形式：A→β
例：

S → L | LT
T → L | D | TL | TD 
L → a | b | c | d |…| z
D → 0 | 1 | 2 | 3 |…| 9

上下文无关语言（2型语言）：由上下文无关文法 (2型文法) G生成的语言L(G )

3型文法 (Type-3 Grammar)

又名正则文法 (Regular Grammar, RG )
分为

• 右线性(Right Linear)文法： A→wB 或 A→w
• 左线性(Left Linear) 文法： A→Bw 或 A→w

左线性文法和右线性文法都称为正则文法

例（右线性文法）
① S → a | b | c | d 
② S → aT | bT | cT | dT 
③ T → a | b | c | d | 0 | 1 | 2 | 3 | 4 | 5
④ T → aT | bT | cT | dT | 0T | 1T | 2T | 3T | 4T | 5T   //标识符文法
与下面此方法相当
文法G（ 上下文无关文法）
① S → L | LT
② T → L | D | TL | TD 
③ L → a | b | c | d
④ D → 0 | 1 | 2 | 3 | 4 | 5

正则语言（3型语言）：由正则文法 (3型文法) G生成的语言L(G )
//正则文法能描述程序设计语言的多数单词

小总结：

• 0型文法：α中至少包含1个非终结符
• 1型文法（CSG） ：｜α｜≤｜β｜
• 2型文法（CFG） ：α ∈ V_N
• 3型文法（RG）：A→wB 或 A→w (A→Bw 或A→w)

CFG的分析树

分析树由啥子组成

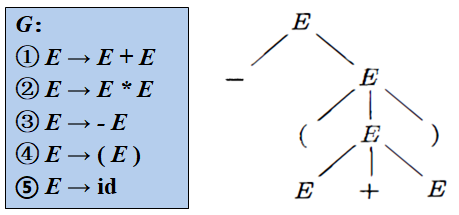
根节点的标号为文法开始符号
内部结点表示对一个产生式A→β的应用，   //用人话来说大概就是E → - E 表示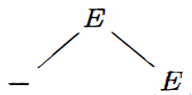

• 该结点的标号是此产生式左部A 。                   ↑
• 该结点的子结点的标号从左到右构成了产生式的右部β。 //这两句说的就上面那句话

叶结点的标号既可以是非终结符，也可以是终结符。//重要的废话，划重点
从左到右排列叶节点得到的符号串称为是这棵树的产出( yield )或边缘(f rontier)  //如下图

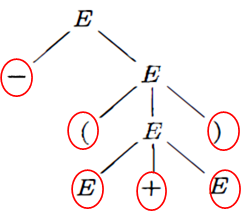
分析树是推导的图形化表示

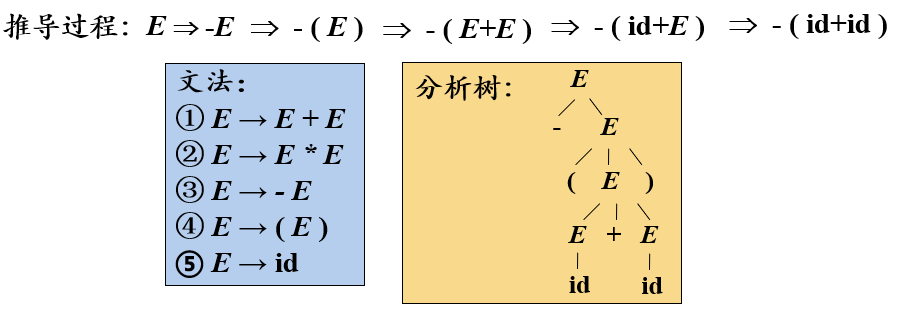
(句型的）短语

给定一个句型，其分析树中的每一棵子树的边缘称为该句型的一个短语(phrase)
//用下图说明就是
//第三行的E 以它为根结点的树的所有边缘（叶结点）构成了一个短语即E+E
如果子树只有父子两代结点，那么这棵子树的边缘称为该句型的一个直接短语（immediate phrase)
//就像第三行那个E一样。其它的高度都在2以上。

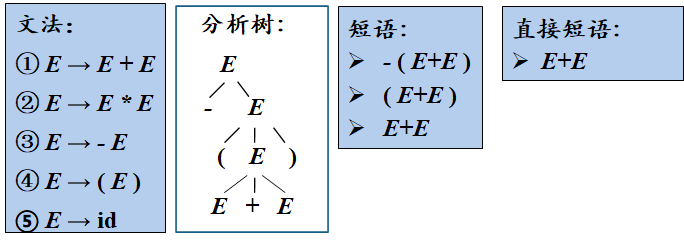
直接短语一定是某产生式的右部 //你想想他就是一个结点分岔了一次，也就是说只推导了一次，可不就直接只是文法中的某一个产生式。那那个子结点可不就是那个产生式的右部吗？
但产生式的右部不一定是给定句型的直接短语   //废话

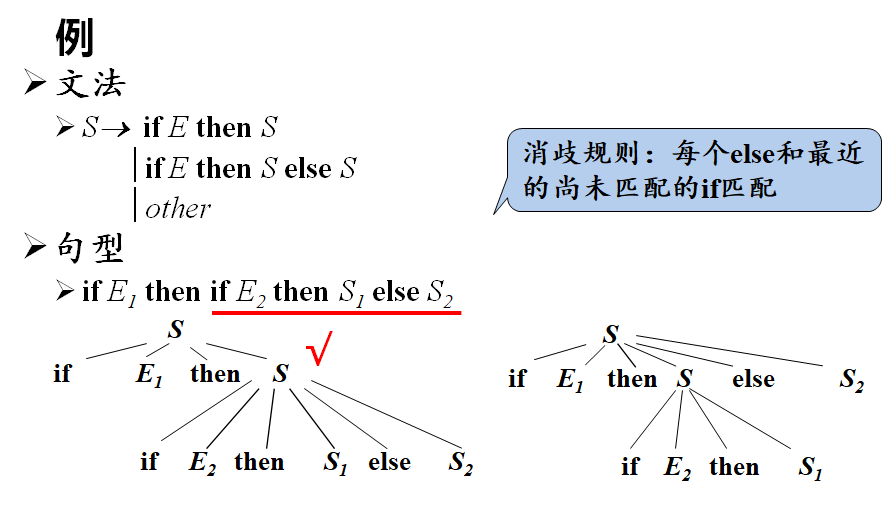
二义性文法 (Ambiguous Grammar)

如果一个文法可以为某个句子生成多棵分析树，则称这个文法是二义性的

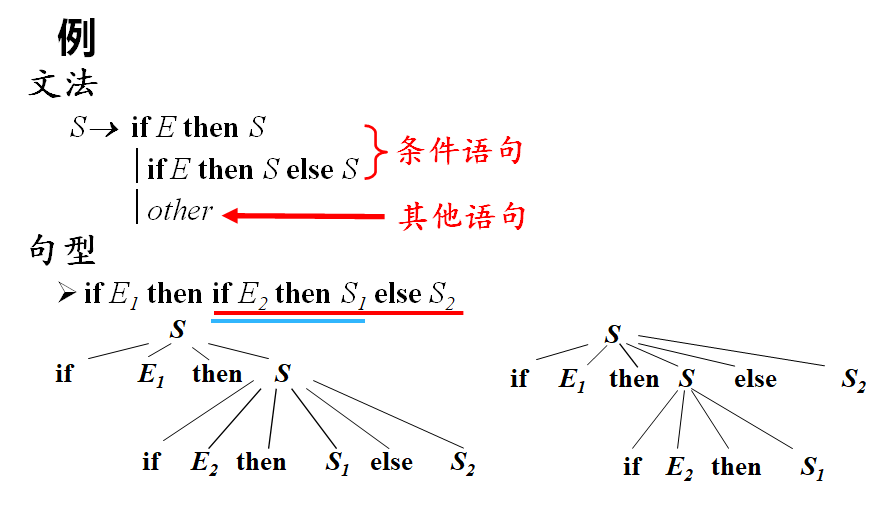
加入一个对应的消歧规则就可以避免二义性

怎么判定一个文法是否有二义性呢

对于任意一个上下文无关文法，不存在一个算法，判定它是无二义性的；//想屁吃
但能给出一组充分条件，满足这组充分条件的文法是无二义性的

• 满足，肯定无二义性
• 不满足，也未必就是有二义性的

内容参考哈工大编译原理陈鄞老师mooc

最后

以上就是纯情乌龟为你收集整理的编译原理笔记2 程序设计及其方法 龙书基本概念文法的定义语言的定义Chomsky 文法的分类CFG的分析树的全部内容，希望文章能够帮你解决编译原理笔记2 程序设计及其方法 龙书基本概念文法的定义语言的定义Chomsky 文法的分类CFG的分析树所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。