易错易忘收集（基于CS231n课程学习）

 axis=0为列方向

 axis=1为行方向

在axis方向上求。。。

verbose=True才打印

各种相乘：https://blog.csdn.net/zenghaitao0128/article/details/78715140

np.max：(a, axis=None, out=None, keepdims=False)求序列的最值,最少接收一个参数,axis：默认为列向（也即 axis=0），axis = 1 时为行方向的最值；

np.maximum：(X, Y, out=None),X 与 Y 逐位比较取其大者；最少接收两个参数

numpy.where(condition[, x, y])。一般使用时，返回的时tuple

numpy.sum 参数keepdims用于保证二维一致性

np.linalg.norm(）各种距离

np.bincount(np.array([0, 1, 1, 3, 2, 1, 7]))array([1, 3, 1, 1, 0, 0, 0, 1], dtype=int32) # 分别统计0-7分别出现的次数

X_train_folds = np.array_split(X_train, num_folds)

np.array_split()&np.split():https://blog.csdn.net/m0_37393514/article/details/79537639

np.vstack与np.hstack

plt.scatter([k]*len(accuracies),accuracies)，其中[k]重复len(accuracies)次

np.random.choice(num_training, num_dev,replace=False)

random.randrange(6)  含义为0-5随机选

enumerate() 

遍历dict：for k, v in list(data.items()):

np.prod(）所有元素乘积，同时可以设置axis计算某方向上的乘积

np.linspace(-0.1, 0.5,5)  5代表有5个，且结果包含左右边界。结果为array([-0.1 , 0.05, 0.2 , 0.35, 0.5 ])

np.all()  判断所有的元素是否全为true

np.tolist() 与np.array()是互操作

np.array(A),对A进行的复制操作，np.asarray()没有复制操作。

不能是tuple

np.random.randn(10, 10)  

必须是tuple

np.zeros((2,3))【为shape】

可以是tuple，也可以不是

np.reshape()

相当于瓦解tuple

1、range多用作循环，range（0,10）返回一个range对象，如想返回一个list，前面加上list转换；

2、arange是numpy模块中的函数，使用前需要先导入此模块，arange(3):返回array类型对象。

【注：range()中的步长不能为小数，但是np.arange()中的步长可以为小数】

3、xrange()也是用作循环，只是xrang(0,10)不返回list，返回xrange对象。每次调用返回其中的一个值。 但是好像xrange现在不能使用了。

返回很大的数的时候或者频繁的需要break时候，xrange性能更好。

np.random.randint(C,size=(N,))

scores[np.arange(num_train), y] ，np.arange(num_train)与y均是数组，则选择出scores的第i行第j列的元素（i，j分别为两数组里面的元素）

/代表浮点数相除，//代表整数相除。

为dict设置默认值：

if configis None: config = {}

config.setdefault('learning_rate',1e-2)

[0.5] *3代表[0.5,0.5,0.5]，其中[0.5]为一个列表而不是np.array,否则结果应该为[1.5]

lambda函数

f =lambda w: svm_loss_naive(w, X_dev, y_dev,1e2)[0]

a=np.array([[1,2],[3,4]])

a[0]为 array([1, 2])【第0行】，其实联想一下Java的数组就明白了。

方法1.用List的成员函数sort进行排序，在本地进行排序，不返回副本

方法2.用built-in函数sorted进行排序（从2.4开始），返回副本，原始输入不变

svm中展示权重图片

w=best_svm.W[:-1,:]

w=w.reshape((32,32,3,10))

w_min,w_max=np.min(w),np.max(w)

classes = ['plane','car','bird','cat','deer','dog','frog','horse','ship','truck']

for i in range(10):

    plt.subplot(2,5,i+1)

    wimg=255.0*(w[:,:,:,i].squeeze()-w_min)/(w_max - w_min)

    plt.imshow(wimg.astype('uint8'))

    plt.axis('off')

    plt.title(classes[i])

plt.imshow(visualize_grid(W1,padding=3).asty('uint8'))

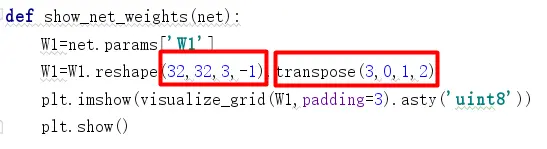
上图中，好像首先计算-1为50，然后分别按照50,3,32,32的顺序进行reshape

astype('uint8')的结果

dW = np.zeros_like(W)

np.zeros((3,2)),里面的（）不能去掉

replace = True 在一次抽取中，抽取的样本可重复出现。 

即：np.random.choice(6, 2, replace=True) 

可得，array( [4, 4] ) 

replace = False 再一次抽取中，抽样的样本不可重复出现。 

即：np.random.choice(6, 2, replace=True) 

a.reshape(N,1):返回一个N*1维的ndarray，并不会改变a的大小。

.resize(shape) ： 与.reshape()功能一致，但修改原数组

exp_sum = np.sum(A,axis=1).reshape(N,1)

A是一个矩阵，则np.sum(A,axis=1)的结果为一个数组（一行，此处仍然想想数组即可理解），但是我需要列向量，此时就需要reshape（N,1）^_^

flags=['multi_index']表示对a进行多重索引。op_flags=['readwrite']表示不仅可以对a进行read（读取），还可以write（写入），

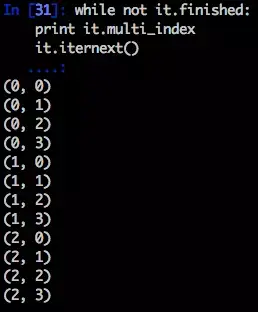
it = np.nditer(x,flags=['multi_index'],op_flags=['readwrite'])

while not it.finished:

       ix = it.multi_index

        it.iternext()

则每个ix是一个tuple ()，如下图：

在验证net梯度的正确性时，eval_numerical_gradient对net.params[param_name]进行修改时，是直接在net上的修改，所以lambda的参数没有意义，写任何字母均可。

for param_namein grads:

    f =lambda WWWW: net.loss(X, y,reg=0.1)[0]

    param_grad_num = eval_numerical_gradient(f, net.params[param_name],verbose=False)

im.ndim：输出维度

np.dot(rgb[...,:3], [0.299,0.587,0.144]) 将rgb转化为灰度图像，但是并不理解rgb[...,:3]的意思。

print

(1). %字符：标记转换说明符的开始

(2). 转换标志：-表示左对齐；+表示在转换值之前要加上正负号；“”（空白字符）表示正数之前保留空格；0表示转换值若位数不够则用0填充

(3). 最小字段宽度：转换后的字符串至少应该具有该值指定的宽度。如果是*，则宽度会从值元组中读出。

(4). 点(.)后跟精度值：如果转换的是实数，精度值就表示出现在小数点后的位数。如果转换的是字符串，那么该数字就表示最大字段宽度。如果是*，那么精度将从元组中读出

(5).字符串格式化转换类型

转换类型          含义

d,i                 带符号的十进制整数

o                   不带符号的八进制

u                   不带符号的十进制

x                    不带符号的十六进制（小写）

X                   不带符号的十六进制（大写）

e                   科学计数法表示的浮点数（小写）

E                   科学计数法表示的浮点数（大写）

f,F                 十进制浮点数

g                   如果指数大于-4或者小于精度值则和e相同，其他情况和f相同

G                  如果指数大于-4或者小于精度值则和E相同，其他情况和F相同

C                  单字符（接受整数或者单字符字符串）

r                    字符串（使用repr转换任意python对象)

s                   字符串（使用str转换任意python对象）

>>> pi =3.141592653  

>>>print('%10.3f' % pi)#字段宽10，精度3  

3.142  

>>>print("pi = %.*f" % (3,pi))#用*从后面的元组中读取字段宽度或精度  

pi =3.142  

>>>print('%010.3f' % pi)#用0填充空白  

000003.142  

>>>print('%-10.3f' % pi)#左对齐  

3.142       

>>>print('%+f' % pi)#显示正负号  

+3.141593  

最后

以上就是外向日记本为你收集整理的易错易忘收集（基于CS231n课程学习）的全部内容，希望文章能够帮你解决易错易忘收集（基于CS231n课程学习）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。