cs231n assignment1 KNN

需注意的几点：

• 在无循环计算时：

令测试集为P(m×d)，训练集为C(n×d)，m为测试数据数据量，n为训练数据数据量，d是维度。

实际上最后距离公式变为如下形式

这里实现的依然是广播，所以只要P的形状为 m×1，C的形状为 1×n即可

• 三种循环方式体现的是运算速度的不同，结果是一致的
• k = 1时，training data自身的匹自身为100%

直接执行的代码（注释掉测试部分）

KNN中，训练即存储

import pickle
import os
import numpy as np
import matplotlib.pyplot as plt
from cs231n.data_utils import load_CIFAR10
from cs231n.classifiers import KNearestNeighbor

# This is a bit of magic to make matplotlib figures appear inline in the notebook
# rather than in a new window.
plt.rcParams['figure.figsize'] = (10.0, 8.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

# Some more magic so that the notebook will reload external python modules;
# see http://stackoverflow.com/questions/1907993/autoreload-of-modules-in-ipython


# Load the raw CIFAR-10 data.
cifar10_dir = 'F:pycharmFileKNNcifar-10-batches-py'
X_train, y_train, X_test, y_test = load_CIFAR10(cifar10_dir)

# As a sanity check, we print out the size of the training and test data.
# print('Training data shape: ', X_train.shape)
# print('Training labels shape: ', y_train.shape)
# print('Test data shape: ', X_test.shape)
# print('Test labels shape: ', y_test.shape)

# Visualize some examples from the dataset.
# We show a few examples of training images from each class.
# classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
# num_classes = len(classes)
# samples_per_class = 7
# for y, cls in enumerate(classes):
#     idxs = np.flatnonzero(y_train == y)                                     # 返回非零元素
#     idxs = np.random.choice(idxs, samples_per_class, replace=False)         # 随机不放回地抽出7个
#     for i, idx in enumerate(idxs):
#         plt_idx = i * num_classes + y + 1
#         plt.subplot(samples_per_class, num_classes, plt_idx)
#         plt.imshow(X_train[idx].astype('uint8'))
#         plt.axis('off')
#         if i == 0:
#             plt.title(cls)
# # 查看样本
# plt.show()

# 取出子集， 用于train和test
# Subsample the data for more efficient code execution in this exercise
num_training = 5000
mask = range(num_training)
X_train = X_train[mask]
y_train = y_train[mask]

num_test = 500
mask = range(num_test)
X_test = X_test[mask]
y_test = y_test[mask]


# 将图像转置成二维
X_train = np.reshape(X_train, (X_train.shape[0], -1))
X_test = np.reshape(X_test, (X_test.shape[0], -1))
# print(X_train.shape, X_test.shape)

# KNN只将数据进行简单的存储
classifier = KNearestNeighbor()
#classifier.train(X_train, y_train)

# L2实现
#dists = classifier.compute_distances_two_loops(X_test)
# print(dists)

# print(dists.shape)
# 可视化training data和testing data的距离
# 深色表示距离小
# plt.imshow(dists, interpolation='none')
# plt.show()

# 开始test
# y_test_pred = classifier.predict_labels(dists, k=5)

# 打印正确率
# num_correct = np.sum(y_test_pred == y_test)
# accuracy = float(num_correct) / num_test
# print('Got %d / %d correct ==> accuracy: %f' %(num_correct, num_test, accuracy))

# 一层循环
# dists_one = classifier.compute_distances_one_loop(X_test)
# difference = np.linalg.norm(dists - dists_one, ord='fro')
# print('Difference was: %f' % (difference, ))
# if difference < 0.001:
#   print('Good! The distance matrices are the same')
# else:
#   print('Uh-oh! The distance matrices are different')

# 无循环
# dists_two = classifier.compute_distances_no_loops(X_test)
#
# difference = np.linalg.norm(dists - dists_one, ord='fro')
# print('Difference was: %f' % (difference, ))
# if difference < 0.001:
#   print('Good! The distance matrices are the same')
# else:
#   print('Uh-oh! The distance matrices are different')


# Let's compare how fast the implementations are
# def time_function(f, *args):
#   """
#   Call a function f with args and return the time (in seconds) that it took to execute.
#   """
#   import time
#   tic = time.time()
#   f(*args)
#   toc = time.time()
#   return toc - tic

# two_loop_time = time_function(classifier.compute_distances_two_loops, X_test)
# print('Two loop version took %f seconds' % two_loop_time)
#
# one_loop_time = time_function(classifier.compute_distances_one_loop, X_test)
# print('One loop version took %f seconds' % one_loop_time)

# no_loop_time = time_function(classifier.compute_distances_no_loops, X_test)
# print('No loop version took %f seconds' % no_loop_time)

通过交叉验证找到最好的k

# 交叉验证
num_folds = 5
k_choices = [1, 3, 5, 8, 10, 12, 15, 20, 50, 100]

X_train_folds = []
y_train_folds = []

X_train_folds = np.array_split(X_train, num_folds, axis=0)
y_train_folds = np.array_split(y_train, num_folds, axis=0)


# A dictionary holding the accuracies for different values of k that we find
# when running cross-validation. After running cross-validation,
# k_to_accuracies[k] should be a list of length num_folds giving the different
# accuracy values that we found when using that value of k.
k_to_accuracies = {}

for k in k_choices:

    k_to_accuracies[k] = []
    for val_idx in range(num_folds):
        X_val = X_train_folds[val_idx]
        y_val = y_train_folds[val_idx]

        X_tra = X_train_folds[:val_idx] + X_train_folds[val_idx + 1:]
        X_tra = np.reshape(X_tra, (X_train.shape[0] - X_val.shape[0], -1))
        y_tra = y_train_folds[:val_idx] + y_train_folds[val_idx + 1:]
        y_tra = np.reshape(y_tra, (X_train.shape[0] - X_val.shape[0],))

        classifier.train(X_tra, y_tra)
        y_val_pre = classifier.predict(X_val, k, 0)

        right_arr = y_val_pre == y_val
        accuracy = float(np.sum(right_arr)) / y_val.shape[0]
        k_to_accuracies[k].append(accuracy)


# Print out the computed accuracies
for k in sorted(k_to_accuracies):
    for accuracy in k_to_accuracies[k]:
        print('k = %d, accuracy = %f' % (k, accuracy))

根据所得结果画出散点图，误差曲线 

# plot the raw observations
print(k_choices)
print(k_to_accuracies)
for k in k_choices:
  accuracies = k_to_accuracies[k]
  plt.scatter([k] * len(accuracies), accuracies)

# 画出散点图和误差曲线
accuracies_mean = np.array([np.mean(v) for k,v in sorted(k_to_accuracies.items())])
accuracies_std = np.array([np.std(v) for k,v in sorted(k_to_accuracies.items())])
plt.errorbar(k_choices, accuracies_mean, yerr=accuracies_std)
plt.title('Cross-validation on k')
plt.xlabel('k')
plt.ylabel('Cross-validation accuracy')
plt.show()

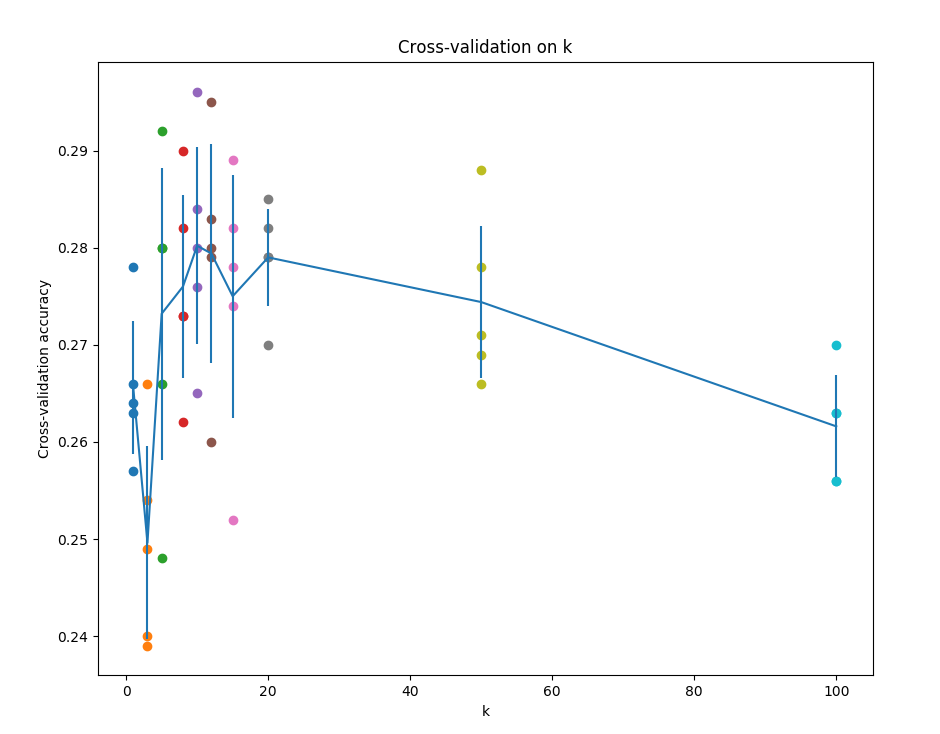
选择最好的k，此处当k=10时， 结果最好

best_k = 10

classifier = KNearestNeighbor()
classifier.train(X_train, y_train)
y_test_pred = classifier.predict(X_test, k=best_k)

# Compute and display the accuracy
num_correct = np.sum(y_test_pred == y_test)
accuracy = float(num_correct) / num_test
print('Got %d / %d correct => accuracy: %f' % (num_correct, num_test, accuracy))

修改原文件中的部分代码：

nearest_neighbor.py

import numpy as np

class KNearestNeighbor(object):
  """ a kNN classifier with L2 distance """

  def __init__(self):
    pass

  def train(self, X, y):
    """
    Train the classifier. For k-nearest neighbors this is just 
    memorizing the training data.

    Inputs:
    - X: A numpy array of shape (num_train, D) containing the training data
      consisting of num_train samples each of dimension D.
    - y: A numpy array of shape (N,) containing the training labels, where
         y[i] is the label for X[i].
    """
    self.X_train = X
    self.y_train = y
    
  def predict(self, X, k=1, num_loops=0):
    """
    Predict labels for test data using this classifier.

    Inputs:
    - X: A numpy array of shape (num_test, D) containing test data consisting
         of num_test samples each of dimension D.
    - k: The number of nearest neighbors that vote for the predicted labels.
    - num_loops: Determines which implementation to use to compute distances
      between training points and testing points.

    Returns:
    - y: A numpy array of shape (num_test,) containing predicted labels for the
      test data, where y[i] is the predicted label for the test point X[i].  
    """
    if num_loops == 0:
      dists = self.compute_distances_no_loops(X)
    elif num_loops == 1:
      dists = self.compute_distances_one_loop(X)
    elif num_loops == 2:
      dists = self.compute_distances_two_loops(X)
    else:
      raise ValueError('Invalid value %d for num_loops' % num_loops)

    return self.predict_labels(dists, k=k)

  def compute_distances_two_loops(self, X):
    """
    Compute the distance between each test point in X and each training point
    in self.X_train using a nested loop over both the training data and the 
    test data.

    Inputs:
    - X: A numpy array of shape (num_test, D) containing test data.

    Returns:
    - dists: A numpy array of shape (num_test, num_train) where dists[i, j]
      is the Euclidean distance between the ith test point and the jth training
      point.
    """
    num_test = X.shape[0]
    num_train = self.X_train.shape[0]
    dists = np.zeros((num_test, num_train))
    for i in range(num_test):
      for j in range(num_train):
        #####################################################################
        # TODO:                                                             #
        # Compute the l2 distance between the ith test point and the jth    #
        # training point, and store the result in dists[i, j]. You should   #
        # not use a loop over dimension.                                    #
        #####################################################################
        dists[i, j] = np.sqrt(np.sum(np.square(self.X_train[j] - X[i])))
        #####################################################################
        #                       END OF YOUR CODE                            #
        #####################################################################
    return dists

  def compute_distances_one_loop(self, X):
    """
    Compute the distance between each test point in X and each training point
    in self.X_train using a single loop over the test data.

    Input / Output: Same as compute_distances_two_loops
    """
    num_test = X.shape[0]
    num_train = self.X_train.shape[0]
    dists = np.zeros((num_test, num_train))
    for i in range(num_test):
      #######################################################################
      # TODO:                                                               #
      # Compute the l2 distance between the ith test point and all training #
      # points, and store the result in dists[i, :].                        #
      #######################################################################
      dists[i,:] = np.sqrt(np.sum(np.square(self.X_train - X[i,:]),axis=1))
      #######################################################################
      #                         END OF YOUR CODE                            #
      #######################################################################
    return dists

  def compute_distances_no_loops(self, X):
    """
    Compute the distance between each test point in X and each training point
    in self.X_train using no explicit loops.

    Input / Output: Same as compute_distances_two_loops
    """
    num_test = X.shape[0]
    num_train = self.X_train.shape[0]
    dists = np.zeros((num_test, num_train)) 
    #########################################################################
    # TODO:                                                                 #
    # Compute the l2 distance between all test points and all training      #
    # points without using any explicit loops, and store the result in      #
    # dists.                                                                #
    #                                                                       #
    # You should implement this function using only basic array operations; #
    # in particular you should not use functions from scipy.                #
    #                                                                       #
    # HINT: Try to formulate the l2 distance using matrix multiplication    #
    #       and two broadcast sums.                                         #
    #########################################################################
    dists = np.multiply(np.dot(X, self.X_train.T), -2)
    sq1 = np.sum(np.square(X), axis=1, keepdims=True)
    # keepdims = True, 使计算后依然为维度是测试样本数量的列向量、
    sq2 = np.sum(np.square(self.X_train),axis=1)
    dists = np.add(dists,sq1)
    dists = np.add(dists,sq2)
    dists = np.sqrt(dists)

    #########################################################################
    #                         END OF YOUR CODE                              #
    #########################################################################
    return dists

  def predict_labels(self, dists, k=1):
    """
    Given a matrix of distances between test points and training points,
    predict a label for each test point.

    Inputs:
    - dists: A numpy array of shape (num_test, num_train) where dists[i, j]
      gives the distance betwen the ith test point and the jth training point.

    Returns:
    - y: A numpy array of shape (num_test,) containing predicted labels for the
      test data, where y[i] is the predicted label for the test point X[i].  
    """
    num_test = dists.shape[0]
    y_pred = np.zeros(num_test)
    for i in range(num_test):
      # A list of length k storing the labels of the k nearest neighbors to
      # the ith test point.
      closest_y = self.y_train[np.argsort(dists[i])[:k]] #将矩阵按照axis排序，并返回排序后的下标
      y_pred[i] = np.argmax(np.bincount(closest_y))
      #########################################################################
      # TODO:                                                                 #
      # Use the distance matrix to find the k nearest neighbors of the ith    #
      # testing point, and use self.y_train to find the labels of these       #
      # neighbors. Store these labels in closest_y.                           #
      # Hint: Look up the function numpy.argsort.                             #
      #########################################################################
      pass
      #########################################################################
      # TODO:                                                                 #
      # Now that you have found the labels of the k nearest neighbors, you    #
      # need to find the most common label in the list closest_y of labels.   #
      # Store this label in y_pred[i]. Break ties by choosing the smaller     #
      # label.                                                                #
      #########################################################################
      pass
      #########################################################################
      #                           END OF YOUR CODE                            # 
      #########################################################################

    return y_pred

最终结果：

KNN在物体识别，数据量有限的情况下，比较弱

最后

以上就是怕黑猎豹为你收集整理的cs231n assignment1 KNN的全部内容，希望文章能够帮你解决cs231n assignment1 KNN所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。