对应HDU题目:点击打开链接
Picture
| Time Limit: 2000MS | Memory Limit: 32768KB | 64bit IO Format: %I64d & %I64u |
Description
A number of rectangular posters, photographs and other pictures of the same shape are pasted on a wall. Their sides are all vertical or horizontal. Each rectangle can be partially or totally covered by the others. The length of the boundary of the union of all rectangles is called the perimeter.
Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1.

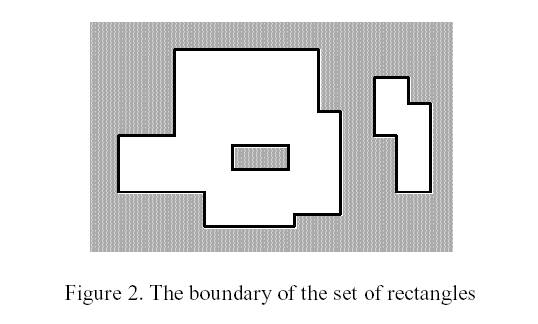
The corresponding boundary is the whole set of line segments drawn in Figure 2.
The vertices of all rectangles have integer coordinates.
Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1.

The corresponding boundary is the whole set of line segments drawn in Figure 2.

The vertices of all rectangles have integer coordinates.
Input
Your program is to read from standard input. The first line contains the number of rectangles pasted on the wall. In each of the subsequent lines, one can find the integer coordinates of the lower left vertex and the upper right vertex of each rectangle. The values of those coordinates are given as ordered pairs consisting of an x-coordinate followed by a y-coordinate.
0 <= number of rectangles < 5000
All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area.
Please process to the end of file.
0 <= number of rectangles < 5000
All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area.
Please process to the end of file.
Output
Your program is to write to standard output. The output must contain a single line with a non-negative integer which corresponds to the perimeter for the input rectangles.
Sample Input
7 -15 0 5 10 -5 8 20 25 15 -4 24 14 0 -6 16 4 2 15 10 22 30 10 36 20 34 0 40 16
Sample Output
228
Source
题意:矩阵周长并
思路:线段树扫描线,先从下往上扫,求出所有横边;再从左往右扫,求出所有竖边,最后相加。还有别的办法有空补上。。。
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<map>
#include<queue>
#include<stack>
#include<vector>
#include<algorithm>
#include<cstring>
#include<string>
#include<iostream>
const int MAXN=10000+10;
#define ms(x,y) memset(x,y,sizeof(x))
using namespace std;
int x[MAXN];
int y[MAXN];
int sum[MAXN<<2];
int cnt[MAXN<<2];
struct Line
{
int l,a,b;
int flag;
}line_y[MAXN],line_x[MAXN];
bool cmp(Line l1, Line l2)
{
return l1.l < l2.l;
}
void up(int rt, int left, int right, int *A)
{
if(cnt[rt]) sum[rt] = A[right+1] - A[left];
else if(left == right) sum[rt] = 0;
else sum[rt] = sum[rt<<1] + sum[rt<<1|1];
}
void update(int rt, int left, int right, int l, int r, int flag, int *A)
{
if(l == left && right == r){
cnt[rt]+=flag;
up(rt, left, right, A);
return;
}
int mid=(left + right)>>1;
if(mid >= r) update(rt<<1, left, mid, l, r, flag, A);
else if(mid < l) update(rt<<1|1, mid+1, right, l, r, flag, A);
else{
update(rt<<1, left, mid, l, mid, flag, A);
update(rt<<1|1, mid+1, right, mid+1, r, flag, A);
}
up(rt, left, right, A);
}
int binary(int key, int n, int *a)
{
int l=0, r=n-1;
while(l<=r)
{
int mid=(l+r)>>1;
if(a[mid] == key) return mid;
if(a[mid] > key) r = mid - 1;
else l = mid + 1;
}
return -1;
}
int main()
{
//freopen("in.txt","r",stdin);
int n,w=0;
while(~scanf("%d", &n))
{
ms(x,0);
ms(y,0);
ms(cnt,0);
ms(sum,0);
int u=0;
int uu=0;
int n_x=0;
int n_y=0;
for(int i=0; i<n; i++){
int x1,y1,x2,y2;
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
x[n_x++]=x1;
x[n_x++]=x2;
line_y[u].l=y1;
line_y[u].flag=1;
line_y[u].a=x1;
line_y[u++].b=x2;
line_y[u].l=y2;
line_y[u].flag=-1;
line_y[u].a=x1;
line_y[u++].b=x2;
y[n_y++]=y1;
y[n_y++]=y2;
line_x[uu].l=x1;
line_x[uu].flag=1;
line_x[uu].a=y1;
line_x[uu++].b=y2;
line_x[uu].l=x2;
line_x[uu].flag=-1;
line_x[uu].a=y1;
line_x[uu++].b=y2;
}
sort(x, x+n_x);
sort(y, y+n_y);
sort(line_y, line_y+u, cmp);
sort(line_x, line_x+uu, cmp);
int k=1;
for(int i=1; i<n_x; i++) if(x[i] != x[i-1]) x[k++] = x[i];
int kk=1;
for(int i=1; i<n_y; i++) if(y[i] != y[i-1]) y[kk++] = y[i];
int ans_y=0;
int last_y=0;
for(int i=0; i<u; i++){
int l=binary(line_y[i].a, k, x);
int r=binary(line_y[i].b, k, x);
update(1, 0, k-2, l, r-1, line_y[i].flag, x);
if(line_y[i].flag == 1){
ans_y += sum[1] - last_y;
}
else {
ans_y += abs(sum[1] - last_y);
}
last_y = sum[1];
}
ms(cnt,0);
ms(sum,0);
int ans_x=0;
int last_x=0;
for(int i=0; i<uu; i++){
int l=binary(line_x[i].a, kk, y);
int r=binary(line_x[i].b, kk, y);
update(1, 0, kk-2, l, r-1, line_x[i].flag, y);
if(line_x[i].flag == 1){
ans_x += sum[1] - last_x;
}
else {
ans_x += abs(sum[1] - last_x);
}
last_x = sum[1];
}
printf("%dn", ans_x + ans_y);
}
return 0;
}
最后
以上就是想人陪鸭子最近收集整理的关于线段树扫描线(矩阵周长并)——HDU 1828的全部内容,更多相关线段树扫描线(矩阵周长并)——HDU内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复