本文对上文(一)中最后谈到的匹配网络模型进行详述
匹配网络解决小样本学习的非参数方法基于下述两个小节所描述的组件:首先,模型中增加了记忆网络机制,给定一个小的support set
![]()
,模型为每个
![]()
定义了一个函数/分类器
![]()
,即映射:
![]()
。其次,采用一种训练模型的策略,该策略是专为从支持集中进行小样本学习而设计的。
1.模型结构
近年来,许多小组研究了使用外部记忆网络和其它使神经网络架构更“类似于计算机”的方法来增强神经网络架构。匹配网络的灵感则是来自于带有注意力机制、记忆网络和Pointer network的seq2seq模型中得到的。
在所有这些模型中,都定义了通常上来看完全可区分的神经注意力机制来访问(或读取)存储矩阵,该矩阵存储有用的信息以解决手头的任务,典型用法包括机器翻译,语音识别或问题解答。更一般化来说,搜索模型
![]()
其中
![]()
和
![]()
可以是一个序列(例如seq2seq模型中的序列),或者对是一个存储后可被读取的集合。
匹配网络设计的贡献是在设定的框架内解决小样本学习的问题。关键点是,经过训练,匹配网络能够为未观察到的类别生成其对应的标签,而无需对网络进行任何更改。更准确的说,我们是希望得到一个从带有标签的输入支持集
![]()
的K个示例(小支持集)到分类器
![]()
的映射关系。当给定一个测试样本
![]()
时,模型能够给出输出值
![]()
来表示test example的概率分布情况。
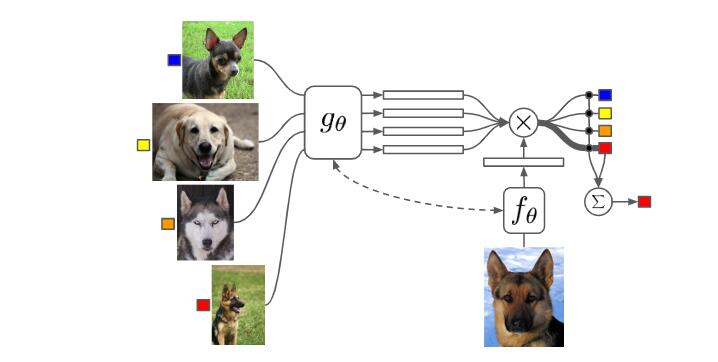
比如,在训练时给定一张猫的图片和一张狗的图片作为S,对于一张新的狗的图片,模型可以将其分类为狗;在测试时拿来一张牛的图片和一张羊的图片,又拿来一张喜羊羊的图片问模型,这个新图片是属于哪一类的,模型就会得出预测结果,即这张图属于羊。
模型的非参数化有俩部分,首先,给定(small)支持集 S,模型为每个 S 定义功能
![]()
,第二应用一个专门用于 one-shot learning 的训练策略。该文章贡献在于提出了 一个set-to-set 框架,关键点是当训练时,matching network 能够为 unobserved class 产生合理的测试标签,且不用网络做任何改变。我们希望将一个有着 k 个样本图像-标签对
![]()
小支持集映射到一个分类器
![]()
,这个分类器给定一个测试样本
![]()
,定义一个关于输出
![]()
的概率分布。我们定义映射
![]()
为
![]()
,这里
![]()
被神经网络赋值参数。这样对于给定的输入样本
![]()
和一个支持集
![]()
,预测的输出类就是
我们把映射关系
![]()
定义为
![]()
,其中
![]()
是被神经网络参数化的。
因此,当给定一个新的支持集
![]()
进行小样本时,我们只需使用
![]()
定义的参数神经网络来预测每个测试示例
![]()
的适当标签分布:
![]()
即可。
模型以其最简单的形式计算一个
![]()
上的概率:
![]()
(1)
上式中
![]()
是支持集
![]()
的输入和相应的标签分布,
![]()
是一种注意力机子,会在之后讨论。
上式本质是将一个输入的新类别描述为支持集中所有类别的一个线性组合类别。
![]()
是注意力机制,公式显示对于新的类的输出是支持集中的标签的线性组合,公式(1)组合了 核密度估计KDE(这里注意力机制可以看做是一种核密度估计) 和 KNN 方法。这里的a类似attention模型中的核函数(具体计算过程见下式),用来度量
![]()
和训练样本
![]()
的匹配度,之后通过
![]()
对于测试样本label的计算就类似于加权求和。
上式中,公式
![]()
定义了如何对测试样本编码成向量,公式
![]()
定义了如何对训练样本编码。从
![]()
是cos距离用来计算两者之间的匹配度,之后将他们做了一个softmax归一化。如果注意机制是X×X上的核,则上式类似于核密度估计器。如果选取合适的距离度量以及适当的常数,从而使得从
![]()
到
![]()
的注意力机制为0,那么上式就等价于KNN算法。
因此,上式实际上既包含KDE(核密度估计)又包含KNN。
另一种观点是,
![]()
作为一种注意力机制,而
![]()
作为与相应的key值
![]()
相绑定的值,类似于哈希表。在这种情况下,我们可以将其理解为一种特殊类型的关联记忆,在给定输入的情况下,我们“指向”支持集中的相应示例,并检索其标签。
2.注意力机制
attention kernel为cosine 距离 c
公式(1)依赖于注意力机制
![]()
的选择,该机制完全指定了分类。这种简单的形式(与常用注意力模型和内核函数有着非常紧密的关系)是在余弦距离cosine上使用softmax,即 :
![]()
。
该机制加上嵌入函数
![]()
和
![]()
以及合适的神经网络来向空间中嵌入
![]()
与
![]()
。其中f和g可以被分别参数化为用于图像任务的深度卷积网络(如VGG)或者用于nlp任务的单词嵌入等等。
3. Full Context Embeddings
模型主要的新颖之处在于重新解释一个经过充分研究的框架(带有外部记忆的神经网络)以进行小样本学习。 与度量学习密切相关,嵌入函数f和g充当特征空间的提升,从而通过等式中描述的分类函数实现最大精度。
支持集S 应该能够修改测试图像
![]()
通过函数
![]()
进行 embedding 的方式,也就是说,不是单独的对这个输入进行编码,而是也要考虑它的背景集合 S,
![]()
是特征,例如可以由 CNN 得来,K 是 LSTM 固定的 unrolling 步的大小。
关于训练集输入的处理函数
![]()
:
g的结构是一个双向LSTM,这个双向LSTM的输入序列是S中的各个样本
![]()
,
![]()
是首先对
![]()
输入到神经网络(如VGG、Inception model)进行的一个编码。采用LSTM可以全面考虑整个Support Set中所有图像的特征,并选择合适的、有代表性的部分作为
![]()
的特征。而双向LSTM可以让处在序列不同顺序的图像均能充分比较。
定义基于支持集S,对样本
![]()
的编码为
![]()
均为LSTM的输出,文章附录中给出了计算过程。
虽然函数f是编码test sample的函数,但可以预见的是当选择不同的图片作为Support Set都会影响模型的性能。如果函数f仅与test sample相关,那么support set都将影响模型性能,所以在文章中,作者提出了关于测试集输入的特殊处理函数
![]()
:
![]()
的编码结果为最后一步LSTM输出的隐状态,此处LSTM会迭代K次,即attLSTM参数中的最后一个变量。在LSTM的每一步中,输入
![]()
都是固定的,是对测试样本自身的一个编码(参考上文的
![]()
)。在这里的LSTM相当于不断地对测试样本自身进行k次迭代编码(attLSTM的K次迭代,应该是与nlp中的transformer多attention层叠加类似,不断进行非线性变换与相似性计算后,应该可以找到test真实的embedding,对于这里的K次迭代存疑,引用某知友倒的解释)。其中
![]()
将Support Set的信息融合进test sample的特征内,即函数g对f产生影响。
迭代K步的处理按照下列式子表示:
4.training strategy
task T 作为关于可能的标签集 L 的分布,标签集 L 从任务 T 中抽样,
![]()
。为了形成一个“episode”去计算梯度并且更新我们的模型,我们首先从 T 中抽样 L(例如,L 可以是标签集{猫,狗})。然后使用 L 去从支持集 S 和 batch B 中抽样(S 和 B 都是有标签的 cats 和 dogs 样本)。matching net 之后在支持集 S 的条件下最小化 B 预测标签的错误。这是一种元学习的形式,因为训练过程学习去从给定的支持集学习如何减少一个 batch 的损失。模型应用到新的类别时不需要进行微调,是因为模型学到的是一种映射的方法。Matching nets 的训练对象如下:
![]()
是模型的参数,例如之前描述过得 embedding function f & g 的参数。一个 batch 有多个任务,一个任务有一个支持集和一个测试样本,一个支持集有多个样本对,测试样本往往选取一个。
5.实验部分
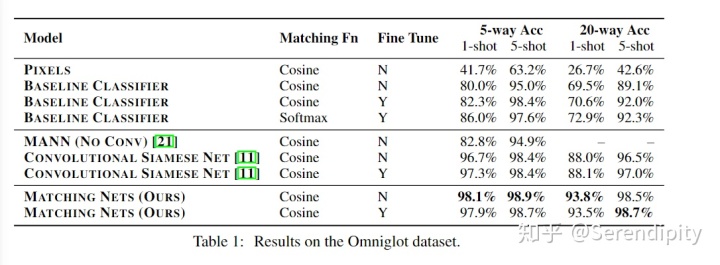
5.1.Omniglot数据集上的结果
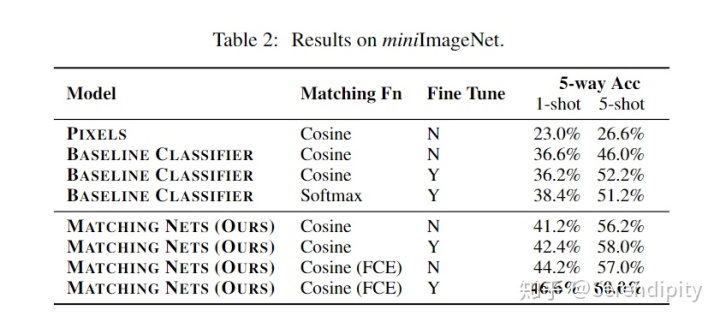
5.2.miniImageNet数据集上的结果(作者自行设定)
6.总结
本文介绍了Matching Networks(匹配网络)这种新的神经体系结构,通过其相应的训练机制,它能够在各种FSL任务中表现出比较好的性能。在这项工作中有一些关键的见解:首先,首先,如果我们在训练网络时进行FSL学习,则模型对于实际的任务
![]()
会表现更好;其次,神经网络中的非参数结构使网络更容易记住并适应相同任务中的新训练集。 将这些观察结果结合在一起便产生了匹配网络。

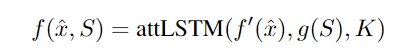
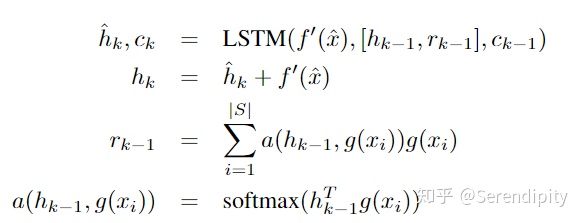
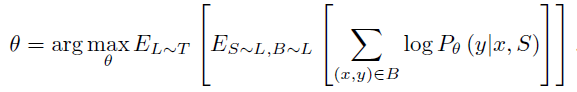






![[DeeplearningAI笔记]ML strategy_2_2训练和开发/测试数据集不匹配问题机器学习策略-不匹配的训练和开发/测试数据](https://www.shuijiaxian.com/files_image/reation/bcimg1.png)

发表评论 取消回复