Rigid Frameworks

Problem Description
Erik Demaine is a Professor in Computer Science at the Massachusetts Institute of Technology. Demaine’s research interests range throughout algorithms, from data structures for improving web searches to the geometry of understanding how proteins fold to the computational difficulty of playing games.

Maid xiaodao is learning theoretical computer science in her spare time, and recently she was fascinated by Professor Erik Demaine’s Geometric Folding Algorithms - Linkages, Origami, Polyhedra. The following problem was inspired by this book.

Recall that a graph is a collection of vertices and edges connecting the vertices, and that two vertices connected by an edge are called adjacent. Graphs can be embedded in Euclidean space by associating each vertex with a point in the Euclidean space.

⋅ A flexible graph is an embedding of a graph where it is possible to move one or more vertices continuously so that the distance between at least two nonadjacent vertices is altered while the distances between each pair of adjacent vertices is kept constant.

⋅ A rigid graph is an embedding of a graph which is not flexible. Informally, a graph is rigid if by replacing the vertices with fully rotating hinges and the edges with rods that are unbending and inelastic, no parts of the graph can be moved independently from the rest of the graph.

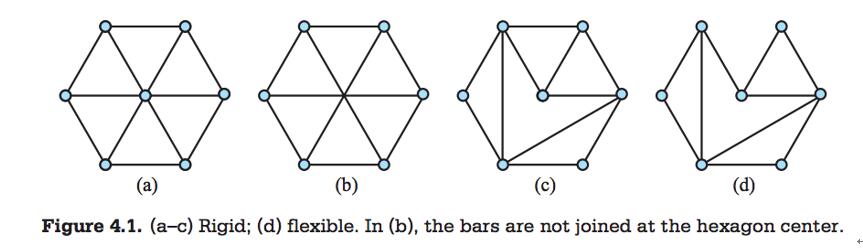
Sit down and relax, to simplify the problem, let’s only consider the planar graphs as grids. The grid graphs embedded in the Euclidean plane are not rigid, as the following animation demonstrates:

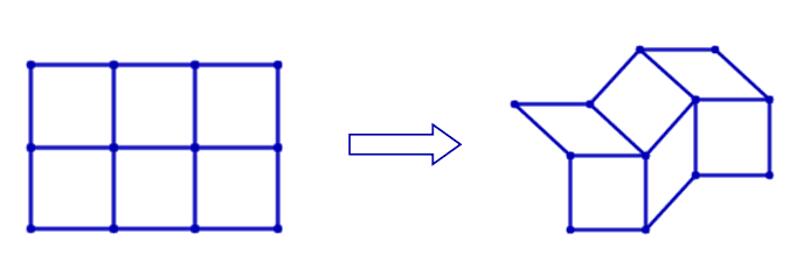
However, one can make them rigid by adding diagonal edges to the cells. For example, the following picture shows a 2 × 3 grid graph.

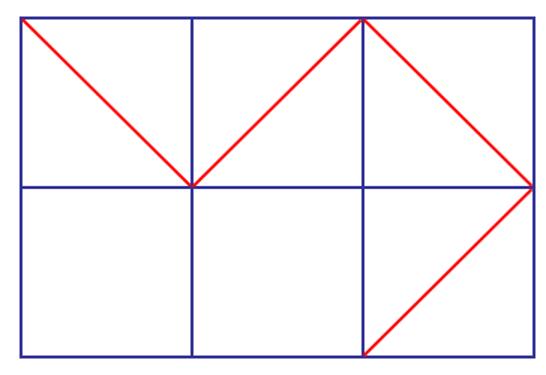
Note that you can add at most one orientation of a diagonal edge in one single cell. In fact, there are 448 ways to make a 2 × 3 grid graph rigid. And now we want to know, how many different rigid m × n grid graph with diagonal edges in total? Dear contestant, could you please find it out?

Input
There are multiple test cases. For each test case, the first line contains two integer m and n (1≤m,n≤10) represented the size of the grid graph.

Output
For each test case, output one integer number in a single line — the number of different rigid m × n grid graph with diagonal edges. The answer could be very large, output it modulo 1000000007(109+7) .

Sample Input
1 2
3 2
7 9
10 10

Sample Output
4
448
357533852
935300639

Author
HIT

Source
2016 Multi-University Training Contest 1

通过这题学习了几个简单的n点连通图计数的求法。主要都是理解好DP数组
题目大意：
这题题意也挺恶心。。给出一个n*m的格子阵，可以给每个格子主对角线或者副对角线添加线段，已知包括原有的所有线段的长度不可改变，问多少种加法可以让图稳定。
稳定的定义是无法改变形状，因为有线段长度不可变这一限制，所以添加某些线段后可以达到稳定，那么什么样的方案是稳定的呢？
——
——
——
——
——
——
——
思
——
——
——
——
考
——
——
——
——
时
——
——
——
——
间
——
——
——
——
——
——
——

这样考虑：
当第 i 行某个格子某对角线加上一条线段时，这一行中所有格子的竖边不会发生倾斜！或者说不会左右倾倒，只会出现上下移动
即
无法发生| | | | | -> / / / / /或者 -> 的情况
但可能有| | | | | -> | | |
| |的情况（=。=搞得有点抽象 大体明白我想表述的意思就好。。）

同样的，当第j列某个格子某对角线加上一条线段时，这一列中所有格子的横向边不会发生倾斜！或者说不会上下倾倒，只会出现左右倾斜

换言之，要保证任意一个格子不会扭曲，就要保证对于每一个格子，所在的行和列都至少有一个格子填上了正/副对角线

再转换一下，就变成了求n*m的二分图的连通图的个数。

通过这题发现一个好PPT
顾昱洲顾大犇的一篇，具体不贴了 名字是Graphical Enumeration

学了两个入门的
1·求n个点的有标号DAG的个数。
2·求n个点的有标号无向图的个数。
3·本题 n*m的二分图的连通图个数

1·求n个点的有标号DAG的个数。
定义 dp[n][m] 为n个点中有m个点入度为0的方案数。
此时有n-m个入度非0的点。

这样求 dp[n][m] 时可从 dp[n−m][k] 转移 即预留m个入读0的节点。
同时m个点向其余k个入度为0的点随意连接（但要保证有连接 因为要把这k个点变为入度非0的点） 同时m个点向n-m-k个点随意连接（可以不连，因为本就是入度非0）
无重复证明：为什么这样不会有重复计算呢？因为 dp[n][m] 由 ∑k=1n−mdp[n−m][k] 转移得到。
dp[n−m][k] 的含义是预留m个入度0的点，首先保证了这部分不会重复，其次 dp[n−m][k] 是之前处理出来的状态，需要保证不重复，那么现在假设 ∑k=1n−mdp[n−m][k] 这些状态都不重复，那么只要证明 dp[n][m] 由他们转移来的时候也没有重复，就可以保证转移方程合法！

首先 Cmn 选出m个入度0的点集，不重复
由他们往 k 集合还有n−m−k集合连线， (2m−1)k 往k每个点连接的组合，不可为空， 2m⋅2(n−m−k) 往(n-m-k)每个点连接的组合，可为空，因为点集k到点集(n-m-k)如果有边，一定是 {k}→{n−m−k} 这种方向 这样源状态无重复，特殊连点后也不会重复。

证毕
转移方程即为
dp[n][m]=∑k=1n−m(2m−1)k2m(n−m−k)Cmndp[n−m][k]

2·求n个点的有标号无向图的个数。
我感觉这个比较好理解。
用小容斥的方式 n个点任意连线的方案数是 2n(n−1)2
用他减掉不连通的情况，即为n个点连通的方案。
这样定义 dp[n] 表示n个点连通的方案数。
因为有编号，这样转移时假设1标号所在块为连通（自身也为连通）
这样 ∑k=1n−1dp[k] 含义定为标号1的点所在连通块k为基准。这样只要保证其余点跟这个连通块没有任何连接，其他随便连，即为当前状况的非连通方案数。
也就是 Ck−1n−1 选择跟标号1连通的其余k-1个点
2(n−k)(n−k−1)2 其余 n−k−1 个点内部任意连接。
转移方程出来了
dp[n]=2n(n−1)2总方案数−∑k=1n−1Ck−1n−12(n−k)(n−k−1)2dp[k]

3·回到此题
找n*m的二分图中连通二分图的个数。
定义 dp[i][j] 同上
同样的，计算 dp[n][m] 只要用总方案数减去不合法的即可
总方案数为 2n∗m 即共n*m条边，选择连与不练。
其中左n右m个点都有边相连为合法状态。除此外均为非法状态。
那么 2n∗m−非法状态=dp[n][m]
同上题一样，保证标号1在 dp[i][j] 中 那么 Cn−1i−1 选择 dp[i][j] 中左边其余 i−1 个点 Cmj 选择 dp[i][j] 中右边其余 j 个点 其余左边n-i个点，右边m-j个点随意组合，不与dp[i][j]中已有点连接即可。

转移方程如下：
dp[n][m]=2n∗m−∑1≤i≤n0≤j≤mCi−1n−1Cjm2(n−i)∗(m−j)dp[i][j]

需要注意的是开LL，很容易越界。
另外因为每个格子可以选择主副两种对角线，但是同效的。
也就是上面方程中2均变为3

代码如下：

#include <iostream>
#include <cmath>
#include <vector>
#include <cstdlib>
#include <cstdio>
#include <cstring>
#include <queue>
#include <stack>
#include <list>
#include <algorithm>
#include <map>
#include <set>
#define LL long long
#define Pr pair<int,int>
#define fread(ch) freopen(ch,"r",stdin)
#define fwrite(ch) freopen(ch,"w",stdout)
using namespace std;
const int INF = 0x3f3f3f3f;
const int msz = 10000;
const int mod = 1e9+7;
const double eps = 1e-8;
LL dp[11][11];
LL pre[11][11];
LL pow_m(LL a,int b)
{
LL ans = 1;
while(b)
{
if(b&1) ans = (ans*a)%mod;
b >>= 1;
a = (a*a)%mod;
}
return ans;
}
LL C(int m,int n)
{
if(m == n) return 1;
if(m == 0) return 0;
if(~pre[m][n]) return pre[m][n];
return pre[m][n] = (C(m-1,n-1)+C(m-1,n))%mod;
}
LL solve(int n,int m)
{
for(int p = 1; p <= n; ++p)
{
for(int q = 0; q <= m; ++q)
{
dp[p][q] = pow_m(3,p*q);
int cnt = 0;
for(int i = 1; i <= p; ++i)
for(int j = 0; j <= q; ++j)
{
if(i+j == p+q) continue;
cnt = (cnt+((((C(p-1,i-1)*C(q,j)*dp[i][j])%mod)*pow_m(3,(p-i)*(q-j)))%mod))%mod;
}
dp[p][q] = (((dp[p][q]-cnt)%mod)+mod)%mod;
}
}
return dp[n][m];
}
int main()
{
//fread("");
//fwrite("");
int n,m;
memset(pre,-1,sizeof(pre));
while(~scanf("%d%d",&n,&m))
{
printf("%lldn",solve(n,m));
}
return 0;
}

最后

以上就是鳗鱼世界为你收集整理的【HDU 5729】Rigid Frameworks（组合数学+DP） Rigid Frameworks 的全部内容，希望文章能够帮你解决【HDU 5729】Rigid Frameworks（组合数学+DP） Rigid Frameworks 所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。