基本操作：

判断边是否存在：

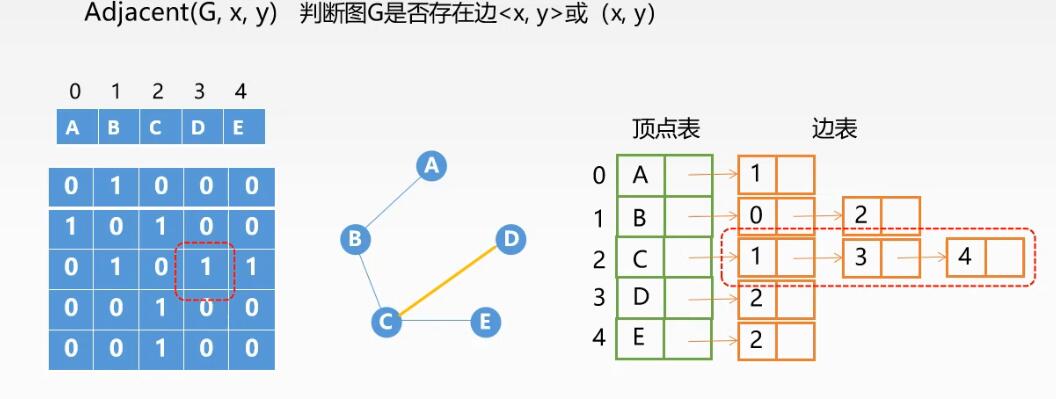
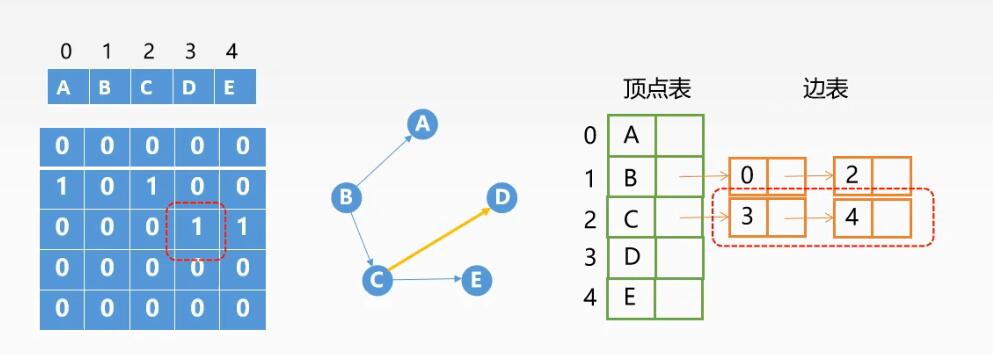
ps：
在邻接表中，要搜索某节点的整个边表才能找到是否存在边,O(1)~O(|v|)
在邻接矩阵中，只需要判断该边对应数组位置的值即可，O(1)
所以从判断是否存在边的角度看，邻接矩阵法更优

列出与某节点相邻的边：

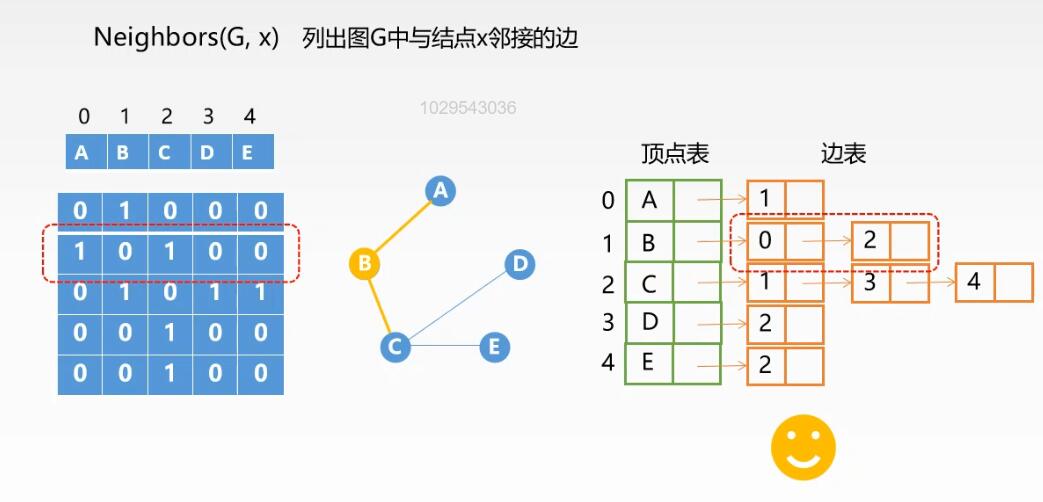
无向图：
在邻接矩阵中，只需要搜索对应行或对应列即可,O(|V|)
在邻接表中，只需要遍历该节点的边表即可,O(1)~O(|V|)
所以在无向图中， 列出与某节点相邻的边时邻接表法更优
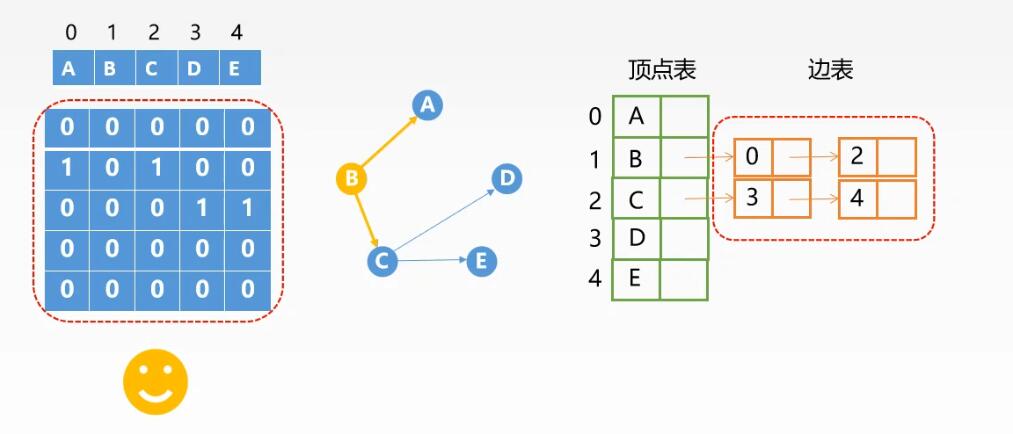
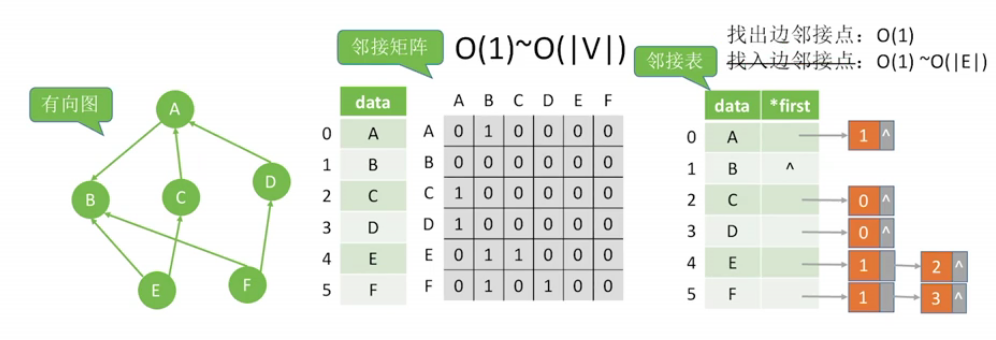
有向图：
在邻接矩阵中，只需要搜索对应行和对应列即可,O(|V|)
在邻接表中，出边很容易，但是找入边需要遍历整个边表:
1、寻找出边：O(1)~O(|V|)
2、寻找入边：O(|E|) (遍历所有的边节点)
所以在有向图中，列出与某节点相邻的边时邻接矩阵法更优(但是存储稀疏图，E比较小)

在图中插入一个顶点：

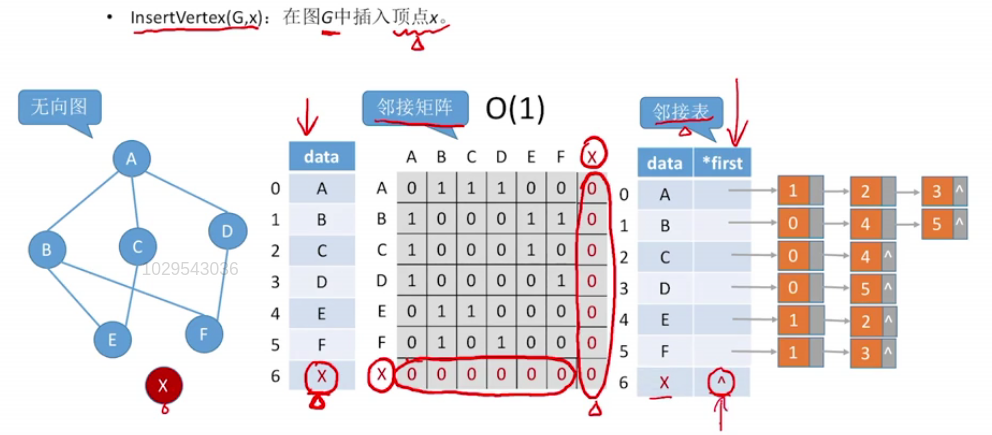
ps：
在邻接表法中，将该顶点加入到顶点表中将边的关系加入到边表中，O(1)
在邻接矩阵法中，扩充一行和一列，放置对应关系,O(1)

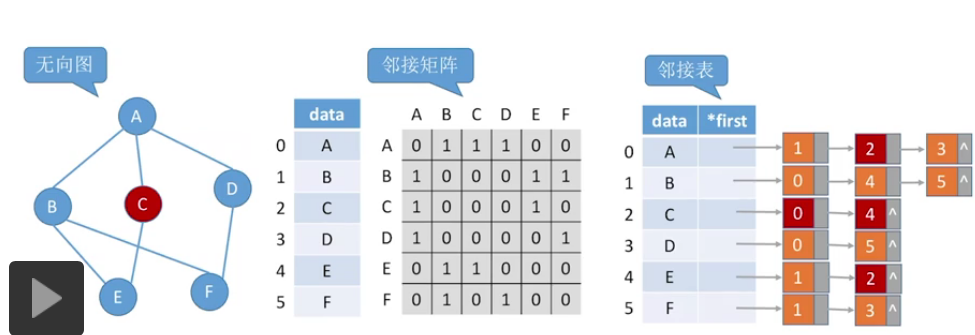
在图中删除一个顶点：

无向图：

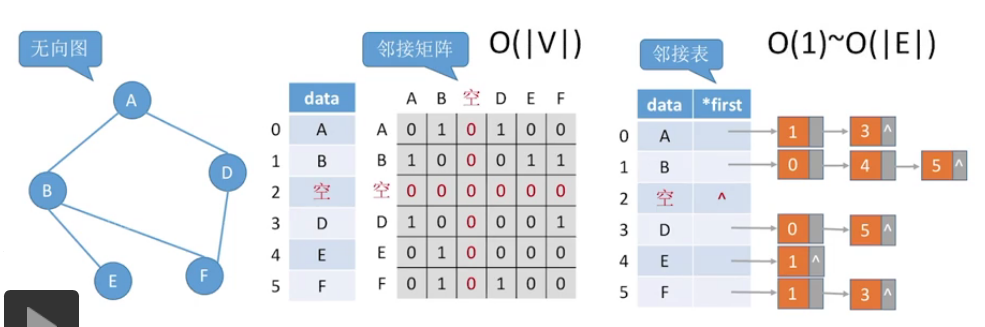
ps：
在邻接表法中，删除该节点和对应的边表即可，O(|V|)
在邻接矩阵法中，删除该顶点对应的行与列即可，有以下两种情况,O(1)~O(|E|)
1、将后续元素前移，用D覆盖C，但是会让大量元素移动，代价太大
2、将删除节点对应行列置0，在顶点结构体中设置bool变量来标记节点的空

有向图：

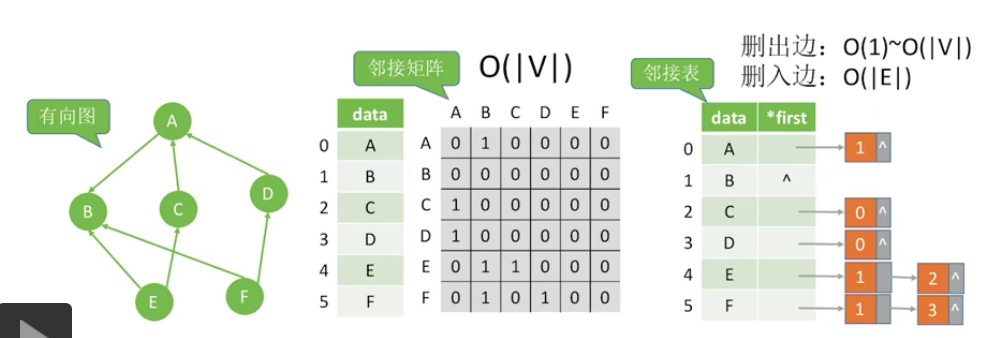
在图中添加一条边：

ps：
在邻接表法中，在俩端节点的边表添加该边，O(1)
在邻接矩阵法中，把对应的俩个矩阵值修改即可,O(1)（头插法优于尾插法，O(1)是头插法的时间复杂度，尾插法还需要遍历边表）

在图中删除一个边：

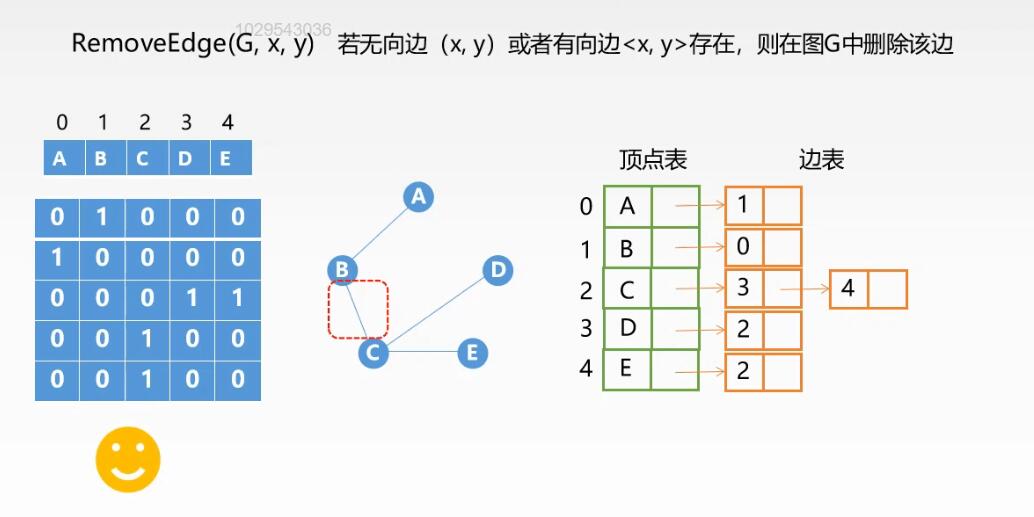
ps：
在邻接表法中，遍历整个边表找到对应的边表节点，然后删除
在邻接矩阵法中，只需要修改对应位的值即可
所以在在删除边的操作中，邻接矩阵法更优

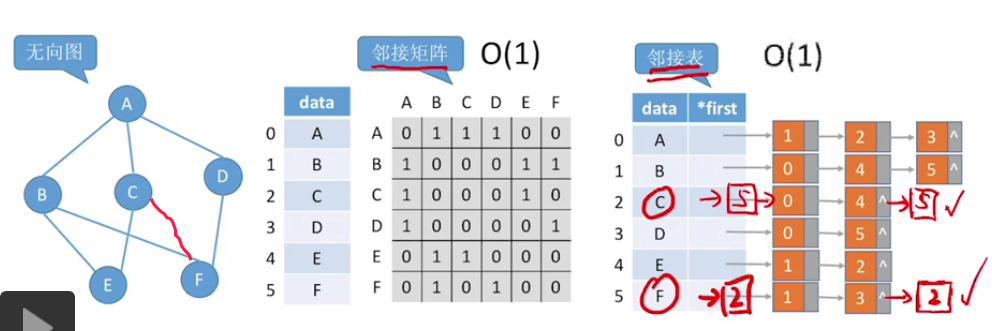
查找某顶点的第一个邻接点：

邻接矩阵：O(1)~O(|V|)
邻接表：O(1)

查找某边的权值：

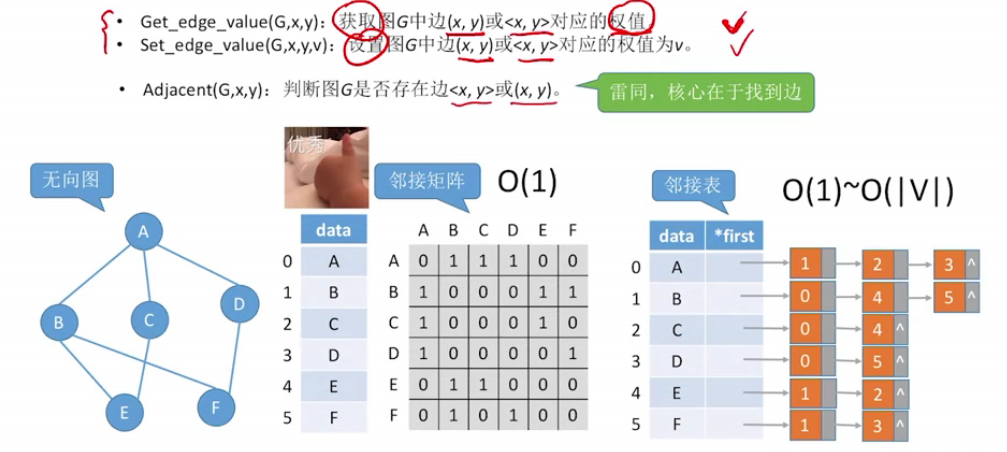
核心问题：找边
邻接矩阵：O(1)
邻接表：O(1)~O(|V|)

查找某一顶点邻接点的下一个邻接点：

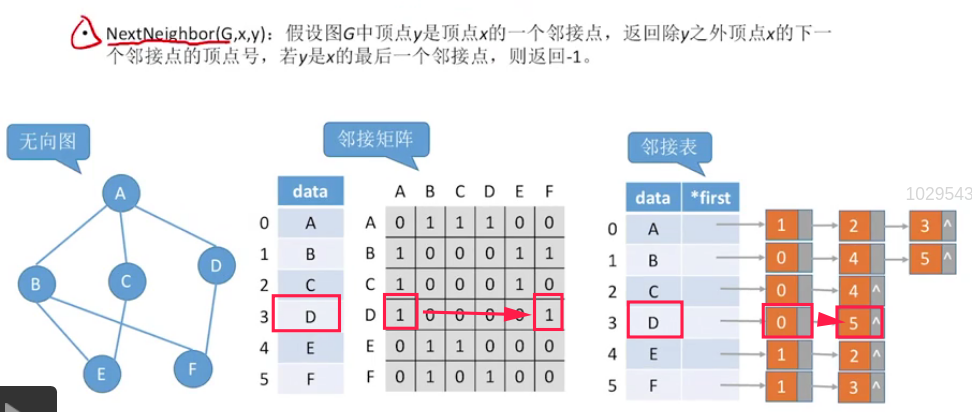
邻接矩阵：O(1)~O(|V|)
邻接表：O(1)

最后

以上就是落后曲奇为你收集整理的数据结构之图的基本操作基本操作：判断边是否存在：列出与某节点相邻的边：在图中插入一个顶点：在图中删除一个顶点：在图中添加一条边：在图中删除一个边：查找某顶点的第一个邻接点：查找某边的权值：查找某一顶点邻接点的下一个邻接点：的全部内容，希望文章能够帮你解决数据结构之图的基本操作基本操作：判断边是否存在：列出与某节点相邻的边：在图中插入一个顶点：在图中删除一个顶点：在图中添加一条边：在图中删除一个边：查找某顶点的第一个邻接点：查找某边的权值：查找某一顶点邻接点的下一个邻接点：所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。