《Attention Is All You Need》中解释是:向量的点积结果会很大,将softmax函数push到梯度很小的区域,scaled会缓解这种现象。怎么理解将sotfmax函数push到梯度很小区域?还有为什么scaled是维度的根号,不是其他的数?
Google的一般化Attention思路也是一个编码序列的方案,因此我们也可以认为它跟RNN、CNN一样,都是一个序列编码的层。
前面给出的是一般化的框架形式的描述,事实上Google给出的方案是很具体的。首先,它先把Attention的定义给了出来:
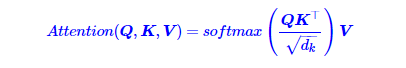
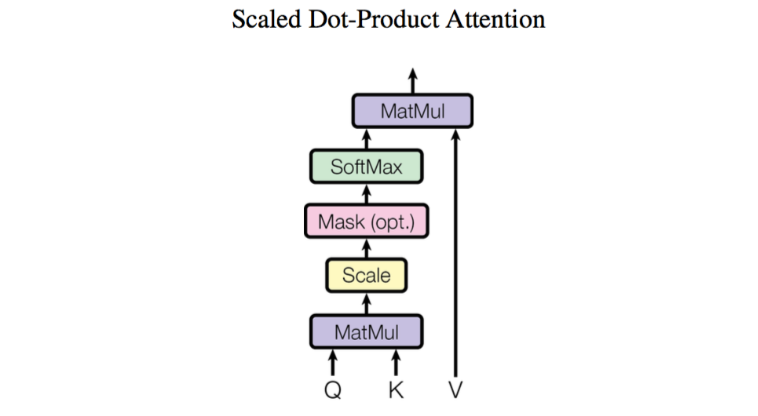
那怎么理解这种结构呢?我们不妨逐个向量来看。
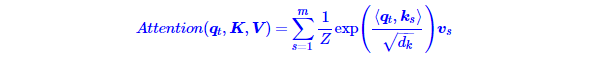
其中ZZ是归一化因子。事实上q,k,v分别是query,key,value的简写,K,V是一一对应的,它们就像是key-value的关系,那么上式的意思就是通过qt这个query,通过与各个ks内积的并softmax的方式,来得到qt与各个vsvs的相似度,然后加权求和,得到一个dv维的向量。其中因子![]() 起到调节作用,使得内积不至于太大(太大的话softmax后就非0即1了,不够“soft”了)
起到调节作用,使得内积不至于太大(太大的话softmax后就非0即1了,不够“soft”了)
以下参考自知乎:https://www.zhihu.com/question/339723385
1. 为什么比较大的输入会使得softmax的梯度变得很小?
对于一个输入向量 ![]() ,softmax函数将其映射/归一化到一个分布
,softmax函数将其映射/归一化到一个分布![]() 。在这个过程中,softmax先用一个自然底数e 将输入中的元素间差距先“拉大”,然后归一化为一个分布。假设某个输入 x中最大的的元素下标是k,如果输入的数量级变大(每个元素都很大),那么
。在这个过程中,softmax先用一个自然底数e 将输入中的元素间差距先“拉大”,然后归一化为一个分布。假设某个输入 x中最大的的元素下标是k,如果输入的数量级变大(每个元素都很大),那么![]() 会非常接近1。
会非常接近1。

我们不妨把![]() 在不同取值下,对应的的
在不同取值下,对应的的![]() 全部绘制出来。代码如下:
全部绘制出来。代码如下:
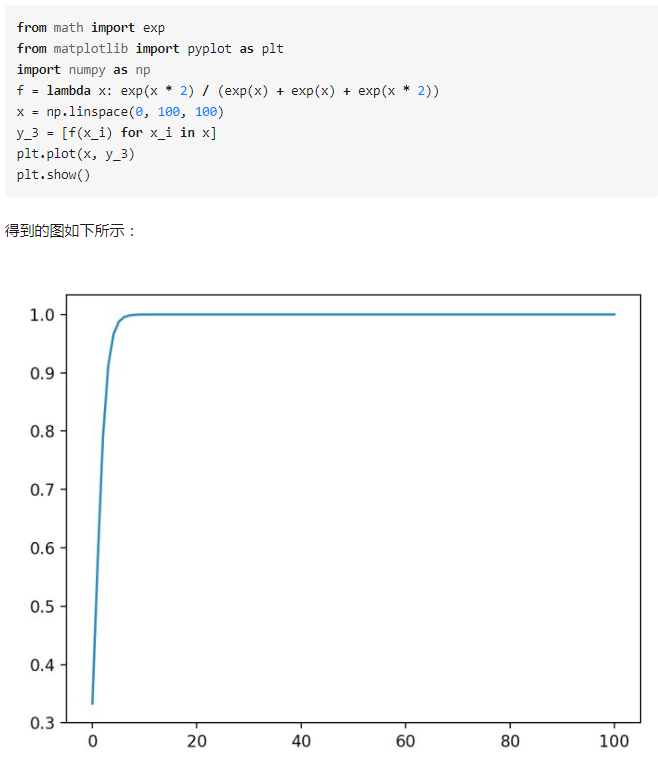
可以看到,数量级对softmax得到的分布影响非常大。在数量级较大时,softmax将几乎全部的概率分布都分配给了最大值对应的标签。
2. 维度与点积大小的关系是怎么样的,为什么使用维度的根号来放缩?
针对为什么维度会影响点积的大小,在论文的脚注中其实给出了一点解释:

假设向量 q 和 k的各个分量是互相独立的随机变量,均值是0,方差是1,那么点积 q.k 的均值是0,方差是![]() 。这里我给出一点更详细的推导:
。这里我给出一点更详细的推导:




最后
以上就是大力小蝴蝶最近收集整理的关于transformer中的attention为什么scaled?的全部内容,更多相关transformer中内容请搜索靠谱客的其他文章。








发表评论 取消回复