打劫三部曲-I

100 阅读 0 评论 66 点赞

我是靠谱客的博主暴躁中心，最近开发中收集的这篇文章主要介绍打劫三部曲-I，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

美帝最近的情况大家都懂得，作为知名IT重镇，微软和大亚麻总部所在，做事还是要讲基本原则的。参考以下fake news：据悉，暴徒本来想顺道抢Redmond的。但是在148th上被一群微软亚麻谷歌码农堵着在黑板上做这道题，做过的才能过去。如果要去富人区和富豪区还有关卡级别II/III需要通过。

https://www.lintcode.com/problem/house-robber/

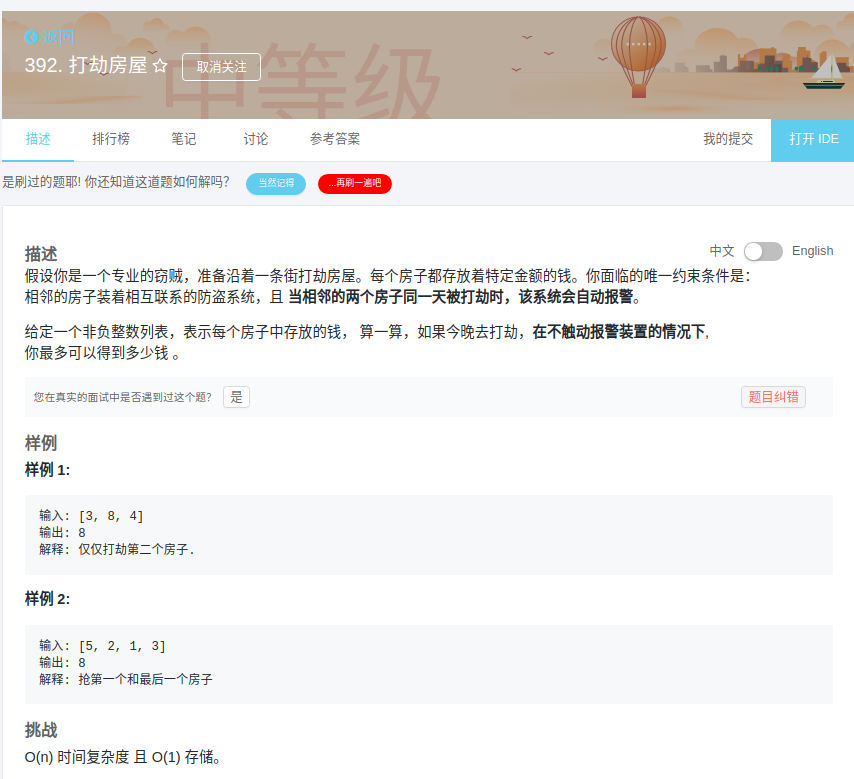
做啥都要专业，不能硬来。以多年XX经验判断，显然是动态规划的干活。累计到第i个房间能获得的最大收益取以下2种情况的的最大值。

抢了第i - 2间，最大值就是累计到第i - 2间的收益加上第i间的收益。
抢了第i - 1间，因为有报警系统，第i间不能抢，最大值就是累计到第i - 1间的收益。

动态规划的公式已经出来了，时间复杂度必然是O(n)的。对于空间复杂度，不用新开数组缓存结果，直接复用输入数组（Python没有溢出问题，Java多用两个变量），第i个元素用来存储累计到i个房间的收益，所以存储也只需要O(1)的复杂度。

实现代码如下：

# Python
class Solution:
    # @param A: a list of non-negative integers.
    # return: an integer
    def houseRobber(self, A):
        # write your code here
        if not A:
            return 0
        elif len(A) == 1:
            return A[0]
        elif len(A) == 2:
            return max(A[0], A[1])
        else:
            A[1] = max(A[0], A[1])
            for i in range(2, len(A)):
                A[i] = max(A[i] + A[i - 2], A[i - 1])
            return A[-1]

// Java版本有点小麻烦，要小心做加法溢出。所以相对Python做了些修改。
public class Solution {
    /**
     * @param A: An array of non-negative integers
     * @return: The maximum amount of money you can rob tonight
     */
    public long houseRobber(int[] A) {
        // write your code here
        if (A.length == 0) {
            return 0;
        }
        if (A.length == 1) {
            return A[0];
        }
        if (A.length == 2) {
            return Math.max(A[0], A[1]);
        }
        long ret = 0;
        long i1 = Math.max(A[0], A[1]); // i - 1
        long i2 = A[0]; // i - 2
        for (int i = 2; i < A.length; ++i) {
            ret = Math.max(i2 + (long)A[i], i1);
            i2 = i1;
            i1 = ret;
        }
        return ret;
    }
}

OK，愉快的通过了测试，开始零元大抢购！