概述
While Farmer John rebuilds his farm in an unfamiliar portion of Bovinia, Bessie is out trying some alternative jobs. In her new gig as a reporter, Bessie needs to know about programming competition results as quickly as possible. When she covers the 2016 Robot Rap Battle Tournament, she notices that all of the robots operate under deterministic algorithms. In particular, robot i will beat robot j if and only if robot i has a higher skill level than robot j. And if robot i beats robot j and robot j beats robot k, then robot i will beat robot k. Since rapping is such a subtle art, two robots can never have the same skill level.
Given the results of the rap battles in the order in which they were played, determine the minimum number of first rap battles that needed to take place before Bessie could order all of the robots by skill level.
The first line of the input consists of two integers, the number of robots n (2 ≤ n ≤ 100 000) and the number of rap battles m (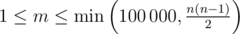
).
The next m lines describe the results of the rap battles in the order they took place. Each consists of two integers ui and vi(1 ≤ ui, vi ≤ n, ui ≠ vi), indicating that robot ui beat robot vi in the i-th rap battle. No two rap battles involve the same pair of robots.
It is guaranteed that at least one ordering of the robots satisfies all m relations.
Print the minimum k such that the ordering of the robots by skill level is uniquely defined by the first k rap battles. If there exists more than one ordering that satisfies all m relations, output -1.
4 5 2 1 1 3 2 3 4 2 4 3
4
3 2 1 2 3 2
-1
In the first sample, the robots from strongest to weakest must be (4, 2, 1, 3), which Bessie can deduce after knowing the results of the first four rap battles.
In the second sample, both (1, 3, 2) and (3, 1, 2) are possible orderings of the robots from strongest to weakest after both rap battles.
【CROC 2016 - Elimination RoundD】【二分答案orSet】Robot Rapping Results Report 最早多条边出现可以完成唯一拓扑序
#include<stdio.h>
#include<iostream>
#include<string.h>
#include<string>
#include<ctype.h>
#include<math.h>
#include<set>
#include<map>
#include<vector>
#include<queue>
#include<bitset>
#include<algorithm>
#include<time.h>
using namespace std;
void fre() { freopen("c://test//input.in", "r", stdin); freopen("c://test//output.out", "w", stdout); }
#define MS(x,y) memset(x,y,sizeof(x))
#define MC(x,y) memcpy(x,y,sizeof(x))
#define MP(x,y) make_pair(x,y)
#define ls o<<1
#define rs o<<1|1
typedef long long LL;
typedef unsigned long long UL;
typedef unsigned int UI;
template <class T1, class T2>inline void gmax(T1 &a, T2 b) { if (b>a)a = b; }
template <class T1, class T2>inline void gmin(T1 &a, T2 b) { if (b<a)a = b; }
const int N = 1e5+10, M = 0, Z = 1e9 + 7, ms63 = 0x3f3f3f3f;
int n, m;
struct A
{
int x, y;
}a[N];
vector< pair<int, int> >b[N];
int ind[N];
int s[N]; int top;
bool check(int g)
{
MS(ind, 0);
for (int i = 1; i <= g; ++i)++ind[a[i].y];
top = 0;
for (int i = 1; i <= n; ++i)if (ind[i] == 0)s[++top] = i;
int num = 0;
while (top)
{
if (top != 1)return 0;
int x = s[top--];
++num;
for (int i = b[x].size()-1; ~i; --i)if (b[x][i].second <= g)
{
int y = b[x][i].first;
if (--ind[y] == 0)s[++top] = y;
}
}
return num == n;
}
int main()
{
while (~scanf("%d%d", &n,&m))
{
for (int i = 1; i <= m; ++i)
{
scanf("%d%d", &a[i].x, &a[i].y);
b[a[i].x].push_back(MP(a[i].y, i));
}
int l = 1;
int r = m+1;
while (l < r)
{
int mid = (l + r) >> 1;
if (check(mid))r = mid;
else l = mid + 1;
}
if (l > m)l = -1;
printf("%dn", l);
}
return 0;
}
/*
【题意】
n（1e5）点m（1e5）边。
问你，当前多少条边的信息得知的时候，我们可以最早获得唯一拓扑序
【类型】
二分答案orSet
【分析】
显然，二分答案是可行的>_<
只有在当前有唯一个点可以拓扑（即栈中只有一个元素）的时候才能保证拓扑序唯一。
于是就这么快速地写完了。
【时间复杂度&&优化】
O(nlogn)
*/【CROC 2016 - Elimination RoundD】【SET做法】Robot Rapping Results Report 最早多条边出现可以完成唯一拓扑序
#include<stdio.h>
#include<iostream>
#include<string.h>
#include<string>
#include<ctype.h>
#include<math.h>
#include<set>
#include<map>
#include<vector>
#include<queue>
#include<bitset>
#include<algorithm>
#include<time.h>
using namespace std;
void fre() { freopen("c://test//input.in", "r", stdin); freopen("c://test//output.out", "w", stdout); }
#define MS(x,y) memset(x,y,sizeof(x))
#define MC(x,y) memcpy(x,y,sizeof(x))
#define MP(x,y) make_pair(x,y)
#define ls o<<1
#define rs o<<1|1
typedef long long LL;
typedef unsigned long long UL;
typedef unsigned int UI;
template <class T1, class T2>inline void gmax(T1 &a, T2 b) { if (b>a)a = b; }
template <class T1, class T2>inline void gmin(T1 &a, T2 b) { if (b<a)a = b; }
const int N = 1e5 + 10, M = 0, Z = 1e9 + 7, ms63 = 0x3f3f3f3f;
int n, m;
struct A
{
int x, y;
}a[N];
int ind[N];
bool e[N];
vector<int>b[N];
//注意，当我们定义了set的比较规则的时候，在比较规则中相等的值set只会保留一个
set<pair<int,int>>sot;
int solve()
{
MS(e, 0);
MS(ind, 0);
sot.clear();
for (int i = 1; i <= n; ++i)sot.insert(MP(0,i)), b[i].clear();
int num = 0;
for (int i = 1; i <= m; ++i)
{
int x = a[i].x; int y = a[i].y;
if (e[x])continue;
b[x].push_back(y);
sot.erase(MP(ind[y]++,y));
sot.insert(MP(ind[y], y));
while (sot.size() == 1 || (++sot.begin())->first > 0)
{
int x = sot.begin()->second;
e[x] = 1;
sot.erase(sot.begin());
for (int j = b[x].size() - 1; ~j; --j)
{
int y = b[x][j];
sot.erase(MP(ind[y]--, y));
sot.insert(MP(ind[y], y));
}
if (++num == n)return i;
}
}
return -1;
}
int main()
{
while (~scanf("%d%d", &n, &m))
{
for (int i = 1; i <= m; ++i)scanf("%d%d", &a[i].x, &a[i].y);
printf("%dn", solve());
}
return 0;
}
/*
【题意】
n（1e5）点m（1e5）边。
问你，当前多少条边的信息得知的时候，我们可以最早获得唯一拓扑序
【类型】
二分答案orSet
【分析】
显然，二分答案是可行的>_<
只有在当前有唯一个点可以拓扑（即栈中只有一个元素）的时候才能保证拓扑序唯一。
于是就这么快速地写完了。
SET做法稍微麻烦一点，但是可以即时处理
【时间复杂度&&优化】
O(nlogn)
*/最后
以上就是端庄电话为你收集整理的【CROC 2016 - Elimination RoundD】【二分答案orSet】Robot Rapping Results Report 最早多条边出现可以完成唯一拓扑序的全部内容，希望文章能够帮你解决【CROC 2016 - Elimination RoundD】【二分答案orSet】Robot Rapping Results Report 最早多条边出现可以完成唯一拓扑序所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复