Codeforces Round #365 (Div. 2) A（暴力） B（数学技巧） C（二分）D（线段树+离散）E（乘除法DP+约数分解+map映射）

69 阅读 0 评论 46 点赞

我是靠谱客的博主如意斑马，最近开发中收集的这篇文章主要介绍Codeforces Round #365 (Div. 2) A（暴力） B（数学技巧） C（二分）D（线段树+离散）E（乘除法DP+约数分解+map映射），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

传送门：A. Mishka and Game

暴力记录两人赢的次数，最后将次数再比较一次即可

#include <bits/stdc++.h>
using  namespace  std;
int n;

int  main(){
  int c1=0,c2=0;
  cin>>n;
  for(int i=0; i<n; i++){
    int x,y;
    cin>>x>>y;
    if(x>y)c1++;
    if(x<y)c2++;
  }
  if(c1==c2)puts("Friendship is magic!^^");
  else if(c1>c2)puts("Mishka");
  else puts("Chris");
  return 0;
}

传送门： B. Mishka and trip

题意：
n个城市(记为1~n)中有k个省会城市

下标相邻的两个城市之间有一条路,省会城市与除本城市外的其他城市均有一条路,两城市间最多只有一条直接相邻的路

每条路的价值为连接两城市的价值之积,比如道路连接城市i和j,那么该路的价值为c[i]*c[j]

问所有路的价值之和为多少

思路：

显然,此题的求解必须做到不重不漏才能正确，那么如何做到不重不漏呢?

首先,我们要学会如何将公式化简：对于从城市i出发的所有道路,假设有k条,它们通向城市p1,p2,……,pk

那么这些路的价值之和为

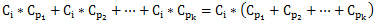
可见,我们可以先将价值之和处理出来

因为省会城市到其他城市均有路,且包含相邻下标城市之间的路

故我们可以优先处理省会城市，然后每处理一个省会城市,就将该城市的价值标0,这样就不会重复计算同一条路的价值

最终再把非省会城市且还没有处理的路算上就OK了

复杂度O(n)

#include <bits/stdc++.h>
#define ll __int64
using  namespace  std;
const int N=1e5+10;
int  n,k;
int a[N];
ll sum,ans;

int  main(){
  scanf("%d %d",&n,&k);
  for(int i=1; i<=n; i++){
      scanf("%d",&a[i]);
      sum+=a[i];
  }
  while(k--){
    int id;
    scanf("%d",&id);
    sum-=a[id];
    ans+=sum*a[id];
    a[id]=0;
  }
  a[0]=a[n];
  for(int i=1; i<=n; i++){
    ans+=a[i]*a[i-1];
  }
  printf("%I64dn",ans);
  return 0;
}

传送门： C. Chris and Road

题意：

一个凸多边形汽车,朝x轴负方向以速度v移动(意味着该凸多边形的每个顶点只有横坐标x会改变)

一个行人想从(0,0)到达(0,w),该行人可以以不超过u的任意速度在y轴上运动,可停止

问行人在不被汽车撞到的情况下,最快需要多少时间到达(0,w)

思路：

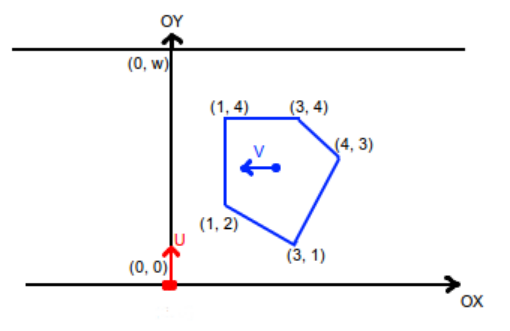
行人要到达(0,w)有两种情况:

①在汽车到达y轴前,行人已经经过碰撞点

这种情况下,行人可以全速前进,需要的时间为w/u

那么如何判断会不会被撞上呢?

因为点落在多边形内才算被撞上

那么枚举多边形的每个点(xi,yi),当行人以速度u到达yi时,此时该点已经经过y轴,说明行人无法在汽车到达y轴前经过碰撞点

即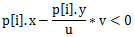

②在汽车离开y轴后,行人经碰撞点到达(0,w)

因为行人到每个点的时间是不一样的,你在某个时间不会碰到多边形的某个点,但不能保证在下一个时间不会碰上多边形的另一个点

所以,我们采取二分时间判可行性,即二分行人需要等待汽车行驶的时间t

判可行性还是枚举多边形的每个点

若存在某点满足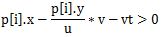,那么该时间t是不可行的

大致二分100次精度就差不多了

复杂度：O（100*n）

#include <bits/stdc++.h>
#define pr(x) cout << #x << "= " << x << "  "
#define pl(x) cout << #x << "= " << x << endl;
#define Memset(x, a) memset(x, a, sizeof(x))
#define ll __int64
#define eps 1e-9
using  namespace  std;
const int N=10005;
struct  point{
  double x,y;
}p[N];
int n;
double w,v,u;

int judge(double x){
  if(x>eps)return 1;
  if(x<-eps)return -1;
  return 0;
}

bool  judge_before(){
  for(int i=0; i<n; i++){
    if(judge(u*p[i].x-p[i].y*v)<0)return false;
  }
  return true;
}

bool judge_after(double t){
  for(int i=0; i<n; i++){
    if(judge(u*p[i].x-p[i].y*v-u*v*t)>0)return  false;
  }
  return true;
}

int  main(){
  scanf("%d%lf%lf%lf",&n,&w,&v,&u);
  for(int i=0; i<n; i++){
    scanf("%lf%lf",&p[i].x,&p[i].y);
  }
  /*车到达y轴前,路人能到达(0,w)*/ 
  if(judge_before()){
    printf("%.10lfn",w/u);
    return 0;
  }
  /*车离开y轴后,路人能到达(0,w)*/ 
  double  l=0,r=1e9,mid;
  for(int i=0; i<100; i++){
    mid=(l+r)/2;
    if(judge_after(mid))r=mid;
    else l=mid;
  }
  printf("%.10lfn",w/u+(l+r)/2);
  return 0;
}