【论文精读】Constructing Image Panoramas using Dual-Homography Warping

论文下载地址

摘要

本文描述了一种构建全景场景无缝图像拼接的方法，该全景场景包含两个主要平面：一个遥远的后平面和一个从摄像机位置向外扫掠的地平面。当相机围绕其光学中心小心旋转时，这种类型的全景图可以缝合，但这样理想的场景捕捉很难正确执行。现有技术使用每个图像的单一单应性来执行对齐，然后通过接缝切割或图像混合来隐藏不可避免的对齐伪影。在本文中，我们演示了如何使用每个图像的两个单应性来生成更无缝的图像。具体来说，我们的方法在对齐过程中混合单应性以执行非线性扭曲。一旦对图像进行几何缝合，它们将被进一步处理以混合接缝，并减少由于非线性扭曲而产生的曲线视觉伪影。正如在我们的论文中所展示的，我们的程序能够为当前最先进的技术失败的这种类型的场景生成结果。

一、介绍

尽管图像拼接近年来受到了广泛的关注，但它仍然是一个具有挑战性的问题。最麻烦的问题是，关于输入的假设，例如图像是一个遥远的场景，或者图像是通过围绕其投影中心旋转相机捕获的，很少得到满足。这导致了缝合图像的错位。这些错位通过后期处理技术(如图像混合或接缝切割)被隐藏起来，并获得不同程度的成功，通常生成的马赛克在快速一瞥中看似无缝，但在更仔细的检查中却暴露出断裂和撕裂。
我们关注一种常见类型的场景，这种场景对于现有方法来说特别麻烦：一个场景包含一个远平面和一个从摄影机位置向外扫掠的地平面。如图1所示，这种场景在需要全景成像的旅游景点很常见。现有的方法依赖于估计每个图像的单平面透视变换（单应）来对齐场景。然而，当输入图像违反成像假设时，单个单应不能对齐图像内容。现在唯一的选择是尝试通过后处理隐藏偏差。

在本文中，我们描述了如何在后处理阶段解决这种全景场景，重点是如何改进图像对齐。这是通过估计每个图像对的两个单应性并混合这些单应性来对齐图像来实现的。正如我们的结果所证明的，这种方法可以产生比使用当前最先进的方法获得的结果更无缝的结果，这些方法依赖于每个图像对的单个单应性。鉴于我们的场景有两个主要平面，这似乎是一个直截了当的想法，但我们的论文中提出了几个问题，必须考虑这些问题才能使这种方法起作用。这些问题包括从匹配点估计双单应性，混合单应性的权重，扩展非线性扭曲以连接相邻图像，以及后处理以混合图像并减少非线性扭曲引入的不希望的曲线伪影。
本文的剩余部分组织如下：第2节讨论了相关工作；第3节描述了我们对输入图像对的双单应估计和混合，以及对多图像拼接的扩展；第4节描述了减少视觉接缝和矫正曲线伪影的后处理程序；第5节展示了使用我们的方法获得的结果，第6节对我们的工作进行了讨论和总结。

二、相关工作

图像拼接是计算机视觉领域的一个研究热点（代表性著作包括[18,19,6,7,9,23]）；有关优秀的调查，请参见[22]。此外，还有一些免费软件和商业软件可用于执行图像拼接，特别是：AutoStitch[1]、Microsoft的图像合成编辑器[2]和Adobe的Photoshop CS5[3]拼接功能。
这些方法都是在假设输入图像包含很少或没有视差的情况下工作的，这意味着场景距离相机足够远，可以认为是平面的，或者图像是从围绕其投影中心小心旋转的相机拍摄的。在此假设下，图像可以通过透视平面（即单应）变换对齐[11]。这些现有技术在这些条件下工作得非常好，但当违反成像假设时，很快就会出现错位伪影。当出现这种情况时，算法会尝试使用图像混合（例如[7,12]）或接缝切割[4]来隐藏错位。
修复由于相机模型冲突、传播错误或视差造成的校准偏差(有时称为去伪影[21])的想法并不新鲜。各种方法使用局部对准匹配[21]和散点插值[8]，或其他非线性扭曲方法[13]来纠正重叠区域的问题。然而，这些方法假设输入图像可以使用初始全局对齐来合理地对齐，并且偏移相对较小。具有更灵活成像模型的方法包括ReliefMosaic[15]，它使用密集匹配来执行视图变形，以产生可渲染到拼接的2.5D光场。该方法需要一个具有足够纹理的图像场景来估计准密集的图像视差。使用流形镶嵌[20]的工作也允许一个通用的成像框架，但需要密集的输入以条形相机的方式选择图像条。我们的工作，它的场景类型更受限制，介于传统的镶嵌与强烈的成像假设之间，这些一般方法需要密集匹配或密集视频输入。就我们所知，以前还没有人使用过双单应的概念。

三、双单应性对齐

我们首先描述如何计算一对重叠图像的两个单应性，以及如何使用双单应性执行非线性对齐。然后，我们将描述如何将此扭曲扩展到拼接中的相邻图像。为了简单起见，我们假设全景图中的每个图像最多有两个重叠区域，且图像位于其任一边界上。

3.1 对偶单应性估计

我们的方法使用两个单应性Hg和Hd的混合来模拟全景图中两个重叠图像之间的关系，表示为:

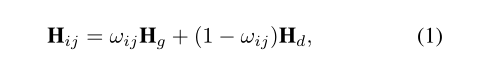
其中Hg和Hd分别表示地平面和远处平面的单应性，ωij是每个像素的权重，控制每个单应在像素位置(i, j)的贡献。
与其他拼接技术一样，我们的方法从输入图像之间匹配的一组对应点开始。我们使用SIFT特征[17]来建立对应关系，就像在[7]中所做的那样。由于我们计算每个图像对的两个单应，我们的第一步是根据图像中的空间位置将对应分为Gg和Gd两组。这是使用K-means聚类完成的，2D种子点取为:

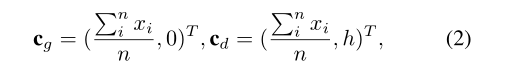
其中h为输入图像的高度。选择这些种子点是为了确保最终的簇是朝向图像的顶部和底部的，因为我们预计远处的平面和地平面很可能分别位于图像的顶部和底部。我们注意到，这个初始步骤不需要太精确，因为在单应性估计过程中会丢弃离群值。
将特征点分组后，使用随机样本一致性（RANSAC）[10]稳健地估计每组的单应性。在每个试验中，我们选择四个匹配的特征点来计算单应性。如果一致性达到95%，则估计的单应Hg和Hd被视为其相应特征组的变换。执行RANSAC后，去除离群点SIFT特征，形成新组Gg’和Gd’。
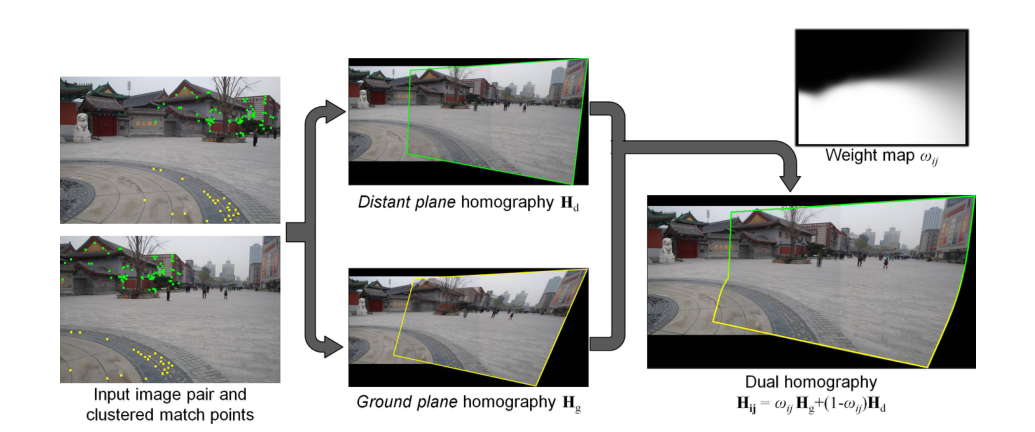
产生的两个单应性可以部分对齐图像，如图2所示。现在的目标是为每个像素位置pij分配一个权重，以确定每个单应使用多少。一个很自然的选择是基于空间邻近度来衡量扭曲，即:

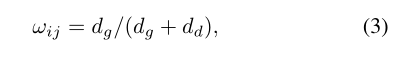
其中dg和dd分别为Gg’和Gd’集合中距离最近的特征点||·||−12的距离。图2显示了这个加权映射的一个示例，以及这种加权双单应弯曲的结果。

3.2 拓展到多图像

与可以轻松将多个单应性连接成单个矩阵的单一单应性方法不同，我们的非线性翘曲需要更加小心。图3用来帮助说明使用我们希望映射到虚拟镶嵌图像平面iv的三个重叠图像I0、I1和I2的拼接过程。I0用作镶嵌的根图像，没有发生扭曲。

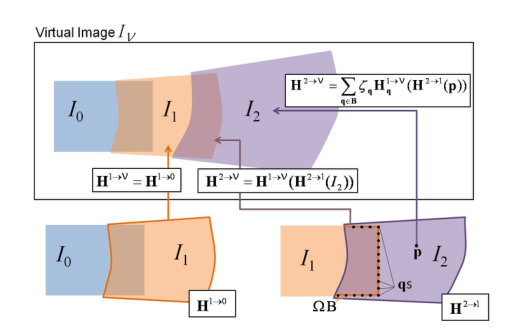
用于将I1映射到I0的第一个双单应性表示为H1→0，为了清晰起见，去掉了下标ij。这种双单应性的计算方法如前所述，它是将I1置于虚像中所需要的唯一映射:即H1→V=H1→0。
现在的任务是添加另一个双单应性对，H2→V，将 I2 映射到虚像平面中的 I1。这是通过首先计算双单应，H2→1，使I2与I1对齐来实现的。这是按照前一节的描述进行计算的。注意，这个估计是不知道I1和I0之间的关系的。而在虚图像IV中，图像I1表示为H1→0(I1)。因此，在I2和I1之间的重叠区域，我们可以通过H1→0(H2→1(I2))将I2与虚像联系起来。
现在的问题是我们如何处理I2和I1的非重叠区域。与单应性方法不同，单应性之间的映射可以应用于重叠区域之外的点，我们的扭曲函数H1→0对I1之外的点没有定义。为了“实际上扩展”H1→0的范围，我们使用了H1→V边界点的加权混合，结果是: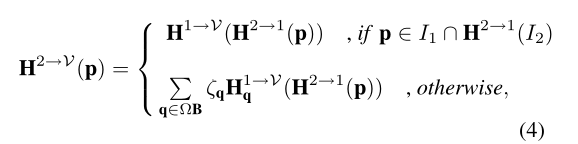
ΩB是I1和I2重叠的边界。ζq= 1/||H2→1§−q||由ΩB上点p到所有边界点q的欧氏距离计算得到。注意，这些权重被规范化为Σζq= 1。
虽然仅使用三个图像说明了此过程，但直接从等式4推导递归表达式以连接更多图像是很简单的。

四、拼接后处理

本节描述了两种后期处理技术，接缝混合和矫直，用于增强我们最终结果的美观外观。接缝混合的目的是减少重叠图像之间的可见接缝。内容感知矫直是我们的镶嵌程序的独特之处，用于减少由双单应翘曲引起的曲线效应。

4.1 接缝混合

有两种主要方法可以减少重叠区域中的可见接缝。第一种是混合整个重叠区域，此类技术包括羽化技术[22]，多波段混合[7]和梯度域缝合[14]。第二个是在图像之间执行图像剪切[4]。我们发现两者的结合产生了最好的结果。
切缝： 为了计算两个图像之间的最佳接缝，对于最终全景图结果中的每个像素p，其强度应该从一个扭曲的源图像映射。该分割问题被描述为一个二进制标记马尔可夫随机场（MRF），其中每个像素p被分配一个标签l∈ {0,1}（有关MRF的详细信息，请参见[16]）。为了求解MRF，将以下能量项最小化，以找到最佳像素标签：

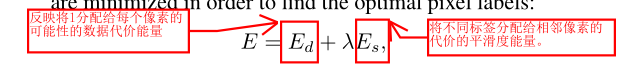
其中Ed是反映将l分配给每个像素的可能性的数据代价能量，Es是表示将不同标签分配给相邻像素的代价的平滑度能量。我们将权重λ固定为2。
按照[4]中的公式，数据成本定义为该位置像素的梯度：

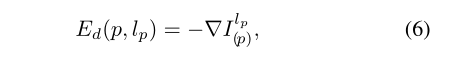
其中，二进制标签lp决定使用两个重叠图像之间的哪个梯度。两个像素p和q之间的平滑度成本定义为：

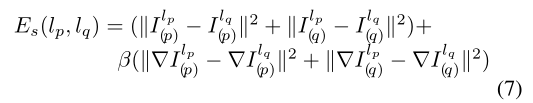
表示每对相邻像素之间的不连续性。我们看到，如果lp=lq，平滑度代价为0，而如果lp≠lq，平滑度代价是图像lp和lq中对应点的强度和梯度差。图割优化用于将标签分配给我们的MRF[5]。

混合： 虽然接缝切割产生的图像没有重叠，但颜色不连续可能仍然很明显。为了减少这种情况，我们将接缝扩展16个像素，并对扩展接缝中的像素执行简单的线性alpha混合[21]，如图4所示。我们发现，这种接缝切割和局部接缝混合的组合方法比接缝切割或单独混合整个重叠区域产生更好的效果。

4.2 全局矫直

单应性的线性插值使图像以二次形式弯曲。这可能会引入一种弯曲的效果，而这种效果在美学上可能并不吸引最终的结果。
为了改善这种效果，我们采用了一种类似于[24,25]中使用的内容感知扭曲方法。特别地，我们最终的虚图像IV被细分成一个多边形网格，其中每个多边形Q要么是一个四边形，要么是一个三角形。我们的网格是通过将输入图像镶嵌到四边形中来计算的，然后确定这些四边形如何扭曲到虚拟图像中，IV。输入图像之间的重叠区域使用三角形压缩在一起。图5显示了这个多边形网格的一个例子。

每个多边形由顶点vi组成，这些顶点可以变形为一组新的多边形Q’，具有以下两种变形能量：

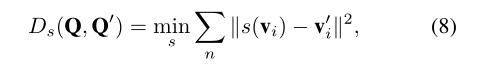
其中vi’是vi的目标翘曲位置，s（·）是一个类似的变换函数，具有一般形式：

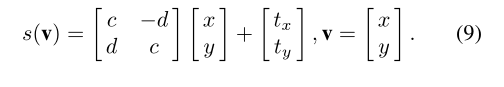
该能量试图约束所有点vi上的变形，使得多边形Q仅经历相似性变换。
另一种失真能量是根据[7]中观察到的，人们在拍摄全景图像时很少会相对于地平线扭曲相机。因此，我们给垂直边E上的每个点对v1和v2一个弯曲代价能量，定义如下:

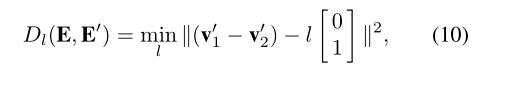
其中l是任意比例因子。该能量会更多地约束源图像中的所有垂直边，以在最终结果中保持垂直位置。结合这两种能量，我们可以得到拉直的结果，即点集V’={vi’}，它使以下能量最小化：

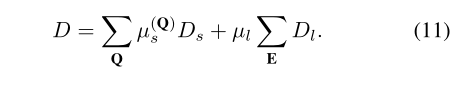
这里，重量µ（Q）s是允许该变形具有柔性的因素。该权重由每个多边形中包含的基础图像内容Q确定，定义为：

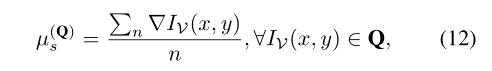
其中∇IV是多边形内的图像渐变。该方法对图像能量较高的多边形进行加权，以抵抗变形，而对图像能量较低的多边形进行变形。为了加强垂直边的约束，我们给出了较大的权重µl，相当于max{µ(Q)s}的20倍，来强制直线。
该方法类似于[24,25]提出的内容感知图像大小调整方法，但是，我们以完全不同的方式使用它，利用其使用等式11线性化网格的能力。如[25]中所述，该系统使用过度确定的线性解算器直接计算。图5显示了此矫直程序前后的结果示例。
虽然非线性矫直旨在修复双单应性扭曲引入的伪影，但它有时会在图像内容上引入明显的弯曲。因此，我们有一个简单的UI，允许用户指定形状无法更改的图像区域，如图6所示。这可以通过增加用户指定区域内多边形的µ（Q）s来实现。图6显示了如何在此矫直过程中使用用户标记保护区域的示例。

五、结果

我们的结果与三种最先进的软件进行了比较：AutoStitch[1]、Photoshop CS5的镶嵌功能[3]和Microsoft的ICE[2]。AutoStitch[1]基于[6]中的工作，而Photoshop和ICE似乎结合了[6]和接缝切割[4]的元素。所有这些技术都利用单应对齐。图像是在符合我们目标场景描述的位置拍摄的。在对这些场景进行成像时，我们故意以弧形方式移动摄影机，以违反输入图像的公共投影中心假设。
图8和图9显示了我们的算法在包含五幅输入图像的全景序列上的结果。这些结果与AutoStitch和Photoshop CS5进行了比较。虽然所有的结果乍一看都很好，但我们强调了几个值得注意的区域，其中AutoStitch和Photoshop的结果显示了严重的偏差。然而，我们的结果在这些地区仍然是天衣无缝的。Photoshop产生的结果中的不对齐通常最难检测，因为它们使用接缝切割将图像缝合在一起。虽然此处未显示，但ICE产生的结果与Photoshop在这些示例中的结果相似，只是接缝稍微明显一些。对于图8中的示例，使用了Section4中显示的用户标记。
图10显示了将我们的方法与所有三种软件进行比较的结果。同样，乍一看，每种方法都表现得很好，通过仔细检查，我们可以看到由于结果中未显示的对齐问题而产生的工件。请注意，大多数错误发生在全景图像的底部。这意味着基于单应的方法正在使用远处平面区域中的点来计算其单应，从而导致地平面区域中的失准。我们还注意到，与Photoshop CS5的结果相比，输入图像的颜色平衡不足有时是显而易见的。
当场景包含不属于地平面或远平面的相对较大的结构时，我们的方法失败。在这种情况下，将发生视差效应，因为涉及两个以上的单应性。图7显示了此故障情况的示例。

我们方法的运行时间大约为单应性估计阶段5 ~ 10秒，接缝切割阶段5 ~ 10秒，矫直阶段5 ~ 10秒(对于典型的5张图像输入)。与autostitch和Photoshop的10 ~ 15秒左右的其他软件相比，我们的方法需要更长的时间来处理，主要是由于复杂的翘曲过程。

六、讨论和总结

我们已经演示了如何使用双单应变形来对齐包含主要远平面和地平面的全景场景的图像。虽然这种方法在处理多幅图像时比单应方法需要更多的工作，但额外的处理被生成无缝图像的能力所抵消。结合标准的后处理方法（接缝切割和混合），再加上矫直程序，我们的方法可以产生在当前最先进的方法中没有断裂和撕裂的结果。
与之前的工作不同，我们的方法不基于任何特定的相机模型，因此对于最终全景中的光传输没有物理意义。然而，当违反成像假设时，先前的工作被迫隐藏未对准伪影，而我们通过放松成像模型来隐藏错误。本质上，我们的双单应方法代表了一种在非理想成像条件下对齐全景图像的有效方法。
我们的工作的自然延伸是考虑两个以上的平面。此扩展可以快速地推动自身实现完整的3D场景理解，并最终从运动设置中估计形状中的代理几何体。确定要估计的最小平面数以在给定场景中保持无缝全景是未来工作的一个有趣途径。

最后

以上就是幽默蜻蜓为你收集整理的【论文精读】Constructing Image Panoramas using Dual-Homography Warping的全部内容，希望文章能够帮你解决【论文精读】Constructing Image Panoramas using Dual-Homography Warping所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。