目录
序
插入排序
直接插入排序
希尔排序
选择排序
直接选择排序
堆排序
交换排序
冒泡排序
快速排序
归并排序
非比较算法
计数排序
时间复杂度
序
排序:就是将一组杂乱无章的数据按照一定的规律(升序或降序)组织起
来。
排序码:通常数据元素有多个属性域,其中有一个属性域可用来区分元
素,作为排序依据,该域即为排序码。
按照主排序码进行排序,排序的结果是唯一的。
按照次排序码进行排序,排序的结果可能是不唯一的
稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面。
不稳定:如果a原本在b的前面,而a=b,排序之后 a 可能会出现在 b 的后面。
时间复杂度:对排序数据的总的操作次数。反映当n变化时,操作次数呈现什么规律。
空间复杂度:是指算法在计算机内执行时所需存储空间的度量,它也是数据规模n的函数。
插入排序
直接插入排序
插入排序(Insertion-Sort)的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入
- 从第一个元素开始,该元素可以认为已经被排序;
- 取出下一个元素,在已经排序的元素序列中从后向前扫描;
- 如果该元素(已排序)大于新元素,将该元素移到下一位置;
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置;
- 将新元素插入到该位置后;
- 重复步骤2~5。
#include<stdio.h>
#include<string.h>
void InsertionSort(int* arr,int len)
{
int i ,j;
for (i = 1;i <= len;i++)
{
j = i;
while (j--)
{
if (arr[j - 1] > arr[j])
{
int temp = arr[j - 1];
arr[j - 1] = arr[j];
arr[j] = temp;
}
else
{
break;//小于退出while循环提高效率
}
}
}
}
int main()
{
int arr[] = {8,3,9,5,6,7,1,4,0,2};
int i = 0;
int len = sizeof(arr) / sizeof(arr[0]);
InsertionSort(arr,len);
for (i = 0;i < (sizeof(arr) / sizeof(arr[0]));i++)
{
printf("%d ", arr[i]);
}
system("pause");
return 0;
}元素集合越接近有序,直接插入排序算法的时间效率越高
最优情况下:时间效率为O(n)
最差情况下:时间复杂度为O(n² )
空间复杂度:O(1),它是一种稳定的排序算法
希尔排序
1959年Shell发明,第一个突破O(n2)的排序算法,是简单插入排序的改进版。它与插入排序的不同之处在于,它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。
如果有两个相对的数字,排序中两个元素可能会交换,所以希尔排序是不稳定算法
- 选择一个增量序列、
- 按增量序列个数k,对序列进行k 趟排序;
- 每趟排序,根据对应的增量ti,将待排序列分割成若干长度为m 的子序列,分别对各子表进行直接插入排序。仅增量因子为1 时,整个序列作为一个表来处理,表长度即为整个序列的长度
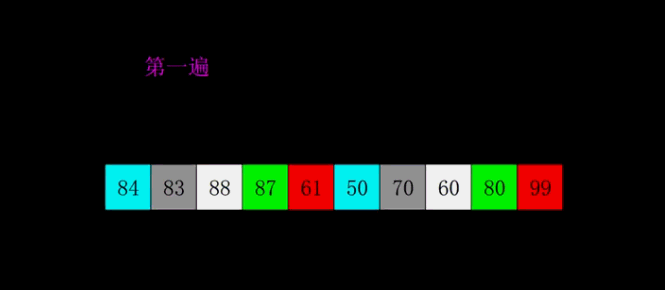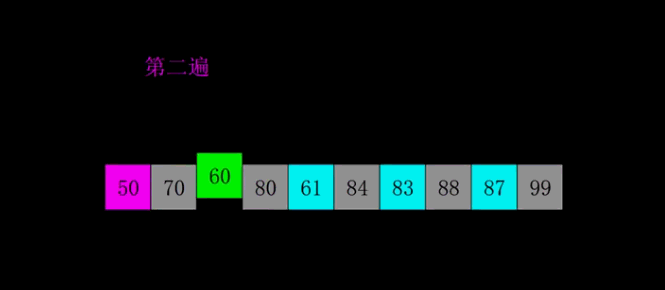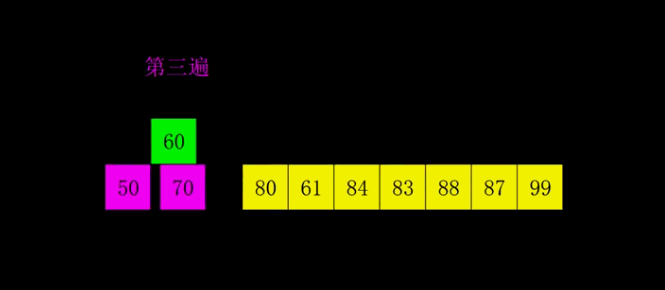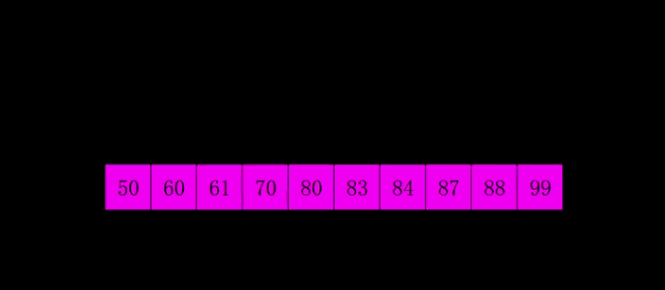
两种对gap的比较排序方式
#include<stdio.h>
#include<stdlib.h>
void swap(int* L, int* R)
{
int temp = *L;
*L = *R;
*R = temp;
}
void ShellSort(int* arr, int len)
{
for (int gap = (len / 2); gap > 0;gap /= 2)//设置gap起始间距为长度的一半
{
//以gap为间距组从一个组,每次对这个组进行直接插入排序
for (int i = gap; i < len;i++)
//以gap位置为起始,找到每一个元素以gap间隔为组向前进行直接插入排序
{
int j = i;
while ((arr[j]< arr[j - gap]) && j - gap >= 0)
{
swap(&arr[j],&arr[j -gap]);
j -= gap;//找到之前所有的成员比较并排序
}
}
}
}
int main()
{
int arr[] = { 8,3,9,5,6,7,1,4,0,2 };
int i = 0;
int len = sizeof(arr) / sizeof(arr[0]);
ShellSort(arr, len);
for (i = 0;i < len;i++)
{
printf("%d ", arr[i]);
}
system("pause");
return 0;
}
#include<stdio.h>
#include<string.h>
void ShellSort(int* arr, int len)
{
for (int gap = (len / 2); gap > 0;gap /= 2)//设置gap起始间距为长度的一半
{
//以gap为间距组从一个组,每次对这个组进行直接插入排序
for (int i = gap; i < len;i++)
//以gap位置为起始,找到每一个元素以gap间隔为组向前进行直接插入排序
{
int j = i;
int temp = arr[j];//将起始位置数字保存
while ((temp < arr[j - gap]) && j - gap >= 0)
{//交换
arr[j] = arr[j - gap];
j -= gap;//找到之前所有的成员比较并排序
}
arr[j] = temp;
}
}
}
int main()
{
int arr[] = { 8,3,9,5,6,7,1,4,0,2 };
int i = 0;
int len = sizeof(arr) / sizeof(arr[0]);
ShellSort(arr, len);
for (i = 0;i < len;i++)
{
printf("%d ", arr[i]);
}
system("pause");
return 0;
}
选择排序
直接选择排序
选择排序(Selection-sort)是一种简单直观的排序算法。它的工作原理:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
- 初始状态:无序区为R[1..n],有序区为空;
- 第i趟排序(i=1,2,3…n-1)开始时,当前有序区和无序区分别为R[1..i-1]和R(i..n)。该趟排序从当前无序区中-选出关键字最小的记录 R[k],将它与无序区的第1个记录R交换,使R[1..i]和R[i+1..n)分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区;
- n-1趟结束,数组有序化了
#include<stdio.h>
#include<string.h>
void SelectionSort(int* arr, int len)
{
int min;//保存当前最小数字下标
for (int i = 0;i < len - 1;i++)
{
min = i;
for (int j = i + 1;j < len; j++)
{
if (arr[min] > arr[j])
{
min = j;
}
}
int temp = arr[min];
arr[min] = arr[i];
arr[i] = temp;
}
}
int main()
{
int arr[] = {8,3,9,5,6,7,1,4,0,2};
int i = 0;
int len = sizeof(arr) / sizeof(arr[0]);
SelectionSort(arr,len);
for (i = 0;i < len ;i++)
{
printf("%d ", arr[i]);
}
system("pause");
return 0;
}
表现最稳定的排序算法之一,因为无论什么数据进去都是O(n2)的时间复杂度,所以用到它的时候,数据规模越小越好。
堆排序
堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序,它的最坏,最好,平均时间复杂度均为O(nlogn),它也是不稳定排序。首先简单了解下堆结构。
堆
堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。如下图:
#include<stdio.h>
#include<string.h>
#include<assert.h>
void AdjustHead(int *arr, int parent, int len)
{//大堆
assert(arr);
int child = parent * 2 + 1;
while (child < len)
{
if (arr[child] < arr[child + 1] && child + 1 < len)
{
child += 1;//左子树小于右子树交且合法时交换
}
if (arr[child] > arr[parent])
{//将大值交给父亲节点
int temp = arr[child];
arr[child] = arr[parent];
arr[parent] = temp;
//复位,再次判断,防止左右孩子都大于双亲
parent = child;
child = parent * 2 + 1;
}
else
return;//不满足退出
}
}
void HeapSort(int* arr, int len)
{
//建堆
int root = (len - 2) >> 1;//找到最后一个非叶子节点
for (root;root >= 0;--root)
{
AdjustHead(arr, root, len);
}
//排序
int end = len - 1;
while (end)
{
int temp = arr[0];
arr[0] = arr[end];
arr[end] = temp;
//循环排序每一个元素
AdjustHead(arr,0,end);
end--;
}
}
int main()
{
int arr[] = {8,3,9,5,6,7,1,4,0,2};
int i = 0;
int len = sizeof(arr) / sizeof(arr[0]);
HeapSort(arr,len);
for (i = 0;i < len ;i++)
{
printf("%d ", arr[i]);
}
system("pause");
return 0;
}
- 将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆,此堆为初始的无序区;
- 将堆顶元素R[1]与最后一个元素R[n]交换,此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n];
- 由于交换后新的堆顶R[1]可能违反堆的性质,因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆,然后再次将R[1]与无序区最后一个元素交换,得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1,则整个排序过程完成。
交换排序
冒泡排序
是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。
算法描述
- 比较相邻的元素。如果第一个比第二个大,就交换它们两个;
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;
- 针对所有的元素重复以上的步骤,除了最后一个;
- 重复步骤1~3,直到排序完成。
#include<stdio.h>
#include<string.h>
void bubbleSort(int* arr,int len)
{
int i, j;
for (i = 0;i < len - 1;i++)
{
for (j = 0;j < len - 1 - i;j++)
{
if (arr[j] > arr[j + 1])
{
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
int main()
{
int i;
int arr[] = {6,3,8,7,5,4,1,2,0};
int len = sizeof(arr) / sizeof(arr[0]);
bubbleSort(arr,len);
for (i = 0;i < (sizeof(arr) / sizeof(arr[0]));i++)
{
printf("%d ", arr[i]);
}
system("pause");
return 0;
}快速排序
快速排序具有最好的平均性能(average behavior),但最坏性能(worst case behavior)和插入排序相同,也是O(n^2)。
比如一个序列5,4,3,2,1,要排为1,2,3,4,5。按照快速排序方法,每次只会有一个数据进入正确顺序,不能把数据分成大小相当的两份,很明显,排序的过程就成了一个歪脖子树,树的深度为n,那时间复杂度就成了O(n^2)。尽管如此,需要排序的情况几乎都是乱序的,自然性能就保证了。据书上的测试图来看,在数据量小于20的时候,插入排序具有最好的性能。当大于20时,快速排序具有最好的性能,归并(merge sort)和堆排序(heap sort)也望尘莫及,尽管复杂度都为nlog2(n)。
1、算法思想
快速排序是C.R.A.Hoare于1962年提出的一种划分交换排序。它采用了一种分治的策略,通常称其为分治法(Divide-and-ConquerMethod)。
分治法的基本思想是:将原问题分解为若干个规模更小但结构与原问题相似的子问题。递归地解这些子问题,然后将这些子问题的解组合为原问题的解。
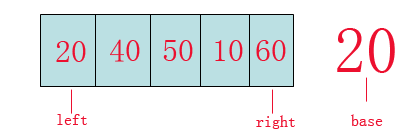
借鉴来源
首先我们从数组的left位置取出该数(20)作为基准(base)参照物。
- 从数组的right位置向前找,一直找到比(base)小的数, 如果找到,将此数赋给left位置(也就是将10赋给20),此时数组为:10,40,50,10,60, left和right指针分别为前后的10。
- 从数组的left位置向后找,一直找到比(base)大的数,如果找到,将此数赋给right的位置(也就是40赋给10), 此时数组为:10,40,50,40,60, left和right指针分别为前后的40。
- 重复“第二,第三“步骤,直到left和right指针重合, 最后将(base)插入到40的位置,此时数组值为: 10,20,50,40,60,至此完成一次排序
- 此时20已经潜入到数组的内部,20的左侧一组数都比20小,20的右侧作为一组数都比20大, 以20为切入点对左右两边数按照"第一,第二,第三,第四"步骤进行,最终快排大功告成
#include<stdio.h>
#include<string.h>
#include<assert.h>
void QuickSort(int* arr,int left, int right)
{
int i = left;
int j = right;
int temp = arr[i];
if (i >= j)
return;
while (i != j)
{
while (arr[j] >= temp && i < j)
{
j--;
}
if (i < j)
{
arr[i] = arr[j];
}
while (arr[i] <= temp && i < j)
{
i++;
}
if ( i < j)
{
arr[j] = arr[i];
}
}
arr[i] = temp;
QuickSort(arr,left,i - 1);
QuickSort(arr, i + 1, right);
}
int main()
{
int arr[] = {8,3,9,5,6,7,1,4,0,2};
int i = 0;
int len = sizeof(arr) / sizeof(arr[0]);
QuickSort(arr,0,len - 1);
for (i = 0;i < len ;i++)
{
printf("%d ", arr[i]);
}
system("pause");
return 0;
}归并排序
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。
- 把长度为n的输入序列分成两个长度为n/2的子序列;
- 对这两个子序列分别采用归并排序;
- 将两个排序好的子序列合并成一个最终的排序序列。
#include<stdio.h>
#include<string.h>
#include<assert.h>
//合并
void Merge(int* arr, int low, int mid, int high)
{
int i = low;//第一组下标
int j = mid + 1;//第二组下标
int k = 0;
int arr2[100] = {0};//临时排序存放序列
//循环判断arr[i]和arr[j]的值,谁小谁放在arr2中
while (i <= mid && j <= high)
{
if (arr[i] <= arr[j])
{
arr2[k] = arr[i];
i++;
k++;
}
else
{
arr2[k] = arr[j];
j++;
k++;
}
}
//当至少一组放完后,剩下的全部按顺序放入arr2(已经有序的数组)
//最后一组元素可能不过正常数量
while (i <= mid)
{
arr2[k] = arr[i];
i++;
k++;
}
while (j <= high)
{
arr2[k] = arr[j];
j++;
k++;
}
//将arr2中的序列复制到arr中
for (k = 0, i = low;i <= high;i++, k++)
{
arr[i] = arr2[k];
}
}
void MergeSort(int *arr, int len)
{
//间隔增加(gap就是一组几个元素)
for( int gap = 1;gap < len;gap = (gap * 2) )
{
int i = 0;
//从间隔gap开始排序
for (i = 0;i + 2*gap - 1 < len;i = i + 2*gap)
{
Merge(arr, i , i + gap - 1 , i + 2*gap - 1 );
}
//当gap大于len的一半时,排序for无法排序的两个子组
if (i + gap - 1 < len)
{
Merge(arr, i, i + gap - 1, len - 1);
}
}
}
int main()
{
int arr[] = {8,3,9,5,6,7,1,4,0,2};
int i = 0;
int len = sizeof(arr) / sizeof(arr[0]);
MergeSort(arr,len );
for (i = 0;i < len;i++)
{
printf("%d ", arr[i]);
}
system("pause");
return 0;
}归并排序是一种稳定的排序方法。和选择排序一样,归并排序的性能不受输入数据的影响,但表现比选择排序好的多,因为始终都是O(nlogn)的时间复杂度。代价是需要额外的内存空间。
非比较算法
计数排序
计数排序又称为鸽巢原理, 操作步骤:统计相同元素出现次数根据统计的结果将序列回收到原来的序列中
计数排序不是基于比较的排序算法,是对哈希直接定址法的变形应用,其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
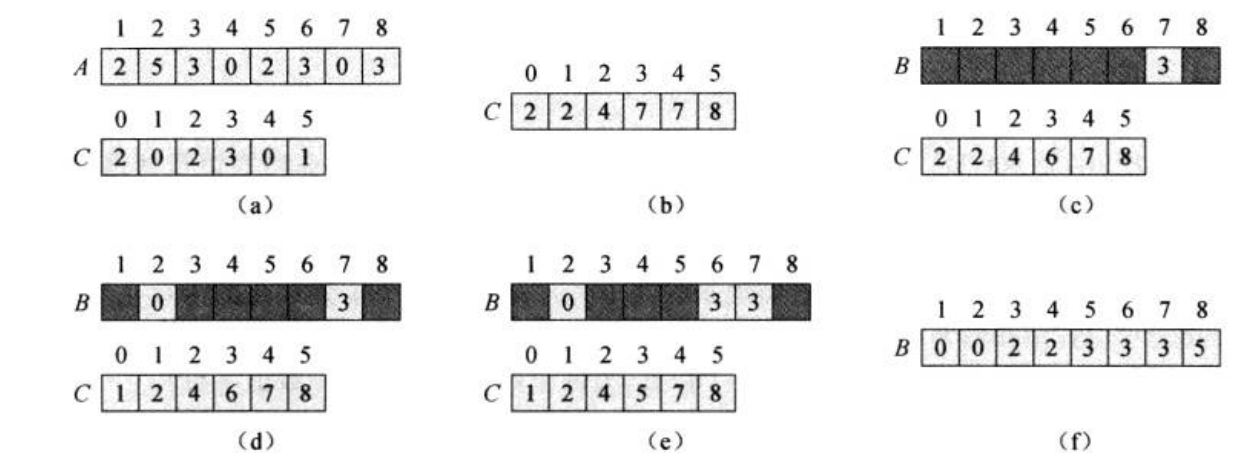
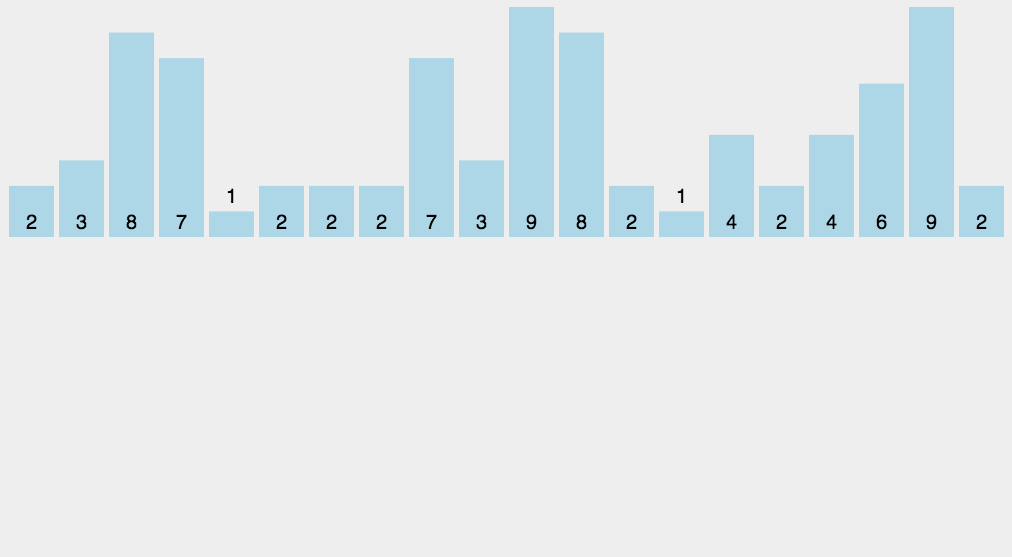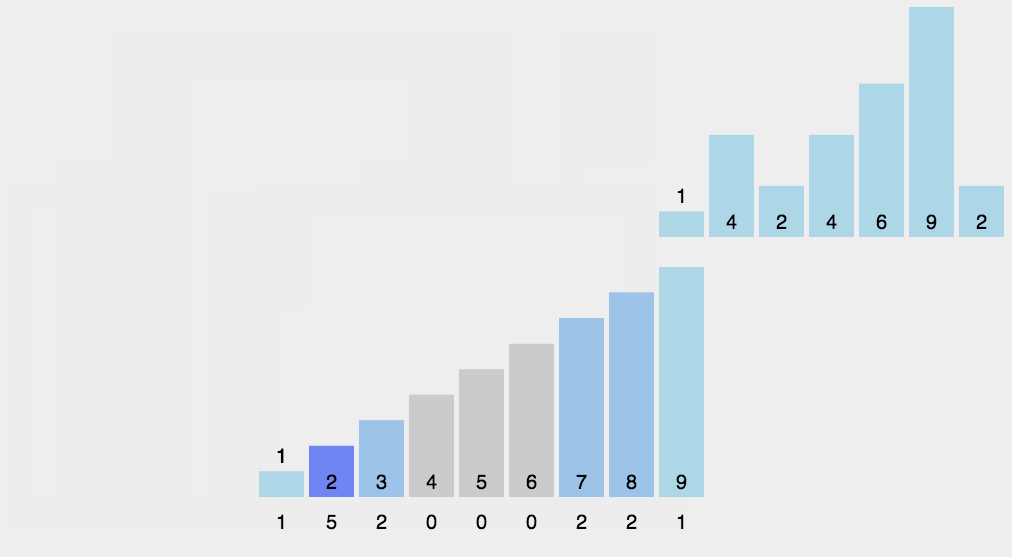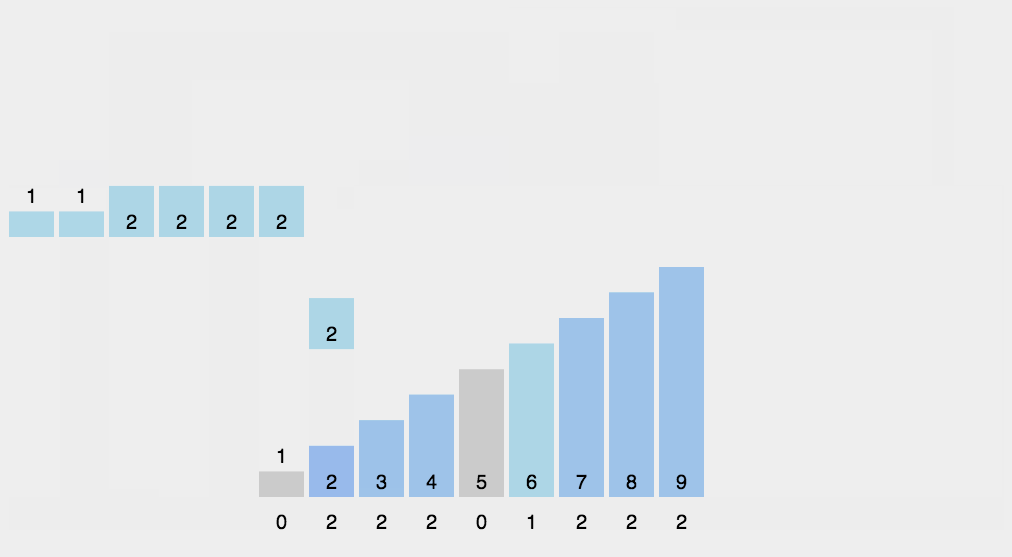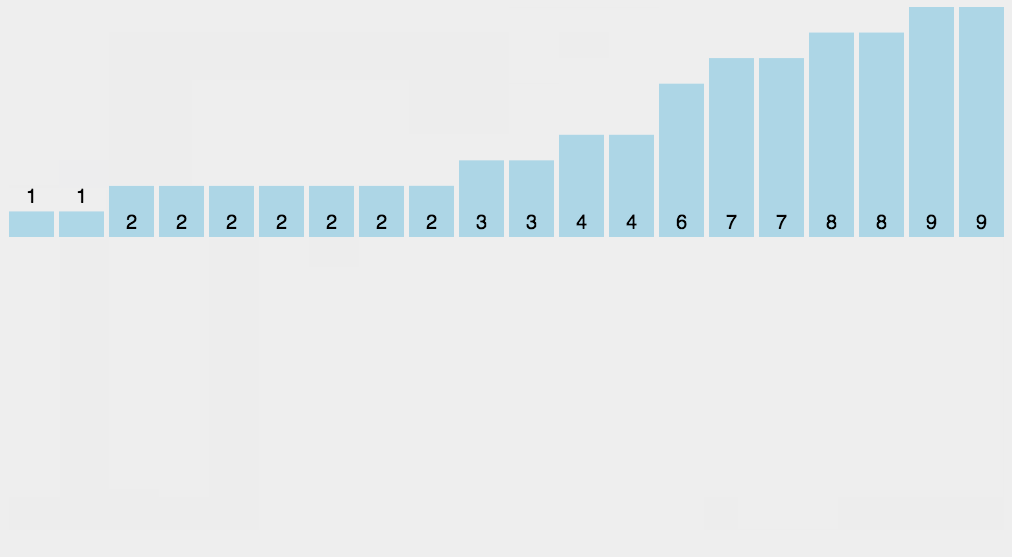
#include<stdio.h>
#include<string.h>
#include<assert.h>
//合并
void CountSort(int* arr, int len)
{
int b[100] = { 0 };
int c[100] = { 0 };
//arr元素必须在100这个范围内
//c的下标是arr的元素,c的内容是arr元素个数
for (int i = 0; i < len;i++)
{
int j = arr[i];//使用数组c对应下标存放
c[j] = c[j] + 1;//arr元素个数
}
//c每两个元素从前到后依次相加,
//因为c中原来存的是元素个数,
//所以现在c数组的元素意义是:
//当前位所代表的元素在b组中的位置
//第几个,没有第零个,从一开始
//所以最后for打印循环i= 1;
//因为初始化置0,所以打印的其余元素都是零
for (int i = 1;i < len;i++)
{
c[i] = c[i] + c[i - 1];
}//确定每个元素位置
for (int i = 0;i < len;i++)
{
//将arr[i]这个元素放在下标对应的数组c内所存的b数组b中的位置
b[c[arr[i]]] = arr[i];
c[arr[i]]--;//元素个数--
}
for (int i = 1;i <= len;i++)
{
printf("%d ", b[i]);
}
}
int main()
{
int arr[] = {8,3,9,5,6,7,1,4,1,2};
int len = sizeof(arr) / sizeof(arr[0]);
CountSort(arr,len );
system("pause");
return 0;
}时间复杂度
| 各种常用排序算法 | ||||||||
| 类别 | 排序方法 | 时间复杂度 | 空间复杂度 | 稳定性 | 复杂性 | 特点 | ||
| 最好 | 平均 | 最坏 | 辅助存储 |
| 简单 |
| ||
| 插入 排序 | 直接插入 | O(N) | O(N2) | O(N2) | O(1) | 稳定 | 简单 |
|
| 希尔排序 | O(N) | O(N1.3) | O(N2) | O(1) | 不稳定 | 复杂 |
| |
| 选择 排序 | 直接选择 | O(N) | O(N2) | O(N2) | O(1) | 不稳定 |
|
|
| 堆排序 | O(N*log2N) | O(N*log2N) | O(N*log2N) | O(1) | 不稳定 | 复杂 |
| |
| 交换 排序 | 冒泡排序 | O(N) | O(N2) | O(N2) | O(1) | 稳定 | 简单 | 1、冒泡排序是一种用时间换空间的排序方法,n小时好 |
| 快速排序 | O(N*log2N) | O(N*log2N) | O(N2) | O(log2n)~O(n) | 不稳定 | 复杂 | 1、n大时好,快速排序比较占用内存,内存随n的增大而增大,但却是效率高不稳定的排序算法。 | |
| 归并排序 | O(N*log2N) | O(N*log2N) | O(N*log2N) | O(n) | 稳定 | 复杂 | 1、n大时好,归并比较占用内存,内存随n的增大而增大,但却是效率高且稳定的排序算法。 | |
| 基数排序 | O(d(r+n)) | O(d(r+n)) | O(d(r+n)) | O(rd+n) | 稳定 | 复杂 |
| |
| 注:r代表关键字基数,d代表长度,n代表关键字个数 | ||||||||
最后
以上就是雪白小蚂蚁最近收集整理的关于数据结构:八大排序理解与C语言实现序插入排序选择排序交换排序 归并排序非比较算法时间复杂度的全部内容,更多相关数据结构内容请搜索靠谱客的其他文章。








发表评论 取消回复