1.递归回溯算法

72 阅读 0 评论 48 点赞

我是靠谱客的博主仁爱月饼，最近开发中收集的这篇文章主要介绍1.递归回溯算法，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

解空间：解空间就是所有解的可能取值构成的空间，一个解往往包含了得到这个解的每一步，往往就是对应解空间树中一条从根节点到叶子节点的路径。子集树和排列树都是一种解空间，它们不是真是存在的数据结构，也就是说并不是真的有这样一棵树，只是抽象出的解空间

算法思想： 在包含问题的所有解的解空间树中，按照深度优先搜索的策略，从根节点出发深度优先搜索解空间树。当搜索到某一节点时，要先判断该节点是否包含问题的解，如果包含就从该节点出发继续深度搜索下去，否则逐层向上回溯。一般在搜索的过程中都会添加相应的剪枝函数，避免无效解的搜索，提高算法效率。

子集树解决问题的时间复杂度为O(2^n)。

例题：给定一组树，打印出这组数中的子集数

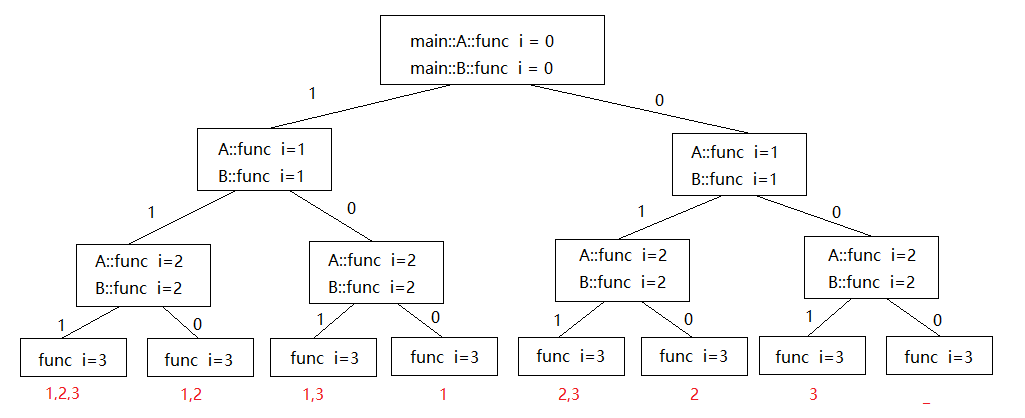
解题思路：可以使用二叉树进行解题，左子树代表被选择的节点，右子树代表未被选择的节点。使用递归回溯遍历整个二叉树。如下图：

#include <stdio.h>
#include <stdlib.h>
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
int arr[] = { 1, 2, 3 };
const int length = sizeof(arr) / sizeof(arr[0]);
vector<int> x;
void func(int i)
{
	if (i == length)//遍历到叶子节点
	{

		for (int j : x)
		{
			cout << j << " ";
		}
		cout << endl;
	}
	else
	{

		x.push_back(arr[i]);
		func(i + 1);//遍历左子树，选择节点 //A
		x.pop_back();
		func(i + 1);//遍历右子树，未选择节点 //B
		
	}
}

int main()
{
	func(0);
	system("pause");
	return 0;
}

结果：