Kmeans均值聚类算法
- Kmeans白话理解
- Kmeans原理详解
- 聚类与分类
- 原理介绍
- 工作流程
- 评价指标
- Kmeans代码实现
- 聊一聊Kmeans的缺点及优化
Kmeans白话理解
Kmeans,又作K-means,顾名思义,K均值聚类算法。Kmeans算法将数据集分为K个簇,使每个簇簇内距离小,簇间距离大。
Kmeans原理详解
聚类与分类
聚类,是将一堆没有标签的数据分成几簇,我们并不关心这一类是什么,我们关心的仅仅只是把相似的目标聚在一起
分类,是将一些给定的打好标签的数据,训练得到某种目标函数,在一个新的数据或者目标出现的时候,对其进行分类,分析它究竟属于哪一类
| 聚类 | 分类 | |
|---|---|---|
| 核心 | 将数据分成簇 | 从已经分组好的数据中训练得出目标函数,把新数据放到已经分好的组中 |
| 学习类型 | 无监督学习 | 有监督学习 |
| 典型算法 | K-means,DBSCAN ,层次聚类,光谱聚类 | 决策树,贝叶斯,逻辑回归 |
| 算法输出 | 聚类结果并不确定,不一定能够反映数据的真实分类,同样的聚类,对于不同的需求,可能好也可能坏 | 分类结果是确定的,分类的优劣是客观的,不根据业务或算法需求而定 |
原理介绍
KMeans算法将一组N个样本的特征矩阵X划分为K个无交集的簇,直观上来看是簇是一组一组聚集在一起的数 据,在一个簇中的数据就认为是同一类。簇就是聚类的结果表现。
簇中所有数据的均值 通常被称为这个簇的“质心”。
工作流程
通俗来讲,
先随机出K个质心,然后按照距离大小,把所有数据点分配给离他们最近的质心,然后我们就有了一簇一簇的数据,一共有K簇。对这些数据取均值,就可以或者新的K个质心,对于这新的K个质心,又可以划分出K个新的簇,如此循环往复,直到算法收敛为止
严谨来讲,
| 步骤 | 过程 |
|---|---|
| 1 | 随机抽取K个样本作为最初的质心 |
| 2 | 根据簇中心对数据进行簇划分 |
| 3 | 重新计算当前簇划分下每个簇的中心 |
| 4 | 在得到簇中心下继续进行簇划分 |
| 5 | 当质心的位置不再发生变化,迭代停止,聚类完成 |
评价指标
inertia指标
又被称为簇内平方和,在统计学中称作“和方差”、“簇内离差平方和”(SSE).inertia表示的是每个样本点到其所在质心的距离之和。显而易见inertia是越小越好。 但实际上当簇数越来越多的时候inertia越来越小。最极端的情况下,簇的数量等于样本数的时候,每一个样本就是一个簇,那么inertia就为0.很难判断什么时候取合适的K比较好
轮廓系数
轮廓系数(Silhouette Coefficient)包含两部分,一部分叫做内聚度,另一部分叫做分离度。内聚度是一个样本点与簇内元素的紧密程度。分离度是一个样本点与簇外元素的紧密程度。
轮廓系数的计算公式如下:
S
(
i
)
=
b
(
i
)
−
a
(
i
)
m
a
x
(
a
(
i
)
,
b
(
i
)
)
S(i) = frac{b(i) - a(i)}{max{(a(i),b(i))}}
S(i)=max(a(i),b(i))b(i)−a(i)
其中,a(i)代表样本点的类内聚度,计算方式如下:
a
(
i
)
=
1
n
−
1
∑
j
≠
i
n
d
i
s
t
a
n
c
e
(
i
,
j
)
a(i) = frac{1}{n-1}sum_{j≠i}^n distance(i,j)
a(i)=n−11j=i∑ndistance(i,j)
其中
j
j
j代表与样本
i
i
i在同一个簇内的其他样本点。
d
i
s
t
a
n
c
e
distance
distance代表了求
i
i
i与
j
j
j的距离。所以
a
(
i
)
a(i)
a(i)越小说明该类越紧密
b
(
i
)
b(i)
b(i)的计算方式与
a
(
i
)
a(i)
a(i)类似。只不过需要遍历其他类簇得到多个值
{
b
1
(
i
)
,
b
2
(
i
)
,
b
3
(
i
)
,
.
.
.
,
b
m
(
i
)
}
{{b_1(i),b_2(i),b_3(i),...,b_m(i)}}
{b1(i),b2(i),b3(i),...,bm(i)},从中选择最小值作为最终结果
当
a
(
i
)
<
b
(
i
)
a(i)<b(i)
a(i)<b(i)时,即类内的距离小于类间距离,则聚类结果更紧凑。S的值会趋近于1。越趋近于1代表轮廓越明显。
相反,当
a
(
i
)
>
b
(
i
)
a(i)>b(i)
a(i)>b(i)时,类内的距离大于类间距离,说明聚类的结果很松散。S的值会趋近于-1,越趋近于-1则聚类的效果越差。
结论:轮廓系数
S
S
S取值范围
[
−
1
,
1
]
[-1,1]
[−1,1],轮廓系数越大聚类效果越好
最后,可以画出K与轮廓系数的折线图,选择轮廓系数最大的K来进行聚类
这部分内容参考:
技术宅zch大佬的博客
https://blog.csdn.net/qq_19672707/article/details/106857918
Kmeans代码实现
数据内容:
二维数据:
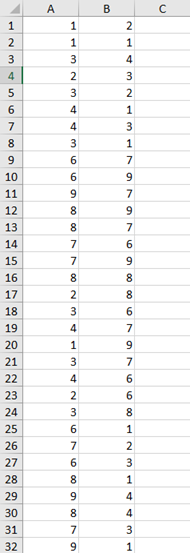
三维数据:
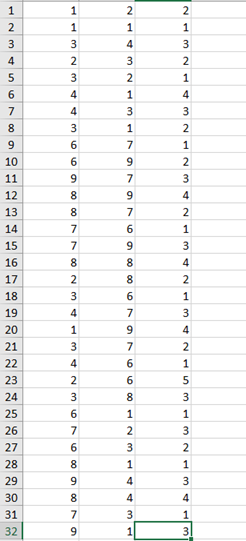 )
)
# 导入第三方模块
import random
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D # 空间三维画图
def load_data(path):
df = pd.read_excel(path)
column_count = df.shape[1]
df_li = df.values.tolist()
return df_li,column_count
# 计算欧式距离,并且存储到数组中
def distance(dataSet,centroids,k):
'''
利用np.tile()将dataSet中的元素扩展到与centroids同一个shape
也就是算出dataSet中的每一个元素分别与centroids的disatcne,
存储到一个列表中,并将这个列表存储到原先设定的空列表中,最后
将存储完数据的列表转换为数组格式
需要明确的是,分成几簇,必定会有k个质心,扩展成k维后,能分别
计算数据集中的某一个元素与这k个质心的距离
'''
dis_list = []
for data in dataSet:
diff = (np.tile(data,(k,1)))-centroids
squaredDiff = diff ** 2
squaredDist = np.sum(squaredDiff,axis=1)
distance = squaredDist ** 0.5
dis_list.append(distance)
dis_list = np.array(dis_list)
return dis_list
# 计算质心,并且返回质心变化量
def Centroids_Init(dataSet,centroids,k):
# 首先计算初始化质心与数据集元素之间的距离
dis_list = distance(dataSet,centroids,k)
# 根据第一次距离计算进行分类,并计算出新的质心
minDistIndices = np.argmin(dis_list,axis=1) #axis 表示每行最小值下标
# #DataFrame(dataSet)对DataSet分组
# groupby(min)按照min进行统计分类
# mean()对分类结果求均值
newCentroids = pd.DataFrame(dataSet).groupby(minDistIndices).mean()
newCentroids = newCentroids.values
# 计算新质心与初始化质心的变化量
centroids_change = newCentroids - centroids
return centroids_change,newCentroids
# 使用K-means进行分类
def k_means(dataSet,k):
# 随机获取质心,作初始化处理
# 从数据集中随机取k个元素作为质心
centroids = random.sample(dataSet,k)
centroids_change,newCentroids = Centroids_Init(dataSet,centroids,k)
# 不断更新质心,直到centroids_change为0,表示聚类中心已经确定
while np.any(centroids_change != 0 ):
centroids_change,newCentroids = Centroids_Init(dataSet,newCentroids,k)
# 将矩阵转换为列表,并排序
centroids = sorted(newCentroids.tolist())
# 根据质心来聚类
cluster = []
# 计算欧式距离
dis_list = distance(dataSet,centroids,k)
minDistIndices = np.argmin(dis_list,axis=1)
for i in range(k):
# 根据k个质心创建k个空列表,表示k个簇
cluster.append([])
for i,j in enumerate(minDistIndices):
# 将dataSet中的元素分类到指定的列表中
cluster[j].append(dataSet[i])
return centroids,cluster
# 数据可视化
def visualization(dataSet,centroids):
if column_count == 2:
for i in range(len(dataSet)):
plt.scatter(dataSet[i][0],dataSet[i][1],marker = 'o',color = 'blue',s = 40,label = '原始点')
for j in range(len(centroids)):
plt.scatter(centroids[j][0],centroids[j][1],marker = 'x',color = 'red',s = 50,label = '质心')
plt.show()
elif column_count == 3:
fig = plt.figure()
ax = Axes3D(fig)
for i in range(len(dataSet)):
ax.scatter(dataSet[i][0],dataSet[i][1],dataSet[i][2],marker = 'o',color = 'blue',s = 40,label = '原始点')
for j in range(len(centroids)):
ax.scatter(centroids[j][0],centroids[j][1],centroids[j][2],marker = 'x',color = 'red',s = 50,label = '质心')
ax.set_zlabel('Z', fontdict={'size': 15, 'color': 'red'})
ax.set_ylabel('Y', fontdict={'size': 15, 'color': 'red'})
ax.set_xlabel('X', fontdict={'size': 15, 'color': 'red'})
plt.show()
else:
print('数据维度过高,无法进行可视化')
if __name__ == '__main__':
path = input(r'请输入文件的路径:')
dataSet,column_count = load_data(path)
print(dataSet)
print('-'*30,'读取成功','-'*30)
k = int(input('请输入簇数:'))
centroids,cluster = k_means(dataSet,k)
print('质心为:%s'%centroids)
print('集群为:%s'%cluster)
visualization(dataSet,centroids)
二维数据运行结果:
运行结果:

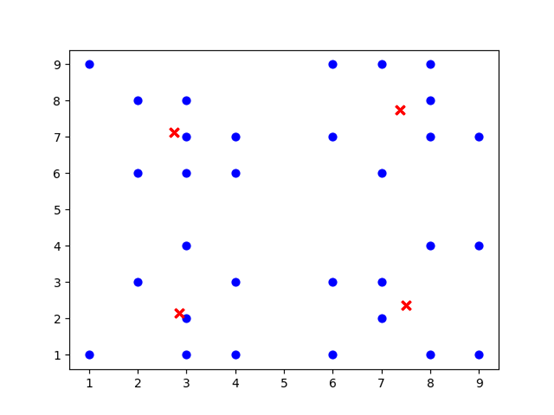
三维数据运行结果:

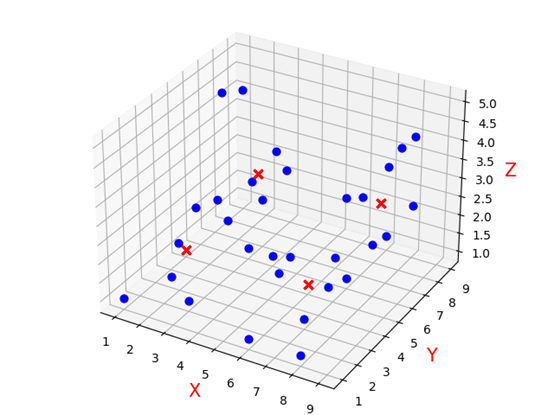
这部分代码从原理上手写一个Kmeans,在真正实战过程中,一般从sklearn中调取Kmeans,这样更简单
聊一聊Kmeans的缺点及优化
Kmeans是很常用的聚类算法,但是如果数据量比较大的时候,计算时间会比较长。所以应运而生的MiniBatchKmeans就是对Kmeans的一种优化。MiniBatchKmeans在尽量保持聚类准确性的情况下,大幅度降低计算时间。
MiniBatchKmeans
1. 首先从数据集中抽取一部分数据,对这部分数据使用Kmeans算法,
2. 然后继续抽取一部分数据,添加进模型,把它们分配给最近的聚类中心
3. 更新聚类中心
4. 循环迭代2和3,直到算法收敛为止
MiniBatchKmeans与Kmeans在聚类的准确性方面相差不大,对于数据量比较大的情况,可以考虑考虑使用MiniBatchKmeans。
关于Kmeans调包操作代码,会在以后的实战过程中记录,欢迎支持!!!
最后
以上就是虚拟西牛最近收集整理的关于Kmeans均值聚类算法的全部内容,更多相关Kmeans均值聚类算法内容请搜索靠谱客的其他文章。








发表评论 取消回复