第五章 Opencv图像的几何变换

几何变换是指改变图像的几何结构，例如大小、角度和形状等，从而使图像呈现出缩放、翻转、仿射和透视效果。

1.缩放图像

1-1.resize()方法

• 语法格式：dst = cv2.resize(src, dsize, fx, fy, interpolation)

• 参数说明：

  • src：原始图像；数组类型。

  • dsize：输出的图像的大小，格式为（宽W，高H），单位为像素；元组类型。

  • fx：可选参数；水平方向的缩放比例。

  • fy：可选参数；垂直方向的缩放比例。

  • interpolation：可选参数；缩放的插值方式。在图像缩小或放大时需要删减或填补像素，该参数可以指定使用哪种算法对像素进行增减；建议使用默认值。

  • dst：输出图像；数组类型。

    注：

    1.resize()方法有两种使用方式，一种是通过dsize参数缩放，另一种是通过fx和fy参数缩放；其中，dsize优先级比fx、fy高。

    2.dsize参数是（宽W，高H）格式，而图像的shape属性是（高H，宽W）格式。

• 实例：

  

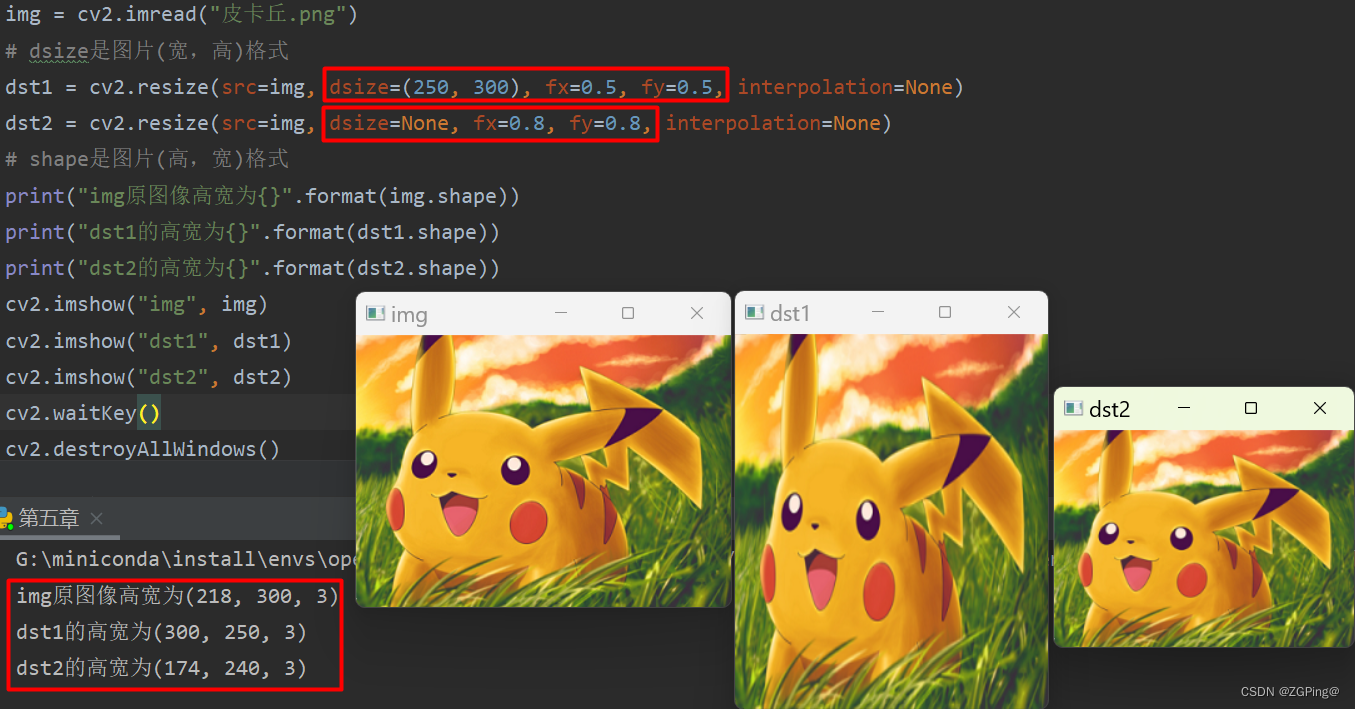
  实例解释：

  1.由dst1和dst2可知dsize优先级比fx、fy高；以及打印的高宽可知dsize参数格式与shape属性格式相反。

2.翻转图像

2-1.flip()方法

• 语法格式：dst = cv2.flip(src, flipCode)

• 参数说明：

  • src：原始图像；数组类型。

  • flipCode：翻转类型。0：X轴翻转；正数：Y轴翻转；负数：先X后Y或者说先Y后X。

  • dst：输出图像；数组类型。

• 实例：

  

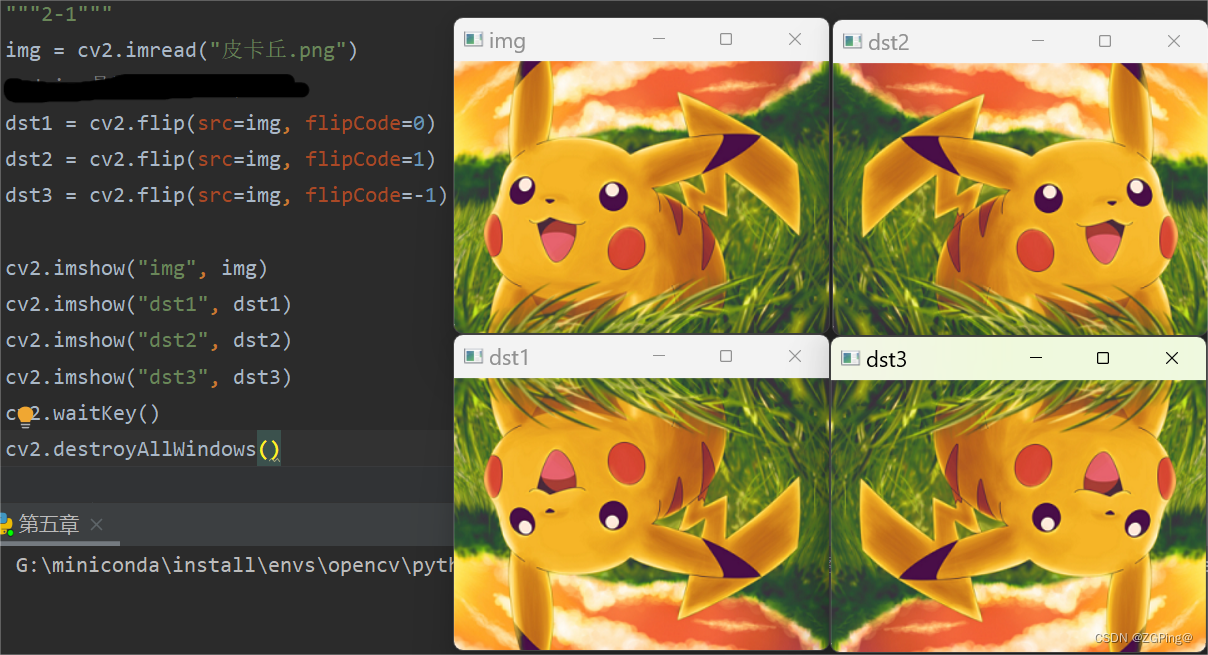
3.仿射变换图像

图像的仿射变换是一种仅在二维平面中进行的几何变形，变换后的图像依然保持直线的“平直性”和“平行性”，即原来是直线的变换后依然是直线，原来是平行线的变换后依然是平行线。常见的仿射变换包括：平移、旋转和倾斜。

3-1.warpAffine()方法

• 语法格式：dst = cv2.warpAffine(src, M, dsize, flags, borderMode, borderValue)

• 参数说明：

  • src：原始图像；数组类型。
  • M：仿射矩阵（是一个2行3列的矩阵）；32位浮点数类型，仿射变换核心就是通过该矩阵进行变换的。
  • dsize：输出图像的大小；单位是像素，默认是原图大小。
  • flags：插值方式；可选参数，建议默认值。
  • boderMode：边界类型；可选参数，建议默认值。
  • boderValue：边界值；可选参数，默认为0用黑色填充，建议默认值。
  • dst：输出图像；数组类型。

• 实例：

  

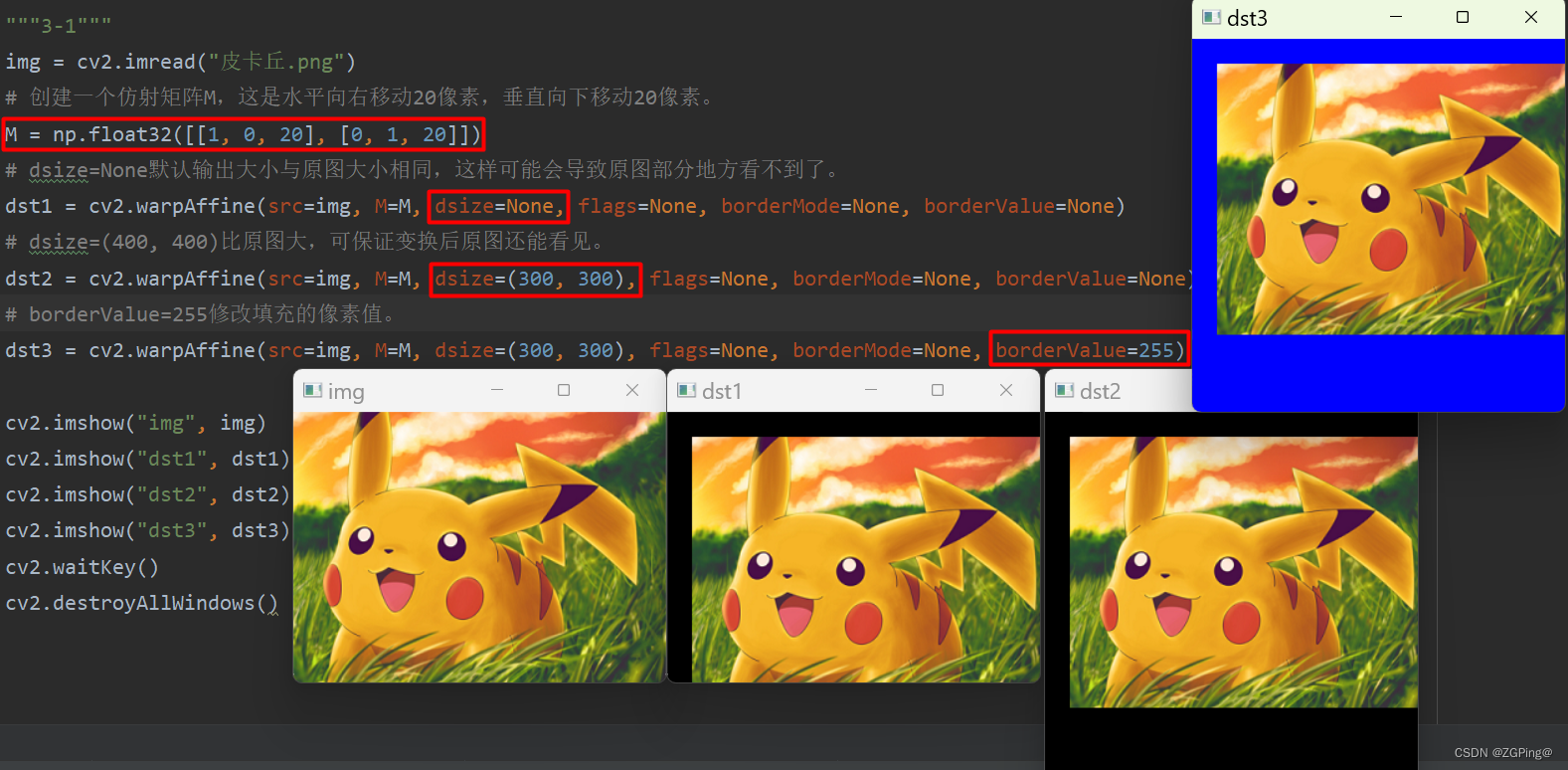
注：

1.仿射变换原理：假设某个像素点坐标为(x, y)，设M = [[a, b, c], [d, e, f]]，该像素点仿射变换后的新坐标为(X, Y)。现在来计算X、Y的值，X = x*a + y*b + c，Y = x*d + y*e + f。

2.平移、旋转和倾斜均利用仿射矩阵来变换，且仿射矩阵为32位浮点数类型。

3-2.平移

• 平移仿射矩阵M：M = [[1, 0, 水平移动距离], [0, 1, 垂直移动距离]]；距离为正数则向右和向下，这和之前讲的像素坐标系中的坐标正负一致。

• 实例：

  看3-1的实例。

3-3.旋转

• 旋转仿射矩阵M：

  由于想要得到旋转仿射矩阵M，需要经过复杂的运算；所以opencv提供了getRotationMatrix2D()方法自动计算出旋转仿射矩阵M。

  • 语法格式：M = cv2.getRotationMatrix2D(center, angle, scale)
  • 参数说明：
    • center：以哪个点作为旋转中心。格式为(W, H)。
    • angle：旋转的角度(单位是°)；整数为逆时针，负数是顺时针。
    • scale：缩放比例，浮点数类型；为1时保持原来的比例。
    • M：旋转仿射矩阵。

• 实例：

  

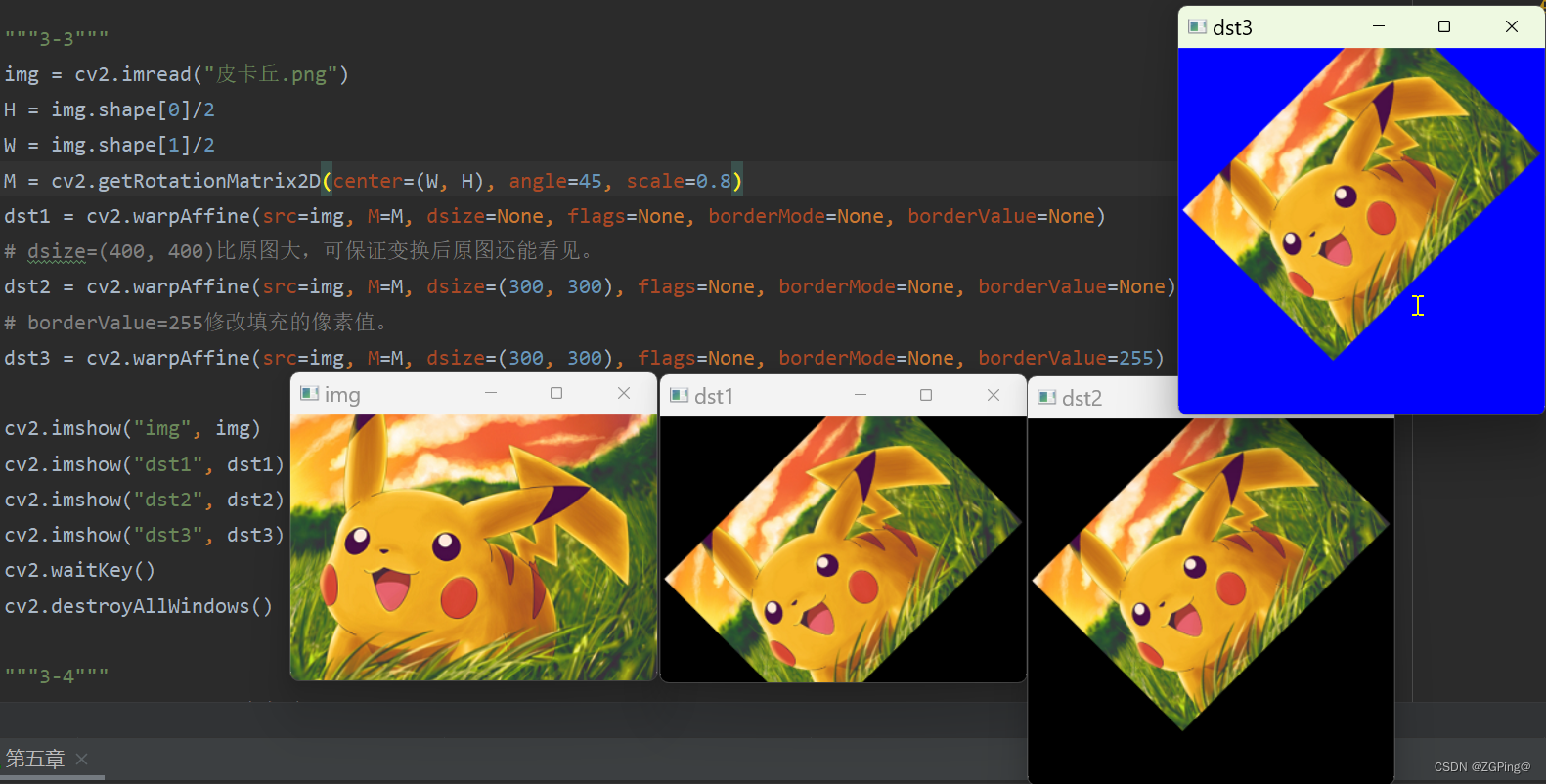
3-4.倾斜

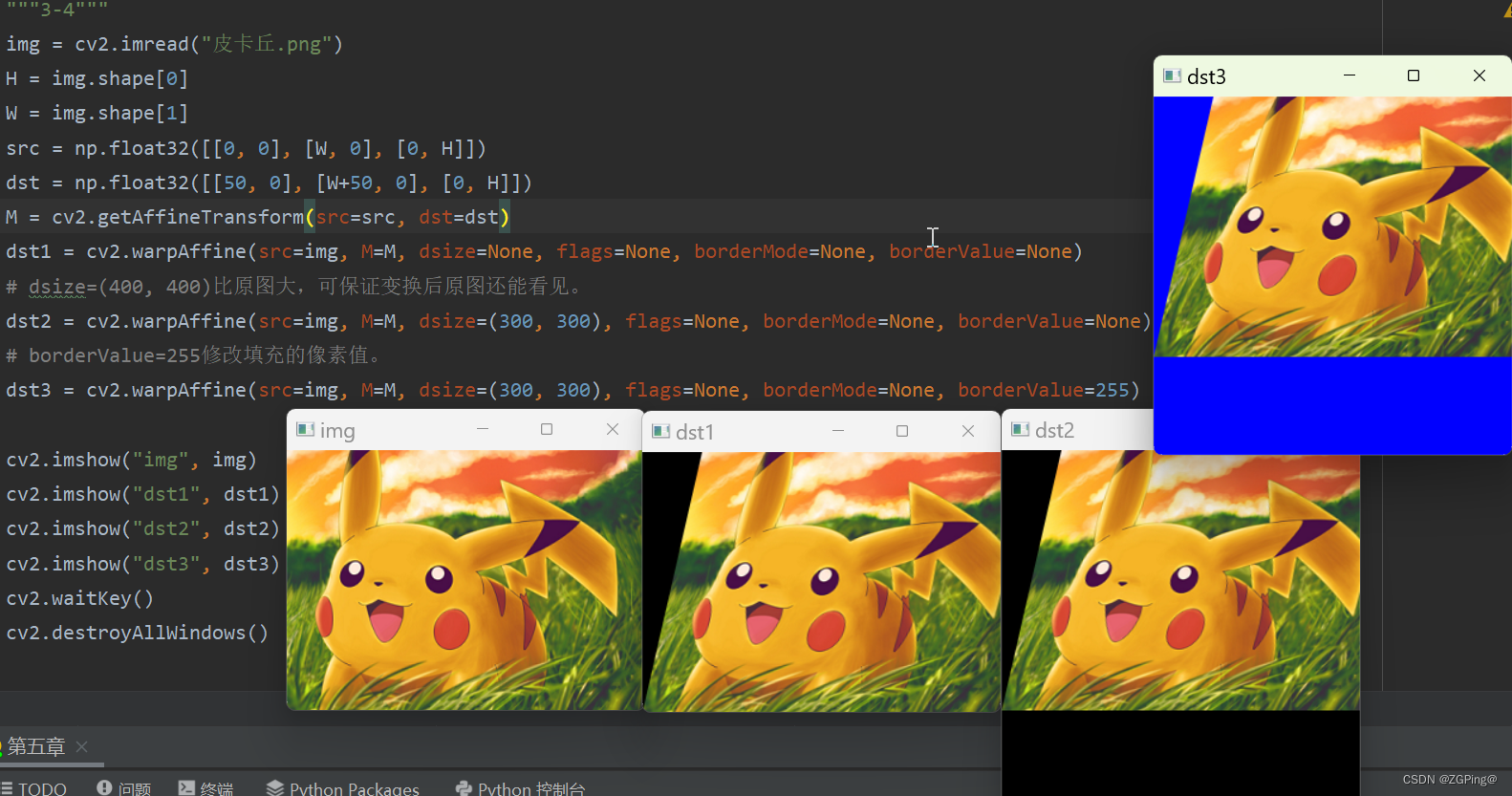
opencv需要至少定位图像的3个点才能实现倾斜效果；3个点的位置类似为矩形的3个顶点，根据这三个点的位置变化计算出其他像素点的位置变化，从而实现图像的倾斜效果。依然满足直线的“平直性”和“平行性”,这也是为什么不需要矩形4个顶点坐标的原因。

• 倾斜仿射矩阵M：

  同求旋转仿射矩阵M，opencv提供了getAffineTransform()方法自动计算出倾斜仿射矩阵M。

  • 语法格式：M = cv2.getAffineTransform(src, dst)
  • 参数说明：
    • src：原图的3个点坐标(宽W，高H)；3行2列的32位浮点数列表，如：[[][][0, 0], [1, 0], [0, 1]]
    • dst：倾斜图像的3个点坐标；格式与src一致。
    • M：倾斜仿射矩阵M。

• 实例：

  

4.透视图像

1.仿射实际上就是将图像在二维空间中变形；而透视就是将图像在三维空间中变形，即改变图像中物体的空间位置。比如：人眼在笔记本电脑某一边看另一边，靠近眼睛的一边会比远离眼睛的对边长，如下图所示。

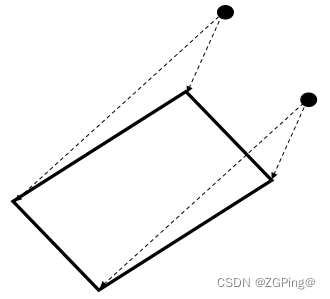
2.opencv至少需要定位图像四个点才能计算透视矩阵M。因此，也就是说是不满足直线的“平直性”和“平行性”，这也是不把它归为仿射变换一类的原因。

4-1.warpPerspective()方法

• 语法格式：dst = cv2.warpPerspective(src, M, dsize, flags, borderMode, borderValue)

• 参数说明：

  • src：原始图像；数组类型。
  • M：透视矩阵（是一个3行3列的矩阵）；也是32位浮点数类型。
  • dsize：输出图像的大小；单位是像素，默认是原图大小。
  • flags：插值方式；可选参数，建议默认值。
  • boderMode：边界类型；可选参数，建议默认值。
  • boderValue：边界值；可选参数，默认为0用黑色填充，建议默认值。
  • dst：输出图像；数组类型。

• 透视矩阵M：

  opencv提供了getPerspectiveTransform()方法自动计算出透视矩阵M。

  • 语法格式：M = getPerspectiveTransform(src, dst)
  • 参数说明：
    • src：原图4个点坐标；格式为4行2列的32为浮点数列表，如：[[0, 0],[1, 0],[0, 1],[1, 1]]。
    • dst：透视图的4个点坐标，格式与src相同。
    • M：透视矩阵

• 实例：

  

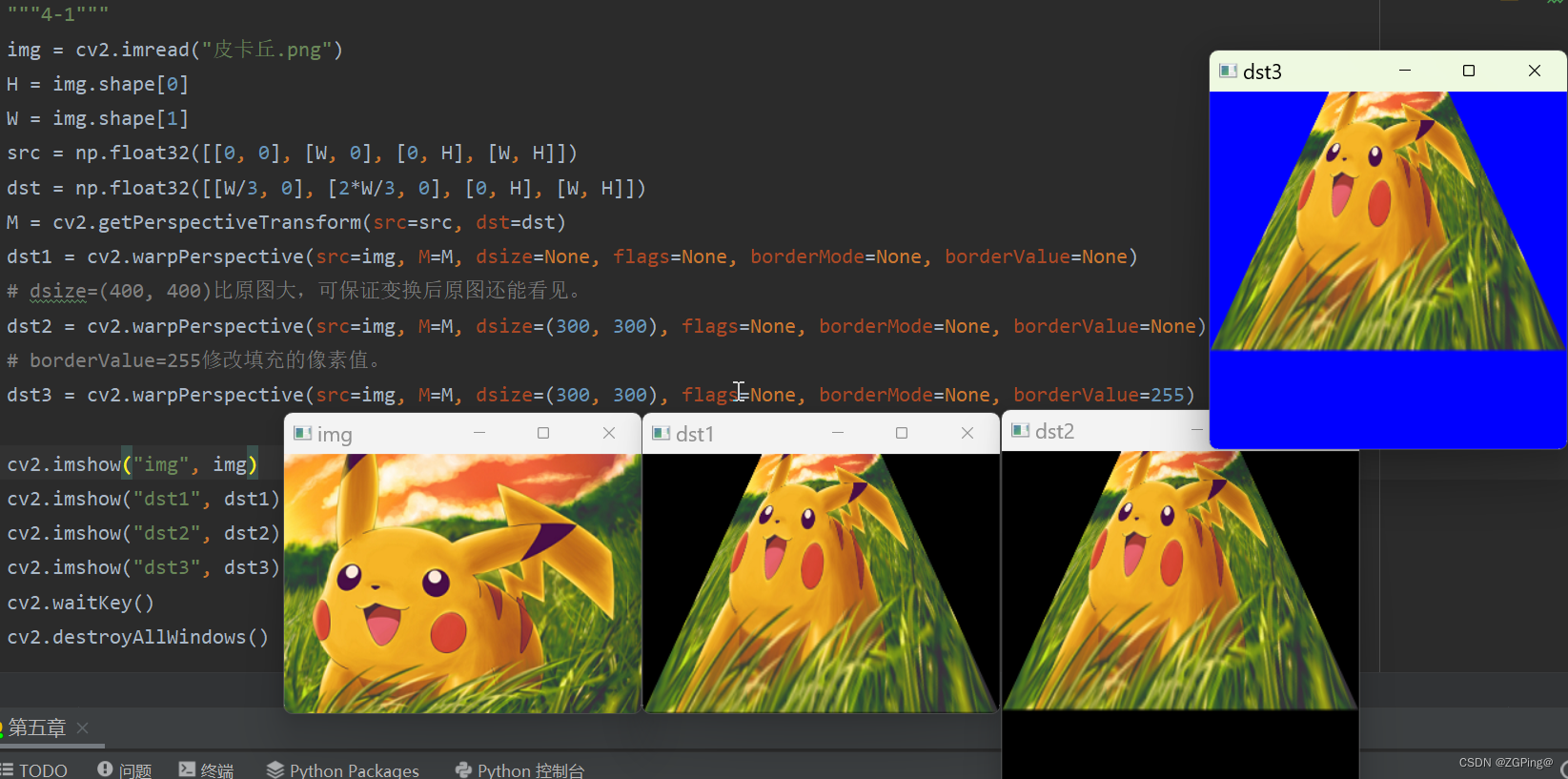
1.非常坑的地方：前面操作像素章节时，像素坐标都是(H, W)的格式；但这里坐标全变成(W, H)格式了！dsize格式也是(W, H)!

最后

以上就是故意天空为你收集整理的第五章 Opencv图像的几何变换的全部内容，希望文章能够帮你解决第五章 Opencv图像的几何变换所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。