时间窗定义
时间窗约束的路径优化问题(VRPTW)是在传统的路径优化(VRP)基础上加入时间窗的约束,时间窗为客户对货物的到达时间必须在规定的 中内到达,其中 为客户 要求送达的最早时间, 为客户 要求送达的最迟时间。如果 与 的值为确定值,则为确定型时间窗,相反,如果 与 的值不确定,则为不确定型时间窗。在现实的运输问题中,很少有客户对于时间的要求是JST(Just In time)模式,即对货物的配送时间有非常严格的要求,大部分的客户对于时间的要求有一定时间弹性。根据时间窗的类型,VRPTW可以分为三类:硬时间窗、软时间窗、混合时间窗。
硬时间窗
硬时间窗(Hard timc windows):为运输车辆必须在客户规定的时间内到达,不允许早到或者晚到,客户只接受在 之间内送达货物,如果是在时间范围外送达货物,早到则需要等待客户,晚到则不接受货物,使得本机运输计划的失败[35]。
如果车辆不能满足时间窗约束,为了更好的体现客户对配送企业的不满便引入了惩罚函数,设定的惩罚函数如下:
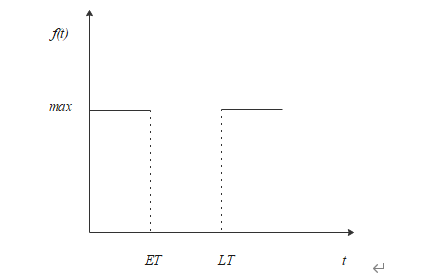
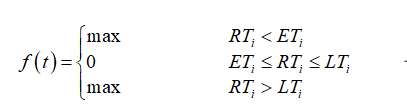
软时间窗
软时间窗(Soft time Windows):相比于硬时间窗,客户对于时间的要求相对松懈一些,即配送车辆在时间窗 内送达没有惩罚,如果没有在规定时间内送达则根据违反时间的长短规定不同的惩罚,以弥补对客户的损失,软时间窗更贴近生活实际,常见的软时间窗下,常见的惩罚函数为线性惩罚,线性惩罚函数如下:
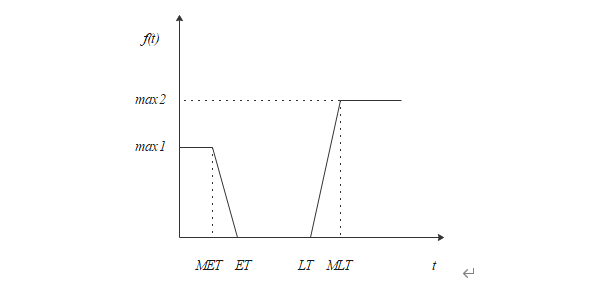
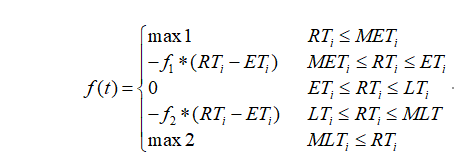
混合时间窗
混合时间窗(Mixed Time Windows):即为有时硬时间窗与软时间窗混合存在,有的客户为硬时间窗,有的客户为软时间窗,这就是混合时间窗。混合时间窗需要区别对待,也就是说不同的时间窗采用不同的惩罚函数[36]。
在现实生活中,存在许多不可控的因素,如道路阻塞、客户要求时间窗不确定等,导致配送车辆无法在客户要求的时间内送达,造成损失。因此,如果是硬时间窗车辆路径问题,那么惩罚成本将过高,不利于企业的盈利,所有物流企业都力求减少成本并尽快将货物送到客户配送中心手中,不会出现偏差过大的情况,而软时间窗VRP,允许配送车辆提前或者是延迟送达,只需要根据违反时间窗的大小支付一定的惩罚费用即可。本设计就为混合时间窗问题
模型假设
在M医药物流有限公司的现状及配送区域、路径优化模型出发,为了将问题转化为数学模型,本设计进行了如下的假设:
(1)配送中心的个数为一个,即起始点的坐标为(0,0),每个配送点的地理位置已知,根据实际距离计算出每个配送点的坐标,并为每个客户依次设置编号;
(2)配送车辆规格已知,车辆类型为单一车型,配送车辆匀速行驶,且配送车辆每次完成配送之后返回初始配送中心;
(3)假设初始配送中心货物齐全,无缺货问题,可以保证每辆配送车辆及时提供,且每次分拣订单都是提前进行,提前准备时间为0;
(4)配送药品无混装禁忌,且药品不能叠层太多,在满足空间、重量的情况下,车辆装载要求为不能超过规定的订单数,没有行驶距离限制;
(5)已知每个客户的每次配送前的需求量,并无临时变动情况,每个订单必须一次配送完成;
(6)已知每个客户的期望服务时间和可接受服务时间,且无临时变动;
(7)不会存在因天气、路况、配送车辆等因素引起的突发问题,初始配送中心到各户的道路始终可行。
参数设置


数学模型

蚁群算法基本原理
蚁群算法是一种寻找路径的概率型算法,由意大利学者Marco Dorigo在蚂蚁寻找食物的路径行为中得到灵感发现的,蚂蚁可以通过信息机制实现信息的传递,能够适应复杂的环境,之后进一步的调查研究发现,信息的传递依靠的是释放的一种被称为“信息素”的物质,蚂蚁通过对信息素浓度强弱的感知,从而去确定要走的路径,路径上信息素的浓度越大,该条路径被其他蚂蚁选择的机会就会更大,这样的过程不断重复,则在最短路径上会有较高的信息素浓度,较长路径上的信息素浓度却会随着时间的流逝而消减,从而蚁群都会逐渐汇聚到最短的路径上各种现象和事物,于1991年总结出相应的规律,首先提出蚁群算法(ant colony optimization, ACO),蚁群算法是一种模拟蚂蚁觅食行为的模拟优化算法并首先使用在解决旅行商问题上,生活中很多看起来高度复杂的问题也就迎刃而解了。
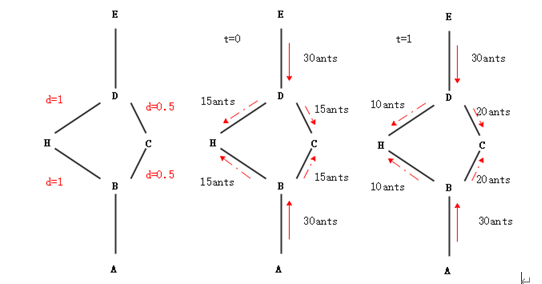
蚂蚁选路示意图,E点代表蚁巢的位置,A点代表食物的位置,蚂蚁从E点出发去往A点寻找食物,在到达D点时,直接到达食物的路径被障碍物阻挡,蚂蚁必须绕开继续前进寻找食物点,此时蚂蚁有两条路DHB和DCB可供选择,假设路径DHB的距离是路径DCB的距离的一倍长度。刚开始两条路上均无被蚂蚁走过,所以不存在信息素,所以一开始蚂蚁选择两条路的概率是相等的,假设有30只蚂蚁,则每条路上的蚂蚁都为15只。在这个过程中,蚂蚁在两条路上均留下信息素,出于路径DHB路程较远,所以信息素浓度较低,蚂蚁走到D点的时候将会有更大的概率选择路径DCB,之后,30只蚂蚁中有10只蚂蚁选择路径DCB,有20只蚂蚁选择路径DHB,这样路径DHB上的信息素浓度将会更高,最终所有的蚂蚁通过这种方式选择出从蚁巢到食物的最短路径。
蚁群算法的特点
1)蚁群算法是一种自组织算法。自组织是来自系统内部的组织,一种不会因为外部条件而改变的一种组织,是一种从无序的过程改变成有序的过程,刚开始单只蚂蚁的选择是随机的不会受到信息素的影响,此为无序,到后边蚂蚁通过之前遗留下的信息素在进行选择的时候就变为有序的过程
2)蚁群算法本质上是一种并行算法。每只蚂蚁的搜索过程彼此独立,互不影响,只通过路径上信息荷尔蒙进行交流。因此,agent colony算法可以看作是一个分布式的agent系统,它同时在问题空间的多个点上开始独立的解搜索,不仅提高了算法的可靠性,而且使算法具有较强的全局搜索能力[38]。
3)蚁群算法是一种正反馈算法。在蚂蚁觅食的过程中不难发现,蚂蚁选择路径的概率依据的是路径上信息素的浓度,浓度越高,选择的几率就会越大,较短路径上就会被更多的蚂蚁经过,留下更多的信息素,从而进一步提高该条路径被下一只蚂蚁选择的概率,这种正反馈使两条路径被选择的概率差距逐渐增加,同时引导整个系统朝最优解的方向发展,正反馈作为蚁群算法重要的特征,使得它对求解路径优化问题成为可能[39]。
4)蚁群算法具有较强的鲁棒性。算法的设置参数少,且在运行的过程中不需要人工的干预,不受初始解的影响,使得蚁群算法适用于更多的优化问题。
蚁群算法数学模型
根据上述对蚁群觅食行为的描述,可知:
1)蚁群算法中包括两种信息素,一种用于蚂蚁去寻找蚂蚁窝,另一种用于蚂蚁去寻找食物位置,并且两种信息素都以一定速率挥发。
2)每个蚂蚁只能感知周围的信息素,当蚂蚁寻找食物时,只能感知自身附近的信息素,假如自身感知范围内存在更浓的信息素和食物,则蚂蚁直接朝食物走去,便不会向信息素更浓的地方走去,蚂蚁可能以小概率进入具有许多信息素的地方。采用不同的方法,这种小概率事件非常重要,它代表着一种寻找方法的创新。找到更好的解决方案非常重要。
3)将蚂蚁归巢的方法与寻找食物的方法相同,都是根据信息素的浓度移动,如果没有信息素的引导,它们将惯性地遵循其运动方向,但是有一定的机会改变方向。蚂蚁还可以记住自己走过的路,以避免重复。
4)蚂蚁在找到食物时会停留一段时间,这样会留下最多的信息素,以便后续蚂蚁更容易找到食物的位置,然后离食物越远,挥发剩余的信息素就越少。蚂蚁在找回巢的方法与寻找食物的方式相同。

流程图
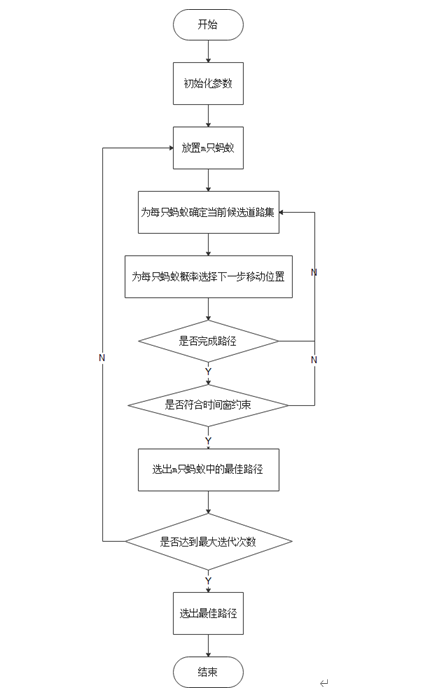
主程序
clear
clc
close all
tic
%% 用importdata这个函数来读取文件
sj=importdata('S1.mat');
dist=importdata('dista.mat');
cap=20; %车辆最大装载次数
%% 是否加急
jj=sj(:,10);
[dx,dx2]=size(sj);
jjjl=[];%加急的另存储
for i=1:dx
if jj(i)==1
jjjl=[jjjl,i];
end
end
%% shuji tiqu
E=sj(1,5); %配送中心时间窗开始时间
L=sj(1,6); %配送中心时间窗结束时间
vertexs=sj(:,2:3); %所有点的坐标x和y
customer=vertexs(2:end,:); %顾客坐标
cusnum=size(customer,1); %顾客数
v_num=2; %车辆最多使用数目
demands=sj(2:end,4); %需求量
a=sj(2:end,5); %顾客时间窗开始时间[a[i],b[i]]
b=sj(2:end,8); %顾客时间窗结束时间[a[i],b[i]]
c=sj(2:end,6);
d=sj(2:end,7);
width=b-a; %顾客的时间窗宽度
s=sj(2:end,9); %客户点的服务时间
cs=35;
% h=pdist(vertexs);
% dist=squareform(h); %距离矩阵
%% 初始化参数
m=50; %蚂蚁数量
alpha=1.5; %信息素重要程度因子
beta=3; %启发函数重要程度因子
gama=0.5; %等待时间重要程度因子
delta=0.5; %时间窗跨度重要程度因子
r0=0.8; %r0为用来控制转移规则的参数
rho=0.9; %信息素挥发因子
Q=8; %更新信息素浓度的常数
Eta=1./dist; %启发函数
Tau=ones(cusnum+1,cusnum+1); %信息素矩阵
Table=zeros(m,cusnum); %路径记录表
iter=1; %迭代次数初值
iter_max=300; %最大迭代次数
Route_best=zeros(iter_max,cusnum); %各代最佳路径
Cost_best=zeros(iter_max,1); %各代最佳路径的成本
%% 迭代寻找最佳路径
while iter<=iter_max
%% 先构建出所有蚂蚁的路径
% 逐个蚂蚁选择
for i=1:m
%逐个顾客选择
for j=1:cusnum
r=rand; %r为在[0,1]上的随机变量
np=next_point(i,Table,Tau,Eta,alpha,beta,gama,delta,r,r0,a,b,width,s,L,dist,cap,demands,cs);
%Tau信息素浓度 Eta启发函数 r随机数 r0为用来控制转移规则的参数
Table(i,j)=np;
end
end
%% 计算各个蚂蚁的成本=1000*车辆使用数目+车辆行驶总距离
cost=zeros(m,1);
NV=zeros(m,1);
TD=zeros(m,1);
for i=1:m
VC=decode(Table(i,:),cap,demands,a,b,L,s,dist,cs);
[cost(i,1),NV(i,1),TD(i,1),~]=costFun(VC,dist,a,s,cs,c,d);
end
%% 计算最小成本及平均成本
if iter == 1
[min_Cost,min_index]=min(cost);
Cost_best(iter)=min_Cost;
Route_best(iter,:)=Table(min_index,:);
else
[min_Cost,min_index]=min(cost);
Cost_best(iter)=min(Cost_best(iter - 1),min_Cost);
if Cost_best(iter)==min_Cost
Route_best(iter,:)=Table(min_index,:);
else
Route_best(iter,:)=Route_best((iter-1),:);
end
end
%% 更新信息素
bestR=Route_best(iter,:);
[~,bestNV,bestTD]=decode(bestR,cap,demands,a,b,L,s,dist,cs);
Tau=updateTau(Tau,bestR,rho,Q,cap,demands,a,b,L,s,dist,cs);
%% 打印当前最优解
disp(['第',num2str(iter),'代最优解:'])
disp(['车辆使用数目:',num2str(bestNV),',车辆行驶总距离:',num2str(bestTD)]);
fprintf('n')
%% 迭代次数加1,清空路径记录表
iter=iter+1;
Table=zeros(m,cusnum);
end
%% 结果显示
bestRoute=Route_best(end,:);
[bestVC,NV,TD]=decode(bestRoute,cap,demands,a,b,L,s,dist,cs);
draw_Best(bestVC,vertexs);
% [~,~,~,ccc]=costFun(bestVC,dist,bestRoute,a,s,cs,c,d)
[~,~,~,ccc]=costFun(bestVC,dist,a,s,cs,c,d)
for i=1:bestNV
bestVC1=cell2mat(bestVC(i));
[arr,~,~,~]=begin_s(bestVC1,a,s,dist,cs)
end
%% 绘图
figure(2)
plot(1:iter_max,Cost_best,'b')
xlabel('迭代次数')
ylabel('成本')
title('各代最小成本变化趋势图')
%% 判断最优解是否满足时间窗约束和载重量约束,0表示违反约束,1表示满足全部约束
flag=Judge(bestVC,cap,demands,a,b,L,s,dist,cs);
%% 检查最优解中是否存在元素丢失的情况,丢失元素,如果没有则为空
DEL=Judge_Del(bestVC);
toc
参数设置
序号 名称 横坐标
(单位:km) 纵坐标
(单位:km)
0 M医药公司 0 0
1 玉田戴家屯药店 -24.8549 14.35
2 鸭鸿桥药店 -21.7508 10.60858
3 九州通药店 -19.9907 23.82398
4 开心大药房 -31.094 27.02963
5 宁心药店 -26.5933 9.67917
6 唐人医药 -27.501 23.07608
7 君康医药 -31.5469 27.42327
8 致远堂 -35.8002 7.609568
9 安康药店1 -46.5578 29.09257
10 安康药店2 -49.2871 29.61469
11 顺德药店 -28.4957 0.497394
12 唐山盛丰医药 -31.1147 20.20611
13 玉田县为民药店 -18.79 28.93413
14 中新药房 -40.985 19.98972
15 民安药房 -29.5373 -3.1045
16 丰润区天青药房 0.331596 18.99711
17 硕东药房 2.461761 20.04943
18 湖岸药房 -3.73141 -2.33164
19 天顺药房 -7.41347 -8.52822
20 同仁堂药店 12.50182 36.30791
21 丰润区敬仁药房 3.813343 27.13335
22 丰润区国成药房 -0.78665 2.161293
23 鑫盛药房 -2.80677 -9.18053
24 润泽药房 -4.91491 -3.44146
25 通和药房 3.459892 32.91867
26 中医医药药房 0.32985 18.89712
27 鸿仁药房 -6.40577 15.85484
28 金卫药房 0.894945 17.07657
29 国康药房 1.75183 20.02351
30 保康药房 -8.60369 7.479073
31 同安药房 0.457183 13.09202
32 分润药房 -14.7847 23.66054
33 文英药房 4.790054 19.21186
34 寿康药房 -7.84619 22.787
35 平价药房 -8.27412 27.06342
在地图中的位置
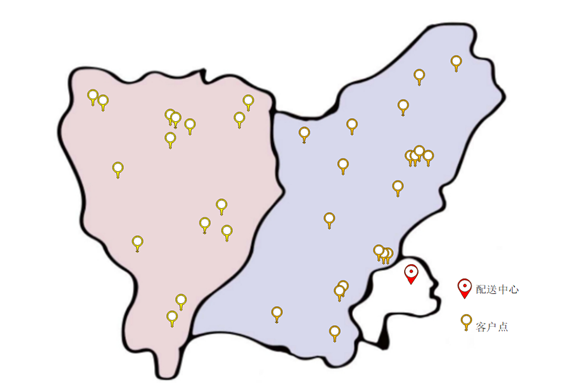
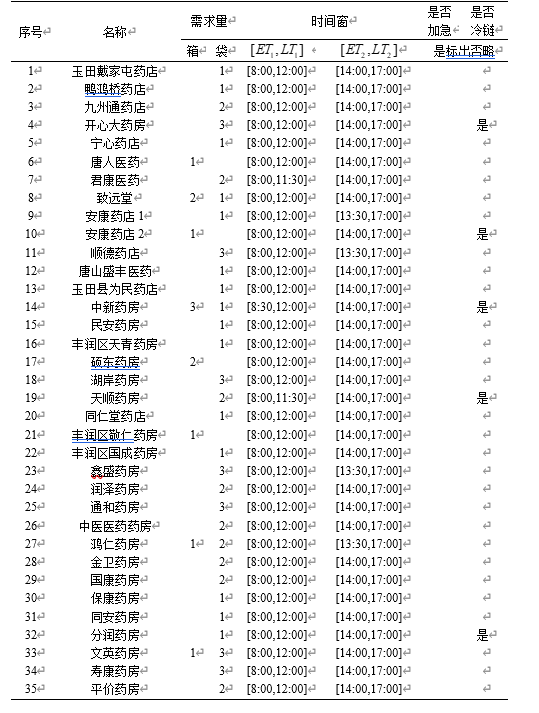
每个客户的订单药品种类多、需求量少需要对每个订单进行装箱、装袋处理,大部分情况下都是进行装袋处理,但是袋在装完药品之后是一个规则的形状,本设计假设袋的长宽高是大部分装满药品的情况下能装下袋子体积最小的长方体的长宽高。需要冷链运输的药品,需求量少采用专门的配送车成本太公,公司采用冷藏箱的方式,将冷藏箱放在配送车中与一般药物共同配送。药品公司各种箱的数据
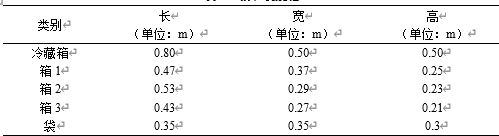
车辆规格

运行结果
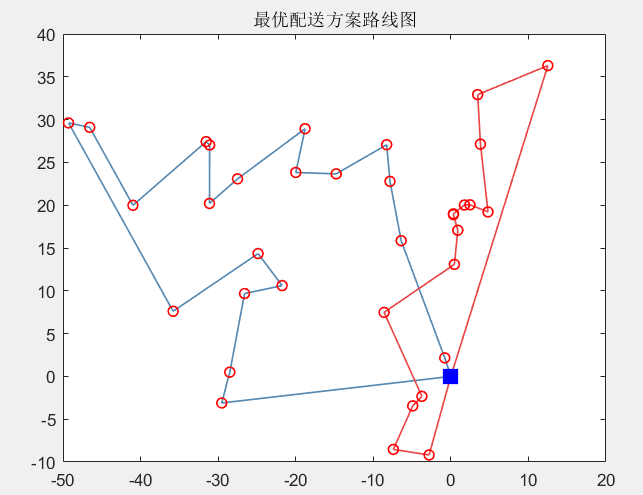
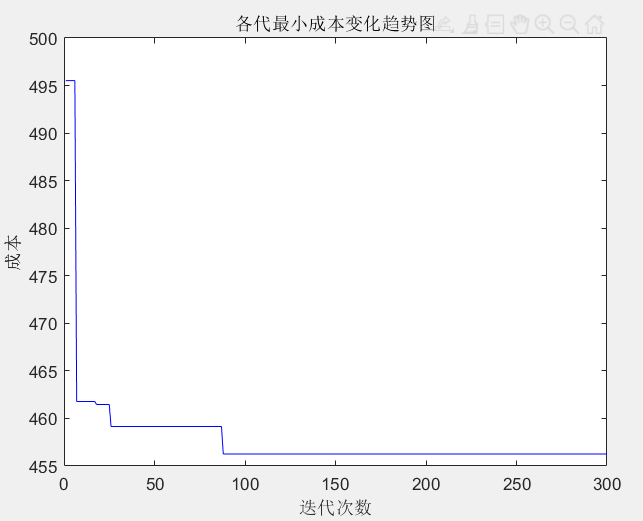
下载地址
如需帮忙V -X:zhangshu2274
最后
以上就是迷你大神最近收集整理的关于matlab蚁群算法求解单车场、有混合时间窗约束、多车辆、非满载的路径优化问题的全部内容,更多相关matlab蚁群算法求解单车场、有混合时间窗约束、多车辆、非满载内容请搜索靠谱客的其他文章。








发表评论 取消回复